三相两电平SVPWM调制策略的研究

2019-09-03李鹏谦何洪军

微特电机 2019年8期

李鹏谦，何洪军

(中国电子科技集团公司第二十一研究所，上海 200233)

0 引言

随着电力电子技术的发展和功率半导体器件制造水平的提高，脉宽调制(以下简称PWM)技术已经成为变频调速领域的核心技术之一[1]。其中，正弦波脉宽调制(以下简称SPWM)较传统PWM技术在输出电压谐波抑制方面有着显著优势，是变频调速领域应用最广泛的PWM技术之一[1-3]。

三相变频器分电流型和电压型两种，根据输入输出形式主要有交-交型和交-直-交型两种类型[1]。其中，以交-直-交型三相电压变频器的应用最为广泛，本文以此拓扑为基础进行SVPWM调制策略的研究。

图1是单极型SPWM调制技术原理。通过计算正弦调制波ur与三角载波uc交点时刻确定开关管的开关时刻，得到一系列等高不等宽并按正弦规律变化的脉冲序列，在调制波正负半周交替处进行倒相操作，得到负半周脉冲序列[4]。双极型SPWM调制属于对称调制，谐波抑制效果较好，电压利用率较单极型SPWM高，具体原理本文不作赘述。

图1 单极型SPWM调制波形

SPWM调制技术在应用过程中仍有不足之处。三相SPWM调制属于三相独立调制，为了降低输出电压谐波含量，通常会选择较高的开关频率，开关损耗较大；其次，电动机在低速时存在明显的转矩脉动现象；最后，SPWM调制技术存在直流电压利用率不高的先天不足，直流电压利用率仅87%左右[5-6]。

20世纪80年代，德国学者提出了空间矢量脉宽调制(以下简称SVPWM)，SVPWM技术可以有效提高直流侧电压利用率，降低低速时的转矩脉动；其次，SVPWM技术可以有效抑制谐波，非常适合DSP等高性能处理器进行数字控制；最后， SVPWM调制过程中每次切换一个H桥开关状态，有效降低了三相H桥的开关损耗。

以三相异步电动机为例，定子侧施加三相电压，合成电压矢量在电机气隙产生圆形旋转磁场，如图2所示。为了有效抑制谐波，降低转矩脉动，对逆变器而言，输出合成电压矢量需要符合旋转磁链轨迹为圆形的调制要求，SPWM技术旨在使逆变器输出电压正弦化，调制效果如上所述并非十分理想。SVPWM调制技术直接以电机运行所需的圆形旋转磁链为调制目标，三相同时控制，同一时刻只有一个桥臂的开关状态切换，性能优异，在磁场定向矢量控制和直接转矩控制领域得到了广泛的应用[7-8]。

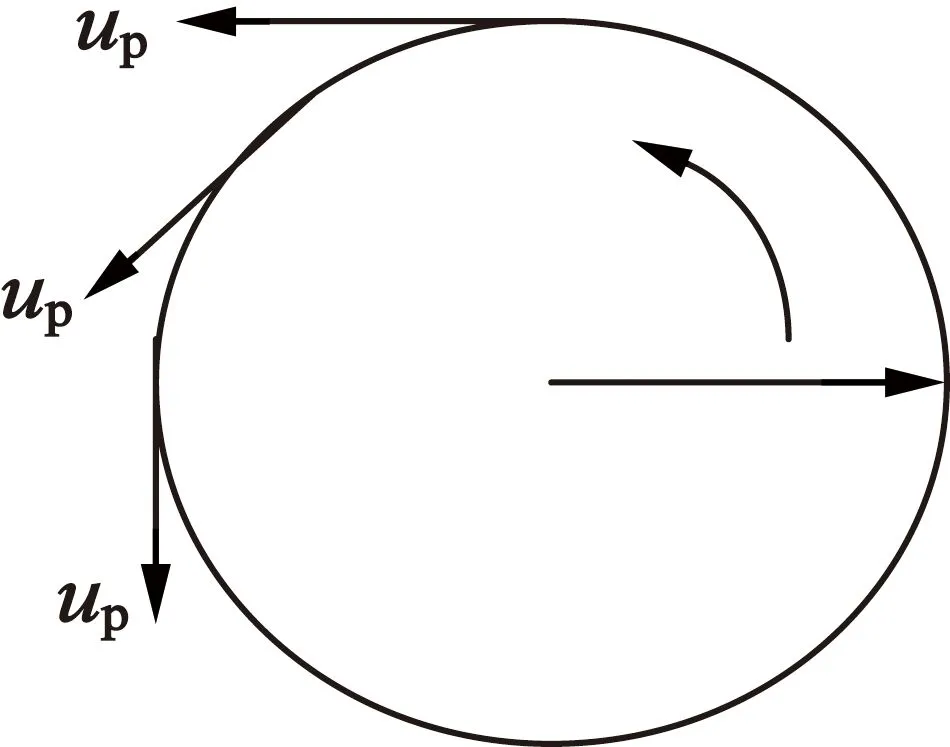
图2 三相异步电动机旋转磁场

1 SVPWM工作原理

1.1 基本空间电压矢量与分布

根据PWM斩波产生电平数的不同，逆变器可分为两电平、三电平和多电平结构，本文讨论的是三相SVPWM调制技术，斩波生成PWM脉冲有直流电压Ud和0两种电平，称为两电平SVPWM调制技术。

图3为三相两电平电压型逆变器拓扑结构。三相星形负载等效三相电机定子绕组，每个H桥上下管互补导通，相位差180°，互补PWM信号设置死区时间，以防止桥臂上下管直通。根据运行状态的不同，图3的逆变器共有8种开关组合，对应不同的逆变器输出电压矢量。

图3 三相两电平逆变器拓扑结构

图4是逆变器运行开关模式示意图。共有8种开关状态：000，001，010，011，100，101，110，111，对应三相逆变器输出的8种电压矢量。其中，000与111状态无有效电压矢量输出，称为零矢量。SVPWM调制过程中，零矢量的插入可以调节输出磁链矢量旋转速度，降低输出谐波分量，抑制转矩脉动。

图4 逆变器运行模式示意图

表1为逆变器开关状态图。

表1 电压矢量开关状态对照图

表1中的8个电压空间矢量分布如图5所示，为空间辐射状。各基本矢量之间依次间隔60°，基本矢量将空间分为6个扇区，按图5中所示，电压矢量进行逆时针切换时电动机是正向旋转的，那么顺时针切换时电动机反向旋转，磁链和合成电压矢量的旋转方向为同一方向。为了便于分析，应用中经常通过等效坐标变换将三相ABC静止坐标系变换到静止正交αβ坐标系中。这种等效变换由之前的三相控制变成两相控制，简化了计算量，易于控制[9]。

图5 电压矢量空间分布示意图

1.2 合成空间电压矢量

由以上分析可知，图3的两电平逆变器有6个有效电压矢量输出，设直流侧电压的参考点为O，星形连接的绕组中性点为O′，记两点电位差为uoo′，逆变器输出到电动机定子绕组的相电压表示如下:

ua=uA-uoo′

(1)

ub=uB-uoo′

(2)

uc=uC-uoo′

(3)

那么，我们得到逆变器输出的合成空间电压矢量:

(4)

这里用函数的方式来表示合成的电压空间矢量:

(6)

基本空间电压矢量u5，它对应的开关状态为001，矢量表达式:

同理，可得其它基本空间电压矢量的矢量表达式，具体计算过程本文不再赘述。

1.3 电压矢量与磁链矢量的关系

图3的逆变器多采用六拍运行模式，每60°切换一次，基本空间电压矢量分布如图5所示，u1～u6是基本电压矢量，可以通过Clarke变换，将三相ABC静止坐标系变换到正交αβ坐标系，α坐标轴与u1重合。

电机学定义，磁链矢量ψ与逆变器电压矢量up的关系有:

(8)

记定子绕组电阻为r，定子电流为i，有:

(9)

忽略r，有:

(10)

忽略初始磁链ψ0，有:

ψ=upΔt

(11)

ψ与up成正比，up旋转一周，沿切线方向旋转2π弧度，因此，对合成磁链的研究可以等效为对逆变器输出合成电压矢量的研究，ψ可用极坐标表示:

ψ=aejθ

(12)

前面提到，三相两电平逆变器采用SVPWM调制策略时多采用六拍切换模式，如图6所示，基本电压矢量u1～u6的连续切换对应磁链ψ5—ψ6—ψ1—ψ2—ψ3—ψ4旋转一周，六拍切换模式简单，但是六拍切换产生的六边形磁链轨迹谐波含量较高，会造成电机绕组发热、转矩脉动等一系列不利影响。

图6 SVPWM调制六拍切换模式

多脉冲法采用多电压矢量连续切换，可以在一定程度上降低六拍切换带来的影响，常见的有18脉冲、30脉冲、42脉冲法等，但每段调制长度不一，控制复杂，计算量大，谐波抑制效果并非十分理想，较少采用。

实际常用引入零矢量的电压矢量合成法进行SVPWM算法调制。将圆周等分为若干段，通过交替切换目标矢量相邻的两个基本矢量来进行等效合成，通过零矢量的插入控制调制度与调制频率，这样可以得到逼近圆形的正多边形磁链轨迹，矢量合成法控制有规律，特别适合DSP进行对称模式调制[1]。

本文采用基于矢量合成法的调制模式进行8段对称模式的SVPWM调制。

2 SVPWM算法调制流程

2.1 静止坐标系变换(3s/2s)

在三相异步电动机的定子绕组中，如采用无中性线的Y型连接方式，定子侧和转子侧各相电流代数和满足：

iA+iB+iC=0

(13)

ia+ib+ic=0

(14)

同时，还满足：

(15)

式中：ψA，ψB，ψC分别为各相磁链分量；LS，LR分别为三相电动机定子侧和转子侧等效电感。

电动机三相数学模型中定子侧各相电压存在如下约束条件：

uA+uB+uC=0

(16)

对于定子绕组采用无中性线Y连接的电动机，三相变量中只有两个参量是自由控制的，三相原始状态下的数学模型并不是物理对象最简单的表达形式，我们可以通过两相模型等效表示三相模型。同时，考虑到矢量控制与直接转矩控制等高性能交流调速策略时，这种由三相模型等效两相模型的变换是常用的。

磁链矢量ψ可以看作是一个自源点出发并在二维空间旋转的矢量，当一个圆形旋转矢量在空间旋转时，它在正交坐标系的横轴与纵轴上的投影分别按照标准正、余弦变化，我们保证α轴矢量以余弦规律变化，β轴矢量以正弦规律变化，那么二者的合成矢量即为圆形旋转矢量，通过三相静止ABC坐标系与正交αβ坐标系的等效变换，完成从三相到两相的控制转化，这样就减少了控制变量，易于控制信号的加载。这里的坐标变换实质上是在保证磁动势平衡的条件下进行相数归算，完成了从三相到两相坐标系的转换，称作Clarke变换。三相静止ABC坐标系与正交αβ坐标系等效变换的示意图如图7所示。

图7 静止坐标系变换

变换过程中满足下式：

(17)

式(17)实现了从三相静止ABC坐标系到两相正交αβ坐标系的变换，减少了控制变量，转换基础是保证磁动势平衡。

2.2 指令信号的产生

指令信号US指希望逆变器输出的电压矢量，此处以极坐标的形式给出，如US=Umeθ，其中，Um为三相输出电压合成矢量的幅值，θ为电压合成矢量的旋转角度，文中未涉及逆变器的反馈控制系统，指令信号可直接在仿真模型中给出。

本文在MATLAB Simulink里面给出三相标准正弦信号作为标准波形，也就是信号波形，对此信号进行坐标变换等操作，经过SVPWM调制生成的PWM脉冲信号对各开关管的开关动作进行控制，通过对三相星形负载的输出电压进行测量判断，以此来判断调制过程的正确性。实际工程中，指令信号的给出远非这么简单，其中涉及到了复杂的控制理论与运算，我们在本文中不作考虑，只做基本理论的分析与实现。

2.3 判断指令所在扇区

获取指令信号后进行SVPWM调制的第一步是要判断指令信号所在的扇区，然后选择基本矢量完成指令信号矢量的合成，三相两电平电压型逆变器的指令信号扇区判断方法如下：

Uα=Umcosθ

(18)

Uβ=Umsinθ

(19)

N=A+2B+4C

(20)

2.4 各基本矢量作用时间计算

指令信号矢量由2个有效矢量和零矢量合成，根据对称性与重复性计算得到电压基本矢量作用时间的基准时间参数，有：

(21)

式中：Ud是直流母线电压；T是各开关管的开关周期。式(21)计算出了矢量作用时间的基准值，各个扇区矢量作用时间如表2所示。

表2 矢量作用时间

表2列出了各个扇区基本矢量作用时间的分配情况，这是生成SVPWM开关信号的重要基础。分析表2可以知道，调制过程中可能出现超调现象，即目标信号矢量的幅值超过了最大直流侧电压幅值允许输出量的现象。因此，在基本矢量作用时间的分配上就会出现T1+T2>T的情况，此时应杜绝这种现象的产生。出现超调时，应根据下式重新进行基本作用时间分配：

(22)

(23)

2.5 矢量切换的分配与实现

计算出各个矢量作用时间后，就要进行各个矢量作用点切换时刻的分配。调制过程中，每一时刻只有一个桥臂的开关管动作，这样可以抑制电压跳变。SVPWM调制方法有多种，本文选择经典的八段对称调制策略，分析每个扇区电压基本矢量的切换规律，如图8所示。

图8 电压矢量位于第1扇区时的切换规律

表3为目标矢量位于各个扇区时的开关切换顺序。这种开关顺序决定了每次只切换一个桥臂的开关导通状态，可以在一定程度上降低电压跳变，同时也降低了开关损耗，这也是空间矢量调制算法的优点之一。

表3 切换顺序表

3 仿真与实验验证

MATLABSimulink仿真平台在电力电子领域的应用非常广泛[10]。本文基于Simulink平台搭建SVPWM调制仿真电路模型，如图9所示，完成了空间矢量调制SVPWM算法的指令信号生成、三相静止ABC坐标系到两相静止αβ坐标系变换、扇区判断、基本时间变量计算、SVPWM信号生成、脉冲分配、主电路搭建等工作。通过测试调整设置观测示波器，可以观测SVPWM调制波形，来分析SVPWM调制机理。