压电驱动平台的自适应PID控制

曾佑轩，马 立，钟博文，孙立宁，汪文峰

(1.上海大学,上海 200072;2. 苏州大学,苏州 215021)

0 引 言

压电陶瓷能够将电能转换成机械能,广泛应用于扫描电子显微镜(SEM)观测、微/纳操作系统、集成芯片制造、生物技术等领域[1-3]。传统的微位移驱动平台无法满足纳米级高精度的运动定位需求,压电驱动平台具有体积小、高能量密度、高分辨率、快响应速度的优点,克服了传统驱动平台的不足,已成为精密定位系统中重要的定位及驱动元件[4-5]。

为了满足对精密产品日益增长的需求，对压电陶瓷精密定位的研究就显得越来越重要[6-8]。虽然现有的前馈PID控制速度快,但是前馈逆模型计算复杂,难以求逆模型,PID参数整定困难,难以满足不同平台的控制需求[9]。随着系统状态的变化，压电陶瓷自适应闭环控制算法可以实现在线实时调整PID参数[10-11]。

1 压电驱动平台前馈PID控制算法

1.1 压电驱动平台驱传动系统建模

在压电驱动平台系统中,以压电陶瓷作为运动的载体，以柔性铰链作为传动机构，从而实现压电驱动平台的运动。首先，对该平台的传动和驱动部分进行动力学分析，结合压电陶瓷的机理，建立如图1所示的等效动力学模型。

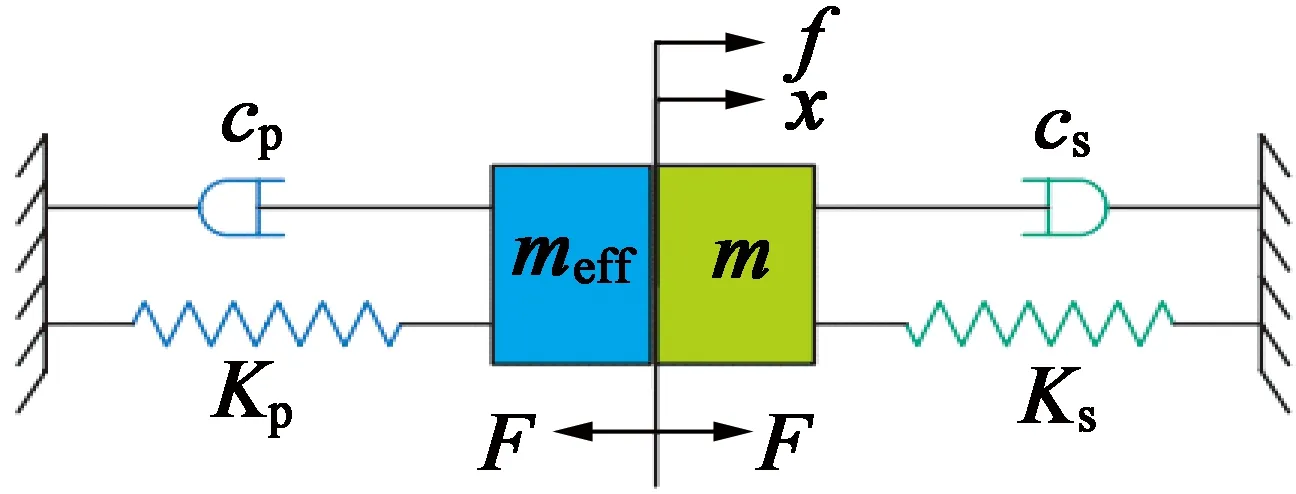
图1 驱动平台的动力学模型

图1中,左边是陶瓷的等效模型,右边是铰链机构的模型;meff和m分别为陶瓷和铰链的等效质量,cp和cs分别为陶瓷和铰链的阻尼系数,Kp和Ks分别为陶瓷和铰链的刚度。F为预紧力,x为位移,f为陶瓷在电压下的驱动力。

驱动传动系统传递函数如下:

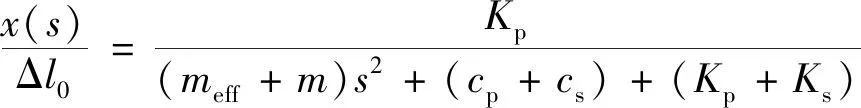
(1)

式中：Δl0为无负载时压电陶瓷的位移。

1.2 遗传算法PID参数整定

根据驱动传动系统传递函数,利用式(2)得出最优参数指标:

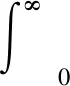
(2)

式中:u(t)是控制器输出；e(t)是系统误差；tu为上升时间；w1，w2，w3为权值；w1=0.999,w2=0.001,w3=2.0。在遗传算法中，当使用的种群个数为30时,可以得到变异概率和交叉概率分别为0.033和0.9。经过100次迭代,代价函数达到目标。PID参数：kp=0.926 4,ki=0.249 2,kd=0.441 6。图2(a)和图2(b)分别为优化代价函数J过程和阶跃响应采用整定后的PID控制的效果[12]，图2(c)为代价函数优化目标。

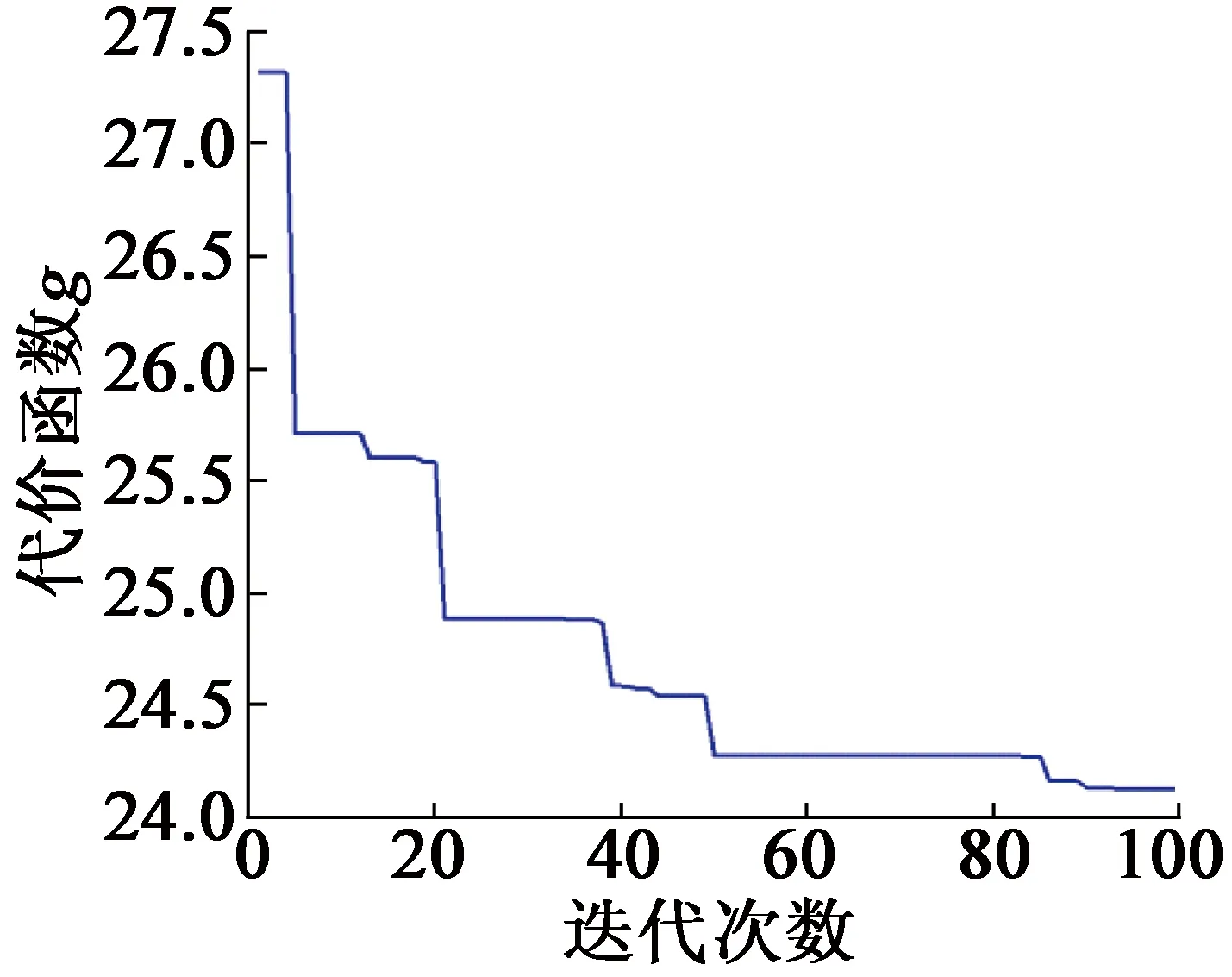
(a) 代价函数的优化过程

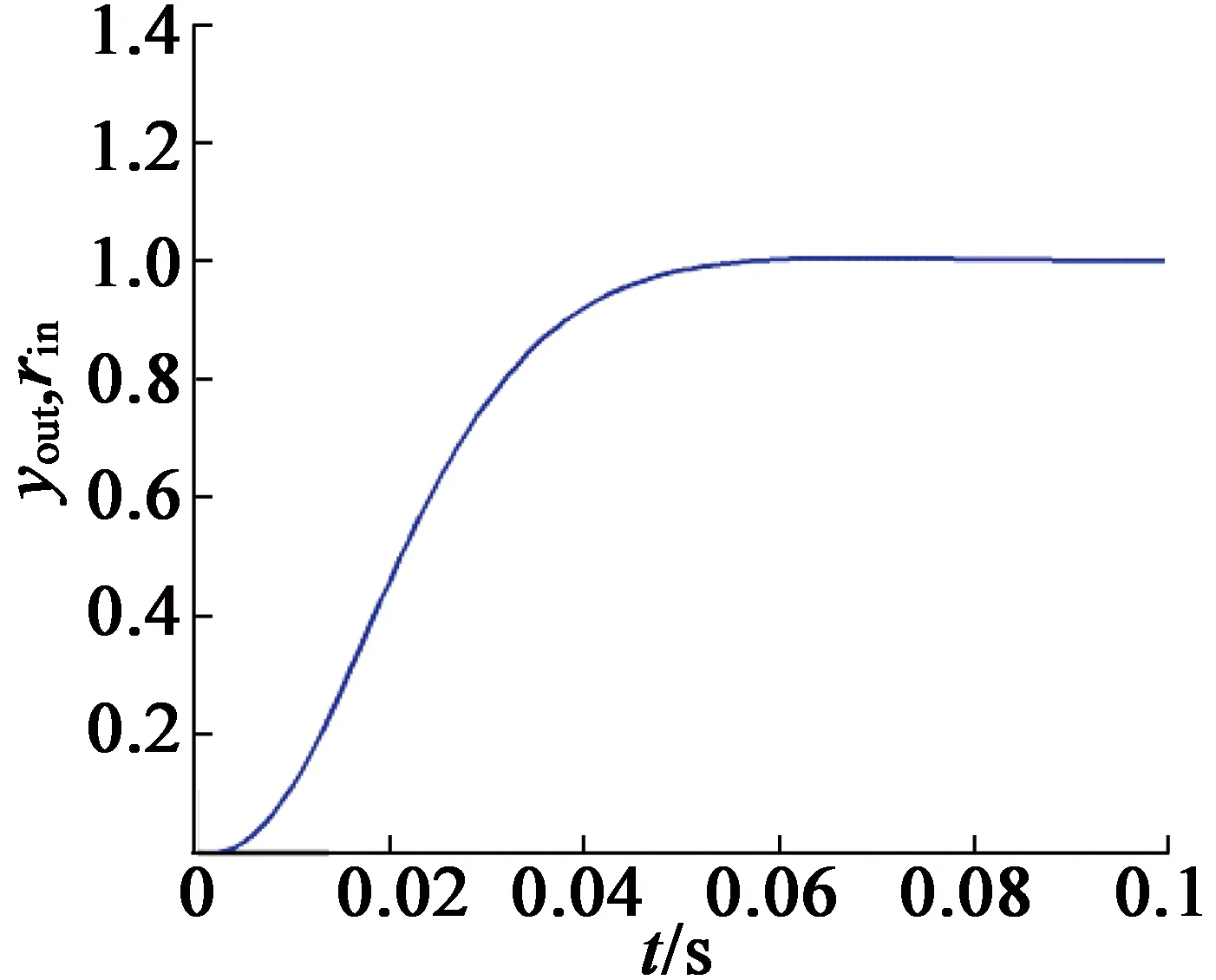
(b) 整定后的阶跃响应曲线

(c) 种群PID参数的优化过程

1.3 非对称PI迟滞模型的改进

针对压电驱动平台迟滞现象所带来的非对称性问题，改进非对称PI迟滞模型如下：

(3)

输入电压增大时，权值为wpj,下降权值wqj为0；输入电压减小时权值为wqj,上升权值wpj为0；F[x(t),y(t),r]为Play算子;z(t)为迟滞模型的输出。

经过MATLAB仿真得到改进后PI迟滞模型的拟合曲线和经典PI迟滞模型的拟合曲线，如图3所示。由图3可以看出,改进非对称PI迟滞模型的拟合值在下降阶段拟合比经典PI迟滞模型误差小[6]。经典PI迟滞模型最大拟合误差为159.5 nm,改进的PI迟滞模型最大拟合误差为66.9 nm。

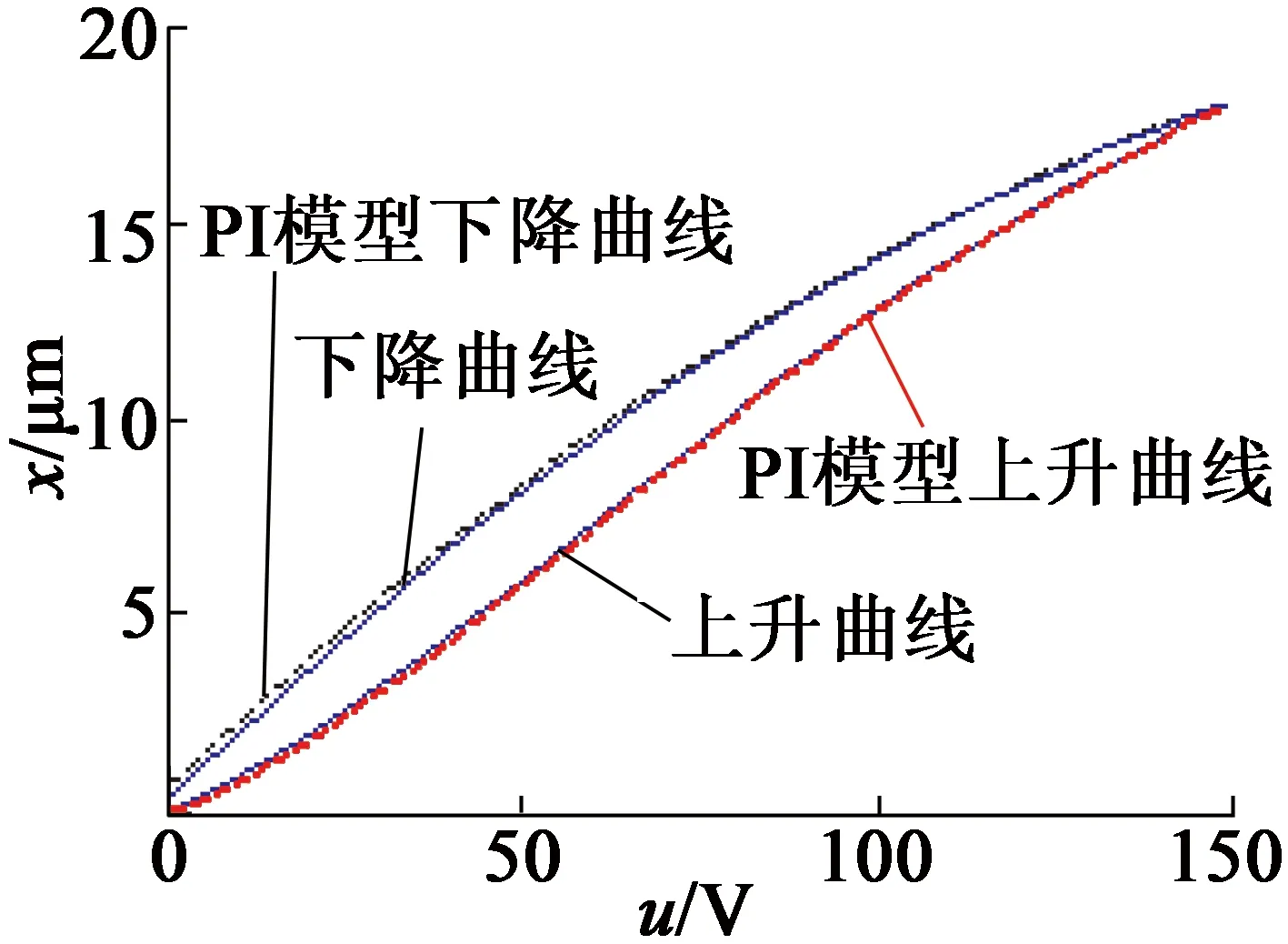
(a) 经典PI迟滞模型拟合

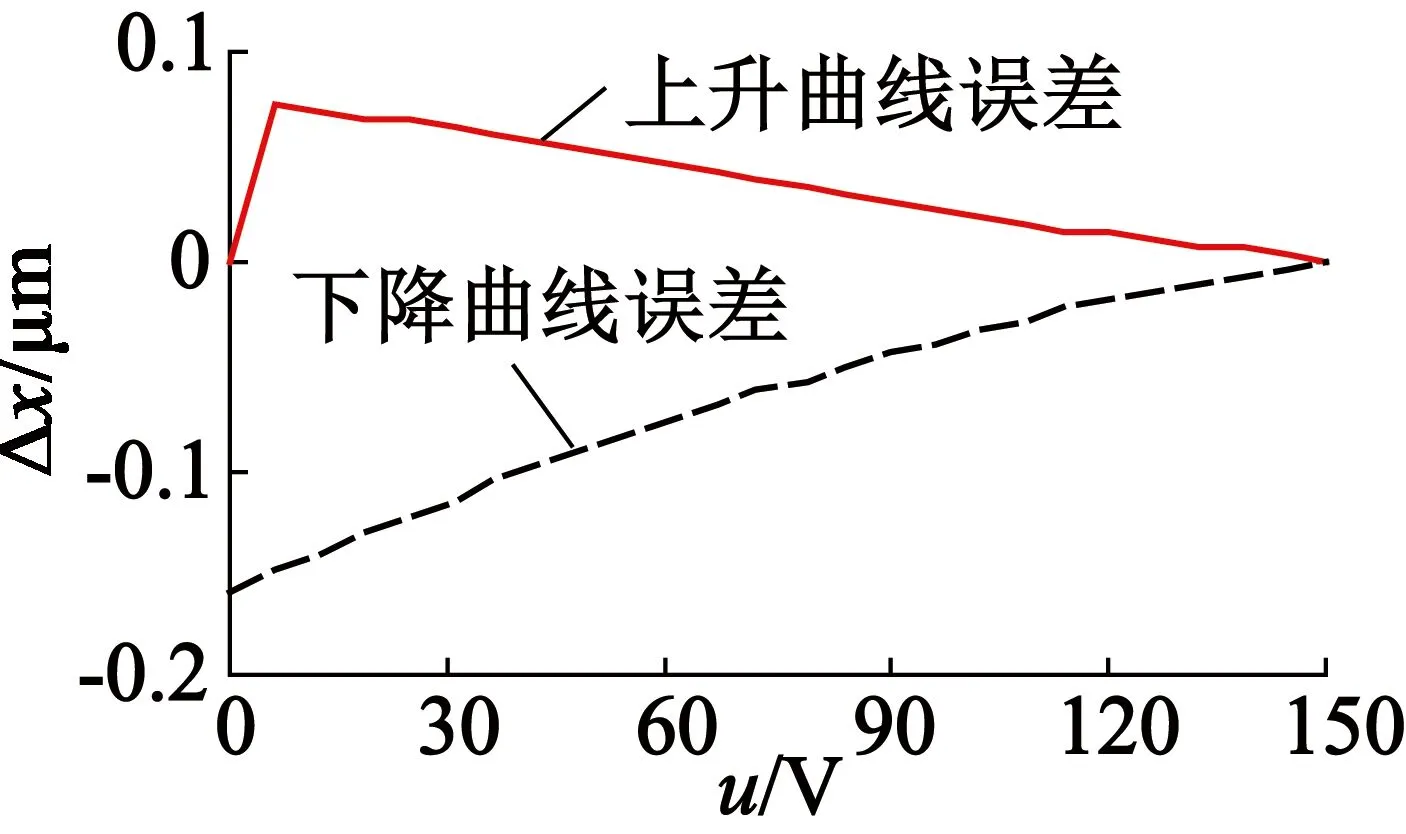
(b) 经典PI迟滞模型拟合误差

(c)改进非对称PI迟滞模型拟合

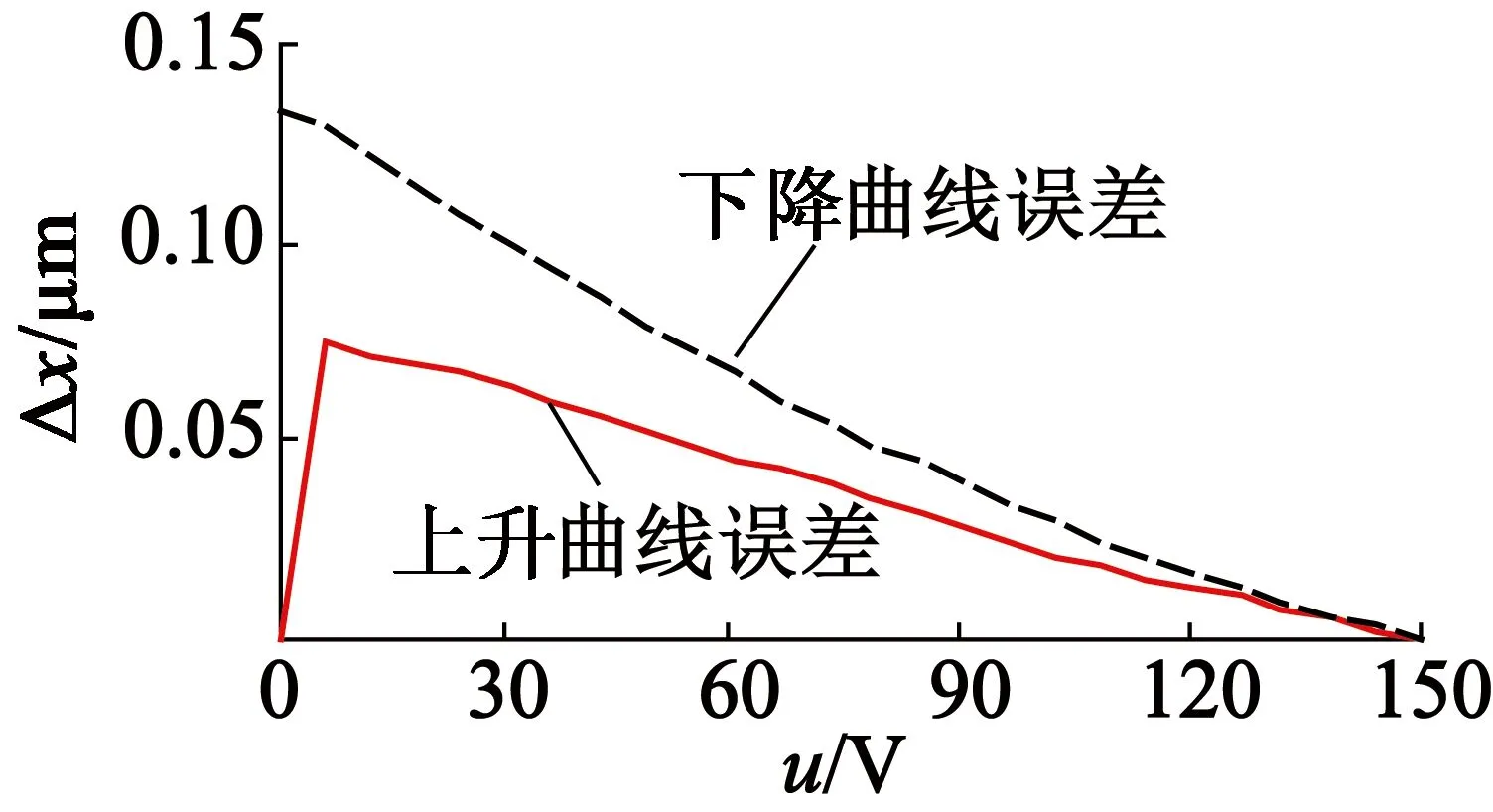
(d) 改进非对称PI迟滞模型误差

图3PI模型拟合及误差

1.4 基于改进PI模型的前馈PID控制

基于PI模型比较容易求逆的优点，式(3)的逆模型可记作如下：

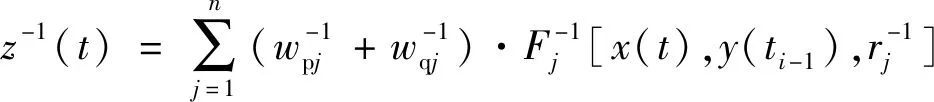
(4)

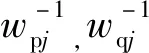
结合PID反馈控制的控制策略，采用基于改进的PI逆模型前馈,得到如图4所示的控制原理图。在整个系统中，首先要根据期望位移值r(t),然后结合前馈模型获得相应的期望电压u(t),最后通过PID反馈控制对压电驱动平台进行误差消除。

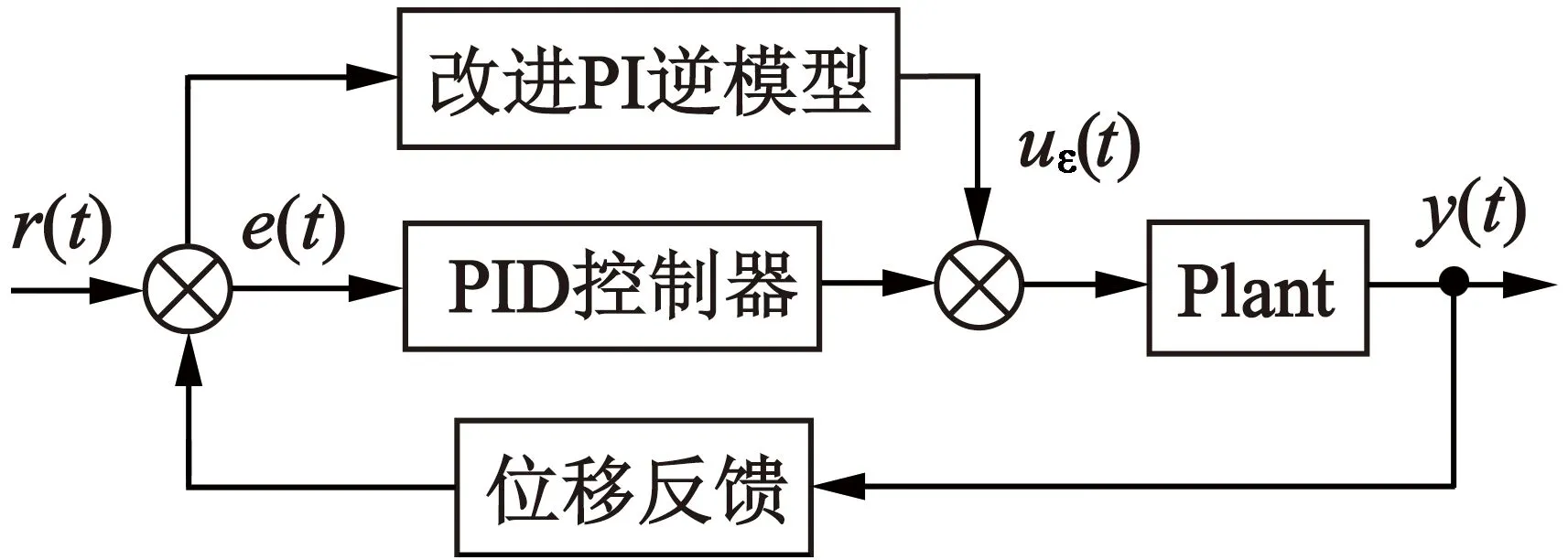
图4 前馈PID复合控制原理

2 压电驱动平台自适应闭环控制算法

2.1 基于单神经元的自适应PID控制

单神经元自适应PID控制算法：

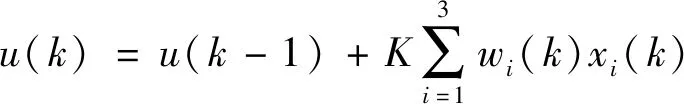
(5)

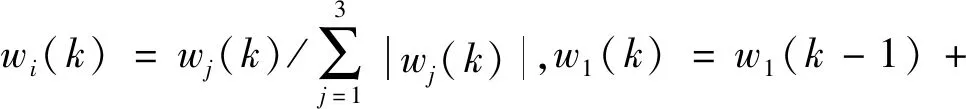
经过大量实践证明，可将单神经元自适应PID控制算法中的加权系数学习的修正部分进行修改,控制原理如图5所示。ηI，ηp和ηD为积分I、比例P、微分D的学习速率，K为神经元的学习速率[13]。

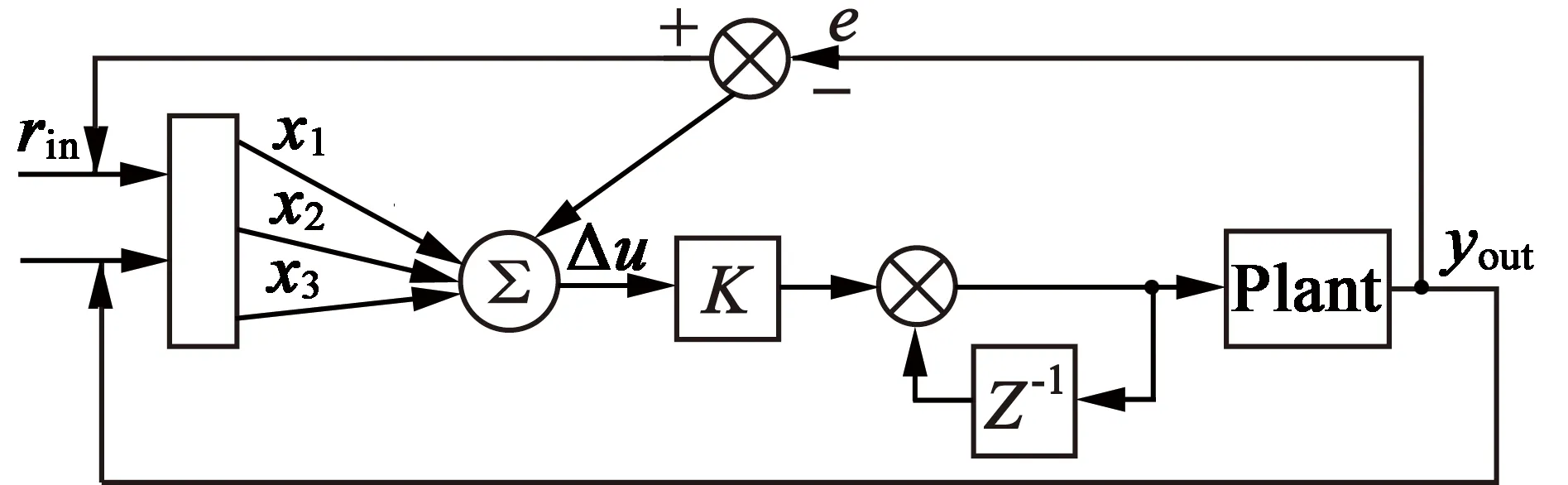
图5 单神经元自适应控制

改进的单神经元自适应PID系数在线修正主要是通过参考实际经验得出的，其仿真曲线如图6所示。

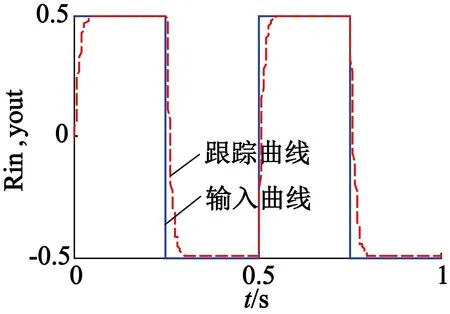
(a) 输入、跟随曲线

(b) 输入、跟随误差曲线

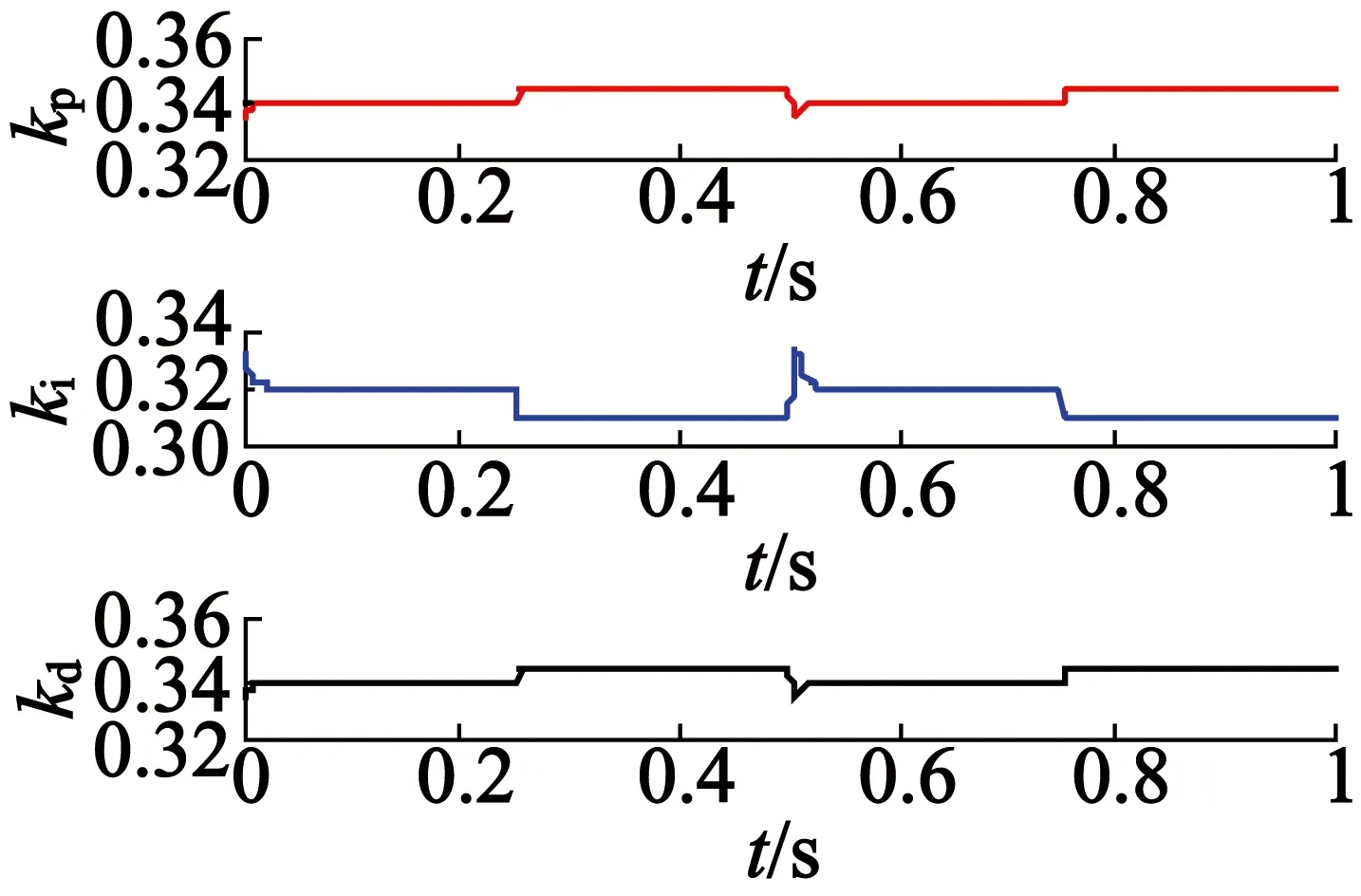
(c) PID参数变化曲线

2.2 基于BP神经网络的PID自适应控制

如图7所示，BP网络采用三层结构。网络输入层的输入:

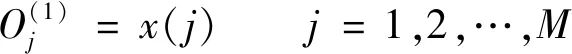
(6)

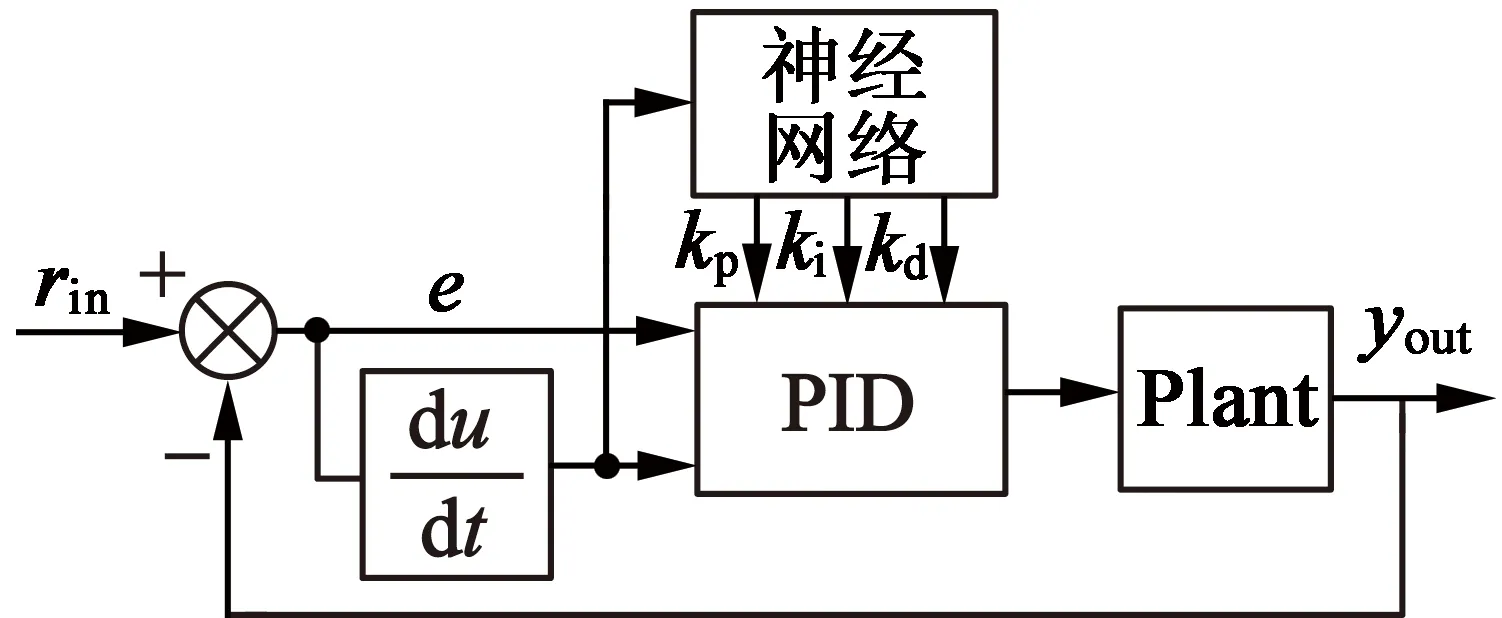
图7 基于BP神经网络整定的PID控制

在式(6)中,被控系统复杂程度决定输入变量数M。网络隐含层的输入、输出如下：

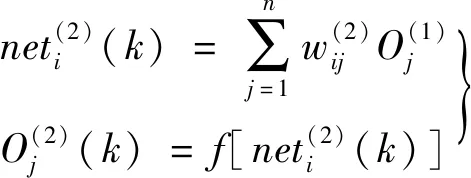
(7)

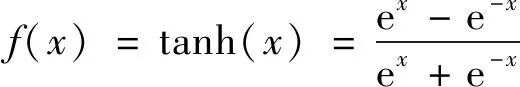
(8)

输出层的输入和输出如下:

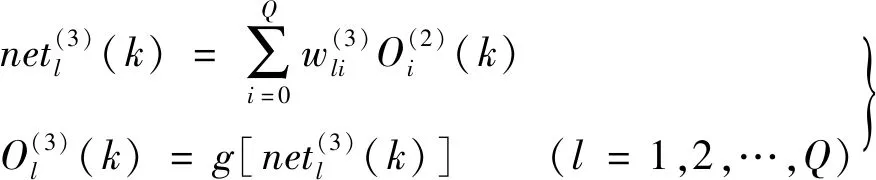
(9)

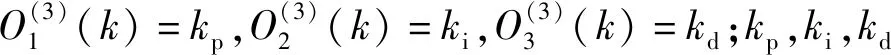
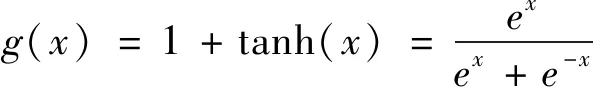
(10)

取性能指标函数如下式:

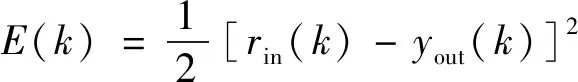
(11)

取性能指标函数E(k)的负梯度方向来修正网络的权系数，再加上能够使整个搜索更快速的惯性项，如下式:

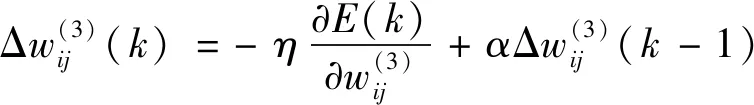
(12)

在式(12)中,η，α分别为学习率和惯性系数。输出层权的学习算法如下：

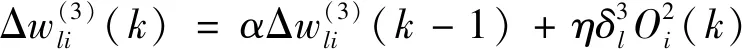
(13)

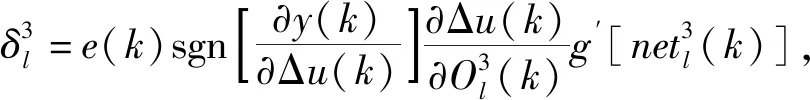
同理，可得隐含层加权系数的学习算法如下：

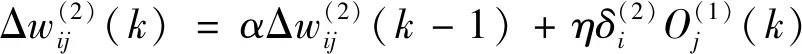
(14)

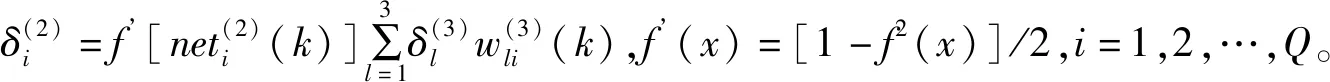
基于BP神经网络的PID控制算法仿真曲线如图8所示。从图8(a)和图8(b)中可以看出，跟随曲线与输入曲线的误差很小,验证了该算法的有效性；从图8(c)中可以看出，kp,ki,kd的值在实时调整,以调节跟随误差。

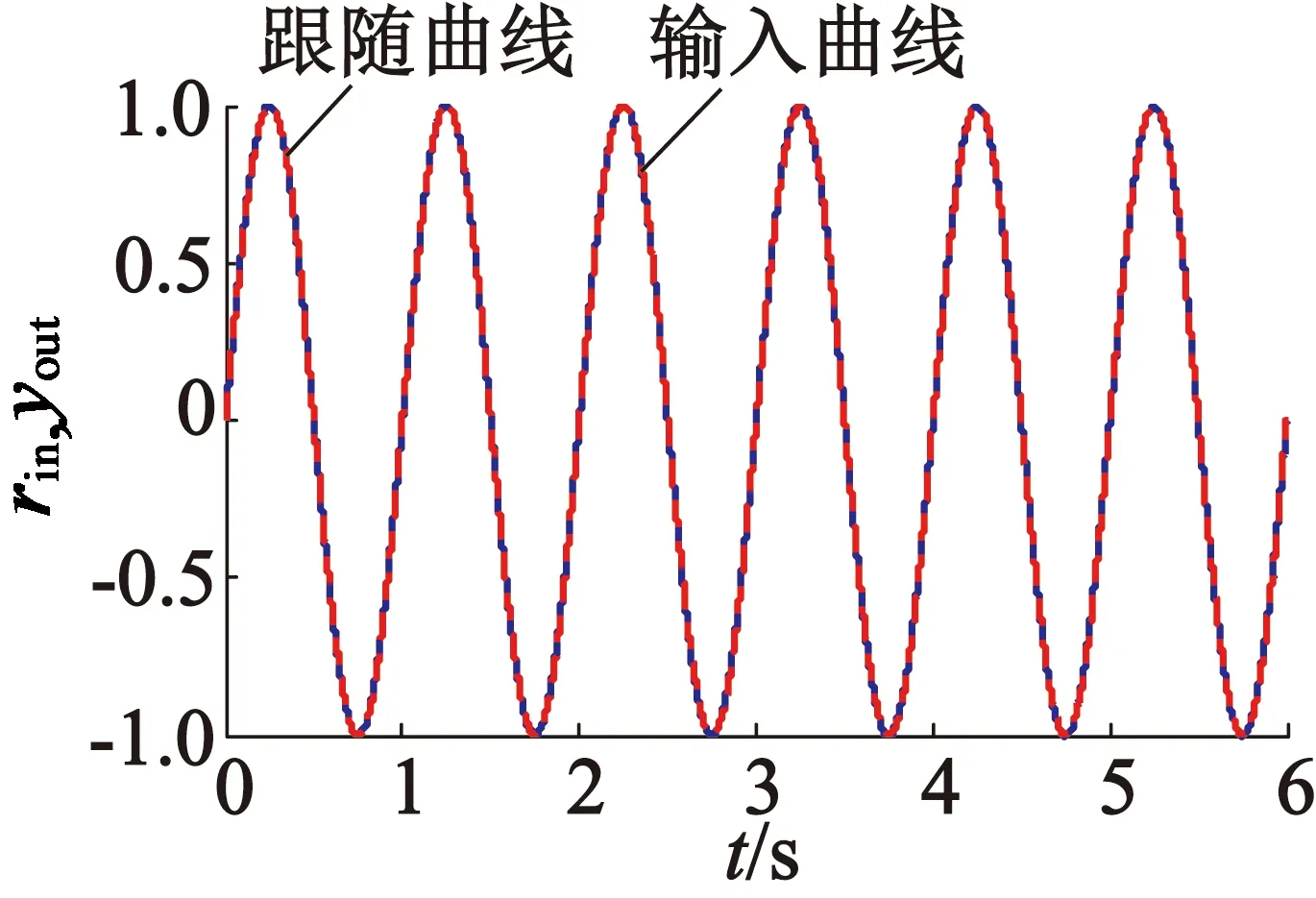
(a) 输入、跟随曲线

3 实验测试

根据实验需求，搭建了如图9所示的压电陶瓷驱动系统。

图9 压电驱动平台系统

STM32F407作为整个系统的主控芯片,利用D/A模块将电压通过高压运算放大电路输送到压电陶瓷,然后通过电阻片将压电陶瓷的位移反馈到传感器测量电路，经过处理后将电压传给A/D模块,电容传感器作为外部测量设备检测压电陶瓷运动平台的位移。

3.1 前馈PID控制实验

对压电驱动平台的驱动传动系统进行运动分析,得到其驱动传动系统的传递函数,由遗传算法全局寻优得到压电驱动平台的最优PID参数,在STM32F407中实现前馈PID控制算法,其实验效果如图10所示。由图10(a)可知,在电压上升和下降

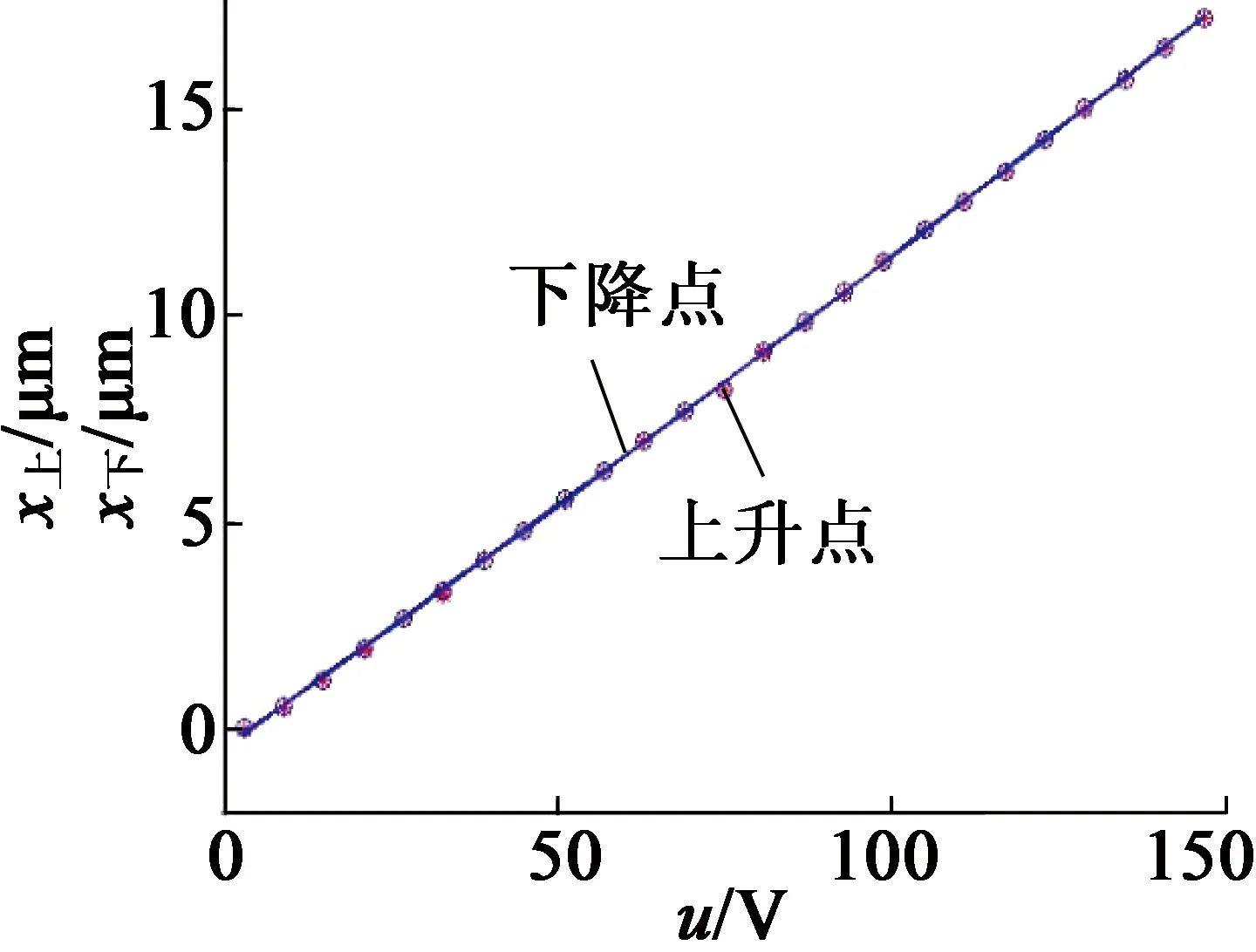
(a) 前馈PID控制效果

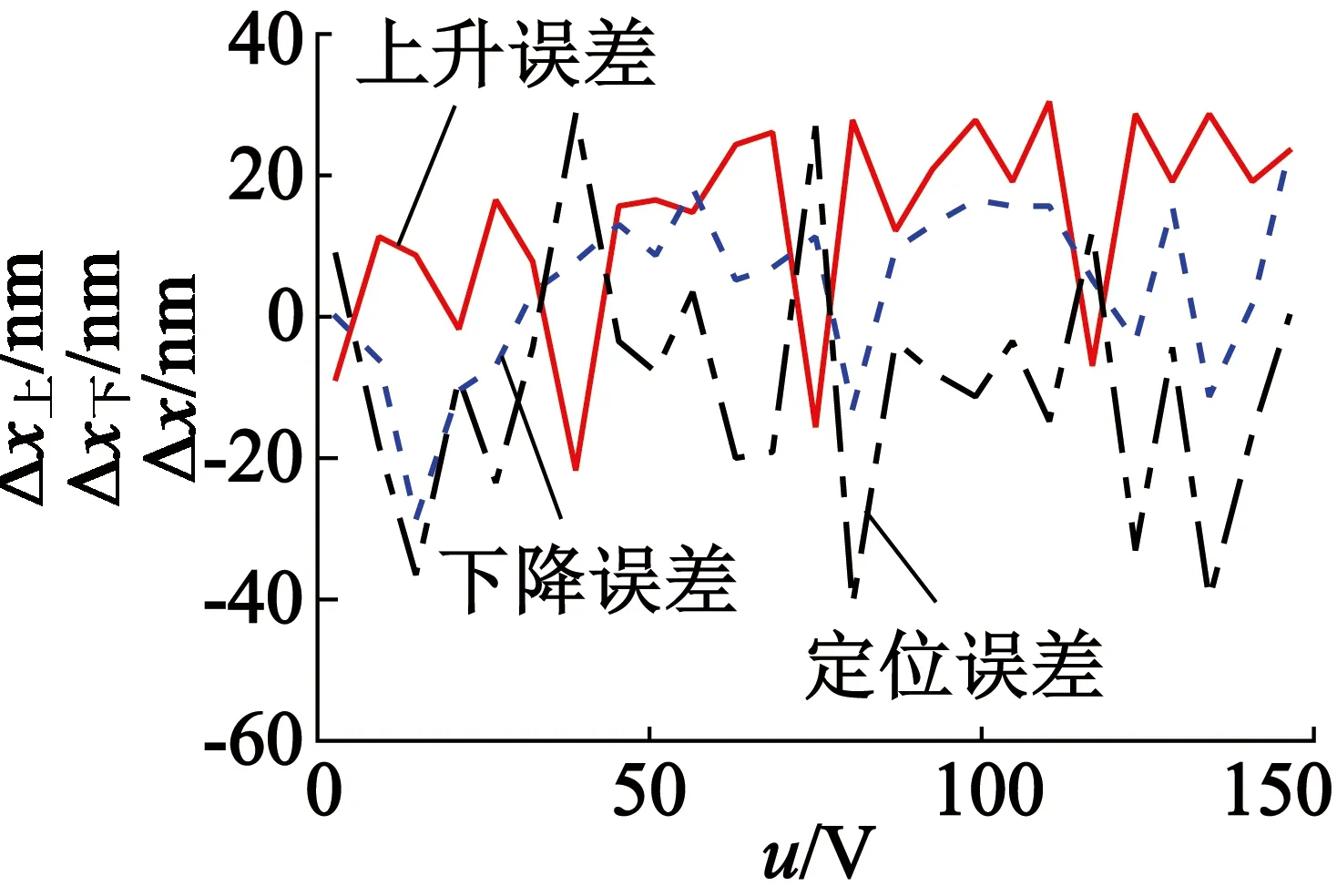
(b) 前馈PID控制定位误差

时，平台的定位精度得到提高。前馈PID控制算法定位误差曲线如图10(b)所示,其最大定位误差为40.5 nm,最小定位误差为3.0 nm,平均定位误差为16.5 nm。

3.2 改进的单神经元自适应PID控制实验

基于单神经元自适应PID控制,其权系数的在线修正主要是通过参考实际经验来确定的。单神经元自适应PID控制算法的实验效果如图11所示。从图11中可以看出，单神经元自适应PID控制算法相比于前馈PID控制算法具有更好的线性度。单神经元自适应PID算法定位误差曲线如图11(b)所示,其最大定位误差为18.5 nm,最小定位误差为0.5 nm,平均定位误差8.3 nm。

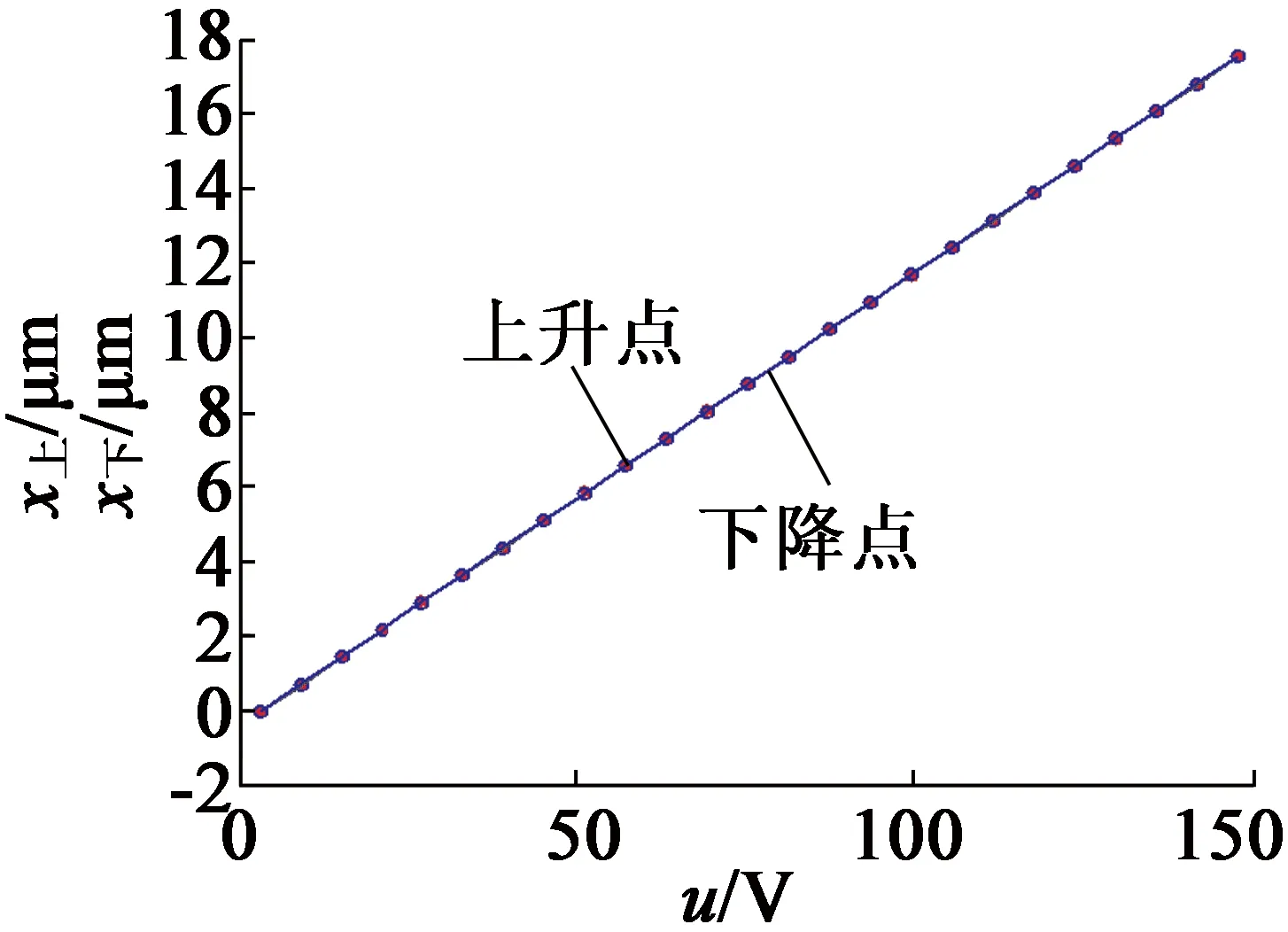
(a) 单神经元自适应PID控制效果

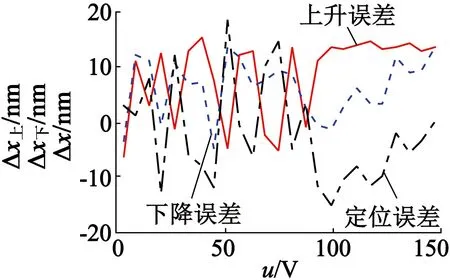
(b) 单神经元自适PID算法定位误差

3.3 基于BP神经网络PID控制实验

在BP网络PID控制中, 3个参数kp，ki，kd的在线调整主要是通过神经元的自学习来实现的。该控制算法也是在STM32F407中来实现,实验效果如图12所示。基于BP神经网络PID控制算法相比单神经元自适应PID算法具有更好线性度。其定位误差曲线如图12(b)所示,最大定位误差为14.0 nm,最小定位误差为0.5 nm,平均定位误差5.1 nm。

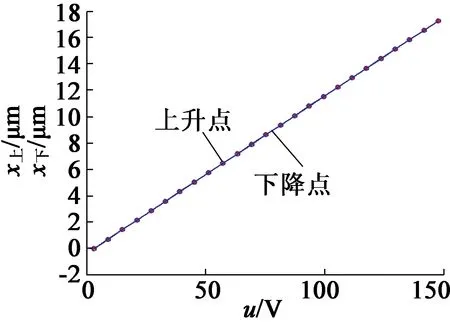
(a) BP神经网络整定PID算法控制效果

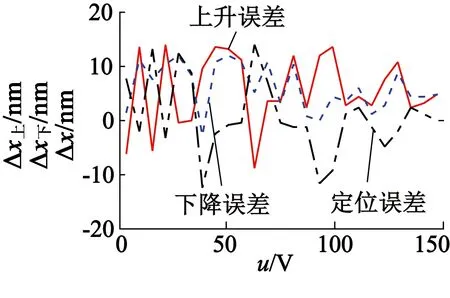
(b) BP神经网络整定PID算法定位误差

4 结 语

本文建立了压电驱动平台的驱传动系统的等效动力学模型,为遗传算法提供目标函数。形成了以非对称PI迟滞模型为前馈模型的前馈PID复合控制；运用基于改进的单神经元自适应PID控制和基于BP神经网络的PID控制，实现PID参数的在线实时闭环控制。

搭建了压电陶瓷驱动平台实验系统,进行闭环控制实验。实验结果显示，驱动平台在前馈PID控制下平均定位误差为16.5 nm;在单神经元自适应PID算法的控制下平均定位误差8.3 nm;基于BP神经网络自整定PID控制算法平均定位误差5.1 nm。自适应PID闭环控制精度优于前馈PID控制，神经网络PID控制精度高于单神经元自适应PID控制。