不同永磁形状的内置式永磁电机空载性能比较

倪有源，王 磊

(1.合肥工业大学，合肥 230009; 2. 安徽大学 高节能电机及控制技术国家地方联合工程实验室，合肥 230601)

0 引 言

相对于其他类型电机，永磁电机拥有效率高、体积小以及转矩密度高等优点[1]，永磁电机被广泛地应用在航空航天、国防、交通运输、工农业生产和公共生活等方面。目前，对永磁电机的研究主要是以表贴式永磁电机为主，这类电机具有调速快，运行稳定且结构简单等优点。但是在调速范围和高速运行下的稳定性等方面，表贴式永磁电机比内置式永磁电机差。内置式永磁电机的永磁嵌入在转子里，于是就没有表贴式永磁电机在高速运转时永磁会脱落的缺点，特别是内置式永磁同步电机在恒定功率的条件下具有调速范围宽、过载能力强和功率密度高等优势，广泛应用在新能源电动汽车中[2]。近年来，对内置式永磁电机的研究越来越广泛。内置式永磁电机转子结构复杂，且因永磁体和隔磁桥对电机性能的影响，对内置式永磁电机的电磁性能研究，较少采用解析法分析[3-4]，大多运用有限元法进行设计、分析以及优化[5-10]。

本文运用二维有限元法分析了长方体和瓦形两种不同形状的内置式永磁电机的空载性能。分析了永磁的结构变化对电机空载磁场参数的影响，然后分析在两种形状的永磁体用量不变的条件下，改变永磁体的位置和厚度，得到了永磁体位置和厚度对内置式永磁电机空载参数的影响规律。

1 内置式永磁电机结构

图1给出了长方体永磁和瓦形永磁两种永磁形

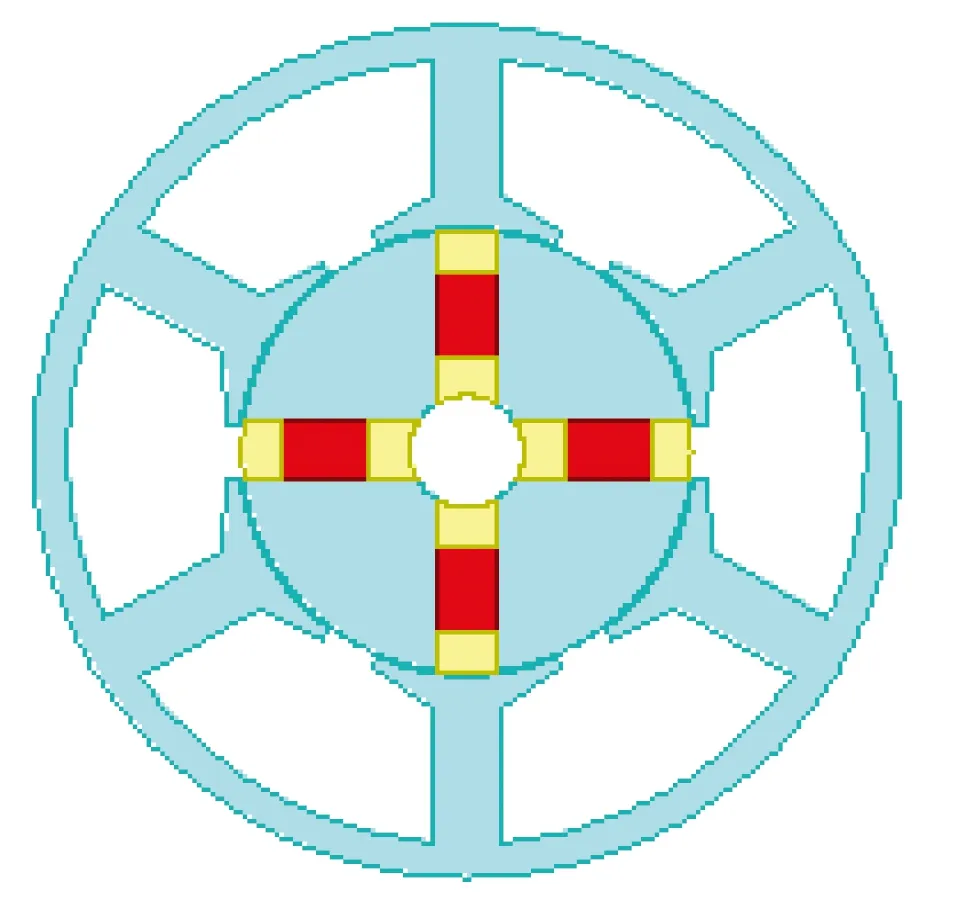
(a) 长方体永磁

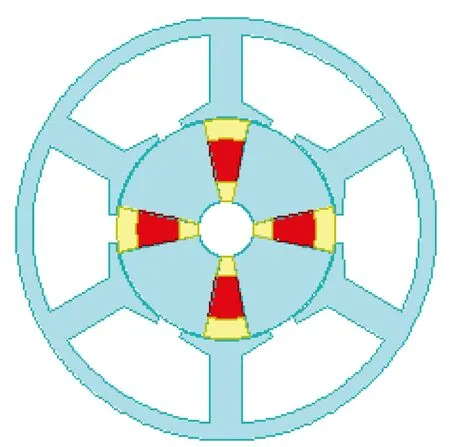
(b) 瓦形永磁

图1两种内置式永磁形状

状的内置式永磁电机结构。这两种电机的定子结构参数完全相同，但转子磁路不相同，于是得到的电机性能也不同。

一台3相、6槽4极内置式永磁电机的主要参数如表1所示。该电机的额定转速3 000 r/min，定子和转子铁心采用的是50W470的硅钢片，0.5 mm叠压。永磁牌号是钕铁硼N33。

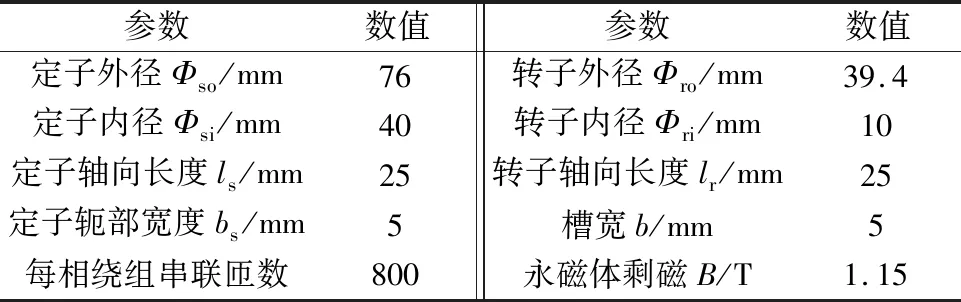
表1 内置式永磁电机的主要参数

2 两种磁极形状的空载磁场比较

运用二维有限元法，得到长方体永磁和瓦形永磁的两种电机空载磁力线分布如图2所示。

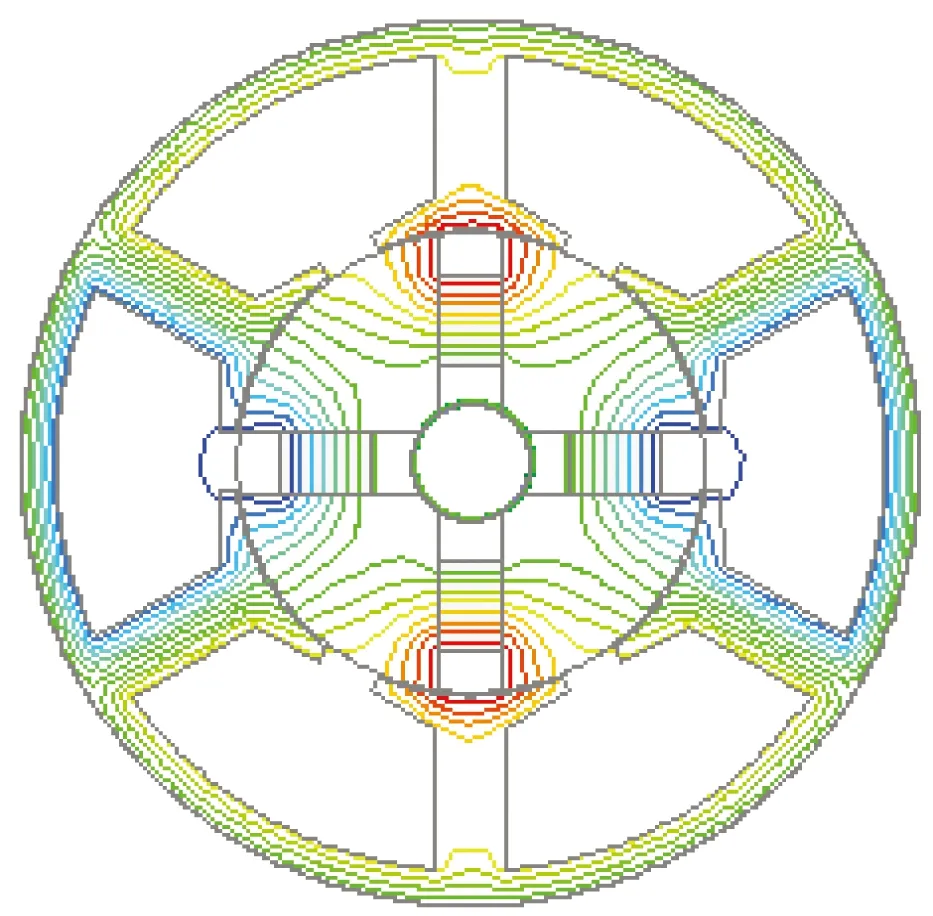
(a) 长方体永磁

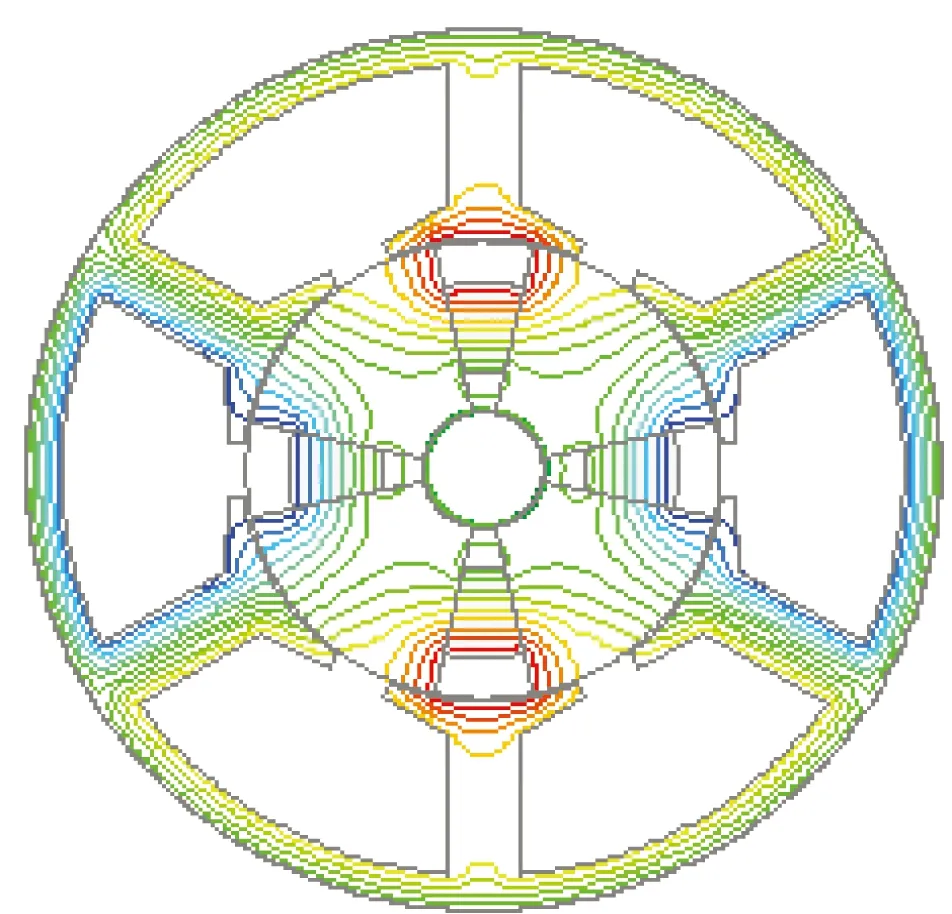
(b) 瓦形永磁

图2两种永磁形状的空载磁力线分布

运用二维有限元法，计算两种不同形状永磁的空载磁场参数。图3(a)和图3(b)分别为长方体永磁和瓦形永磁的气隙径向磁密波形。对这两个波形进行傅里叶分解，得到气隙径向磁密的基波和谐波，如图4所示。两种磁极形状的气隙径向磁密基波幅值和THD值如表2所示。

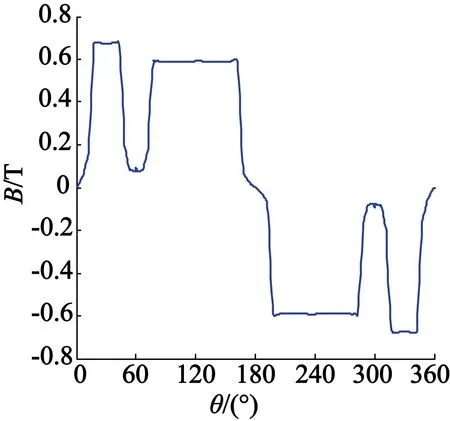
(a) 长方体永磁

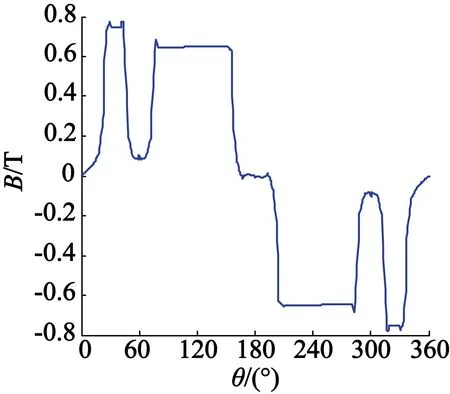
(b) 瓦形永磁

图3两种永磁形状的气隙径向磁密波形

图4 两种永磁形状的气隙径向磁密基波和谐波

从这些图表可知，长方体永磁比瓦形永磁的气隙径向磁密的基波值小，且瓦形永磁的THD值小于长方体永磁的THD值。就气隙磁密而言，瓦形永磁优于长方体永磁。

表2 两种永磁形状的气隙径向磁密

图5(a)和图5(b)分别为长方体永磁和瓦形永磁的内置式永磁电机的空载感应电动势波形。分别对两个空载感应电动势进行傅里叶分解，得两种永磁形状的感应电动势基波和谐波，如图6所示。两种永磁形状的感应电动势的基波和THD值如表3所示。

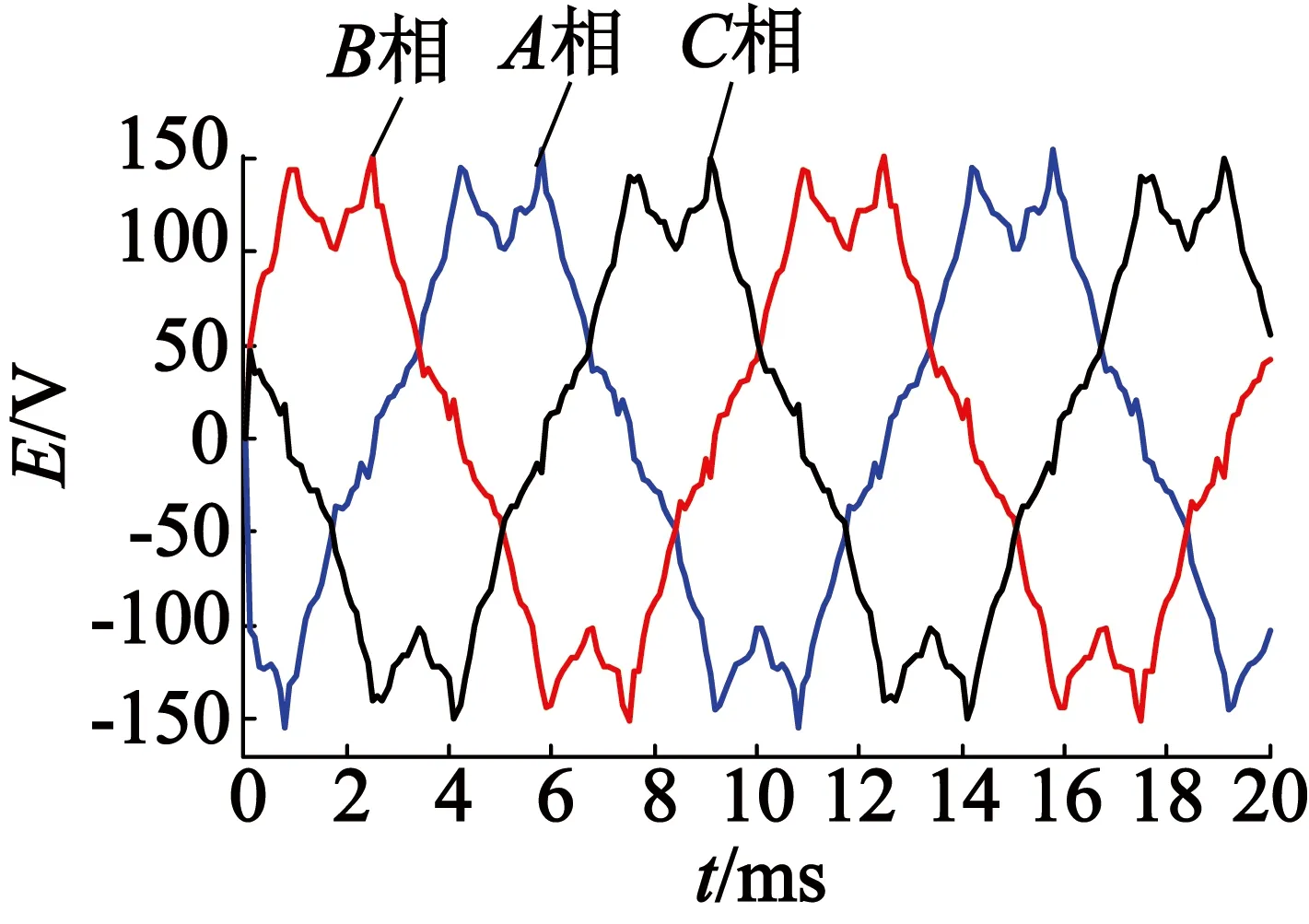
(a) 长方体永磁

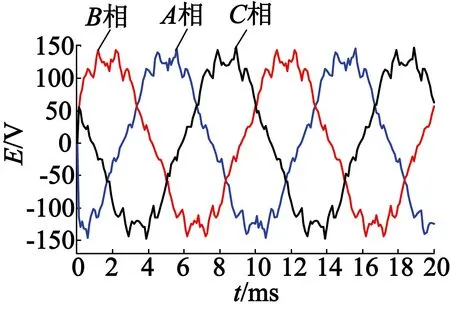
(b) 瓦形永磁

图5两种永磁形状的感应电动势波形

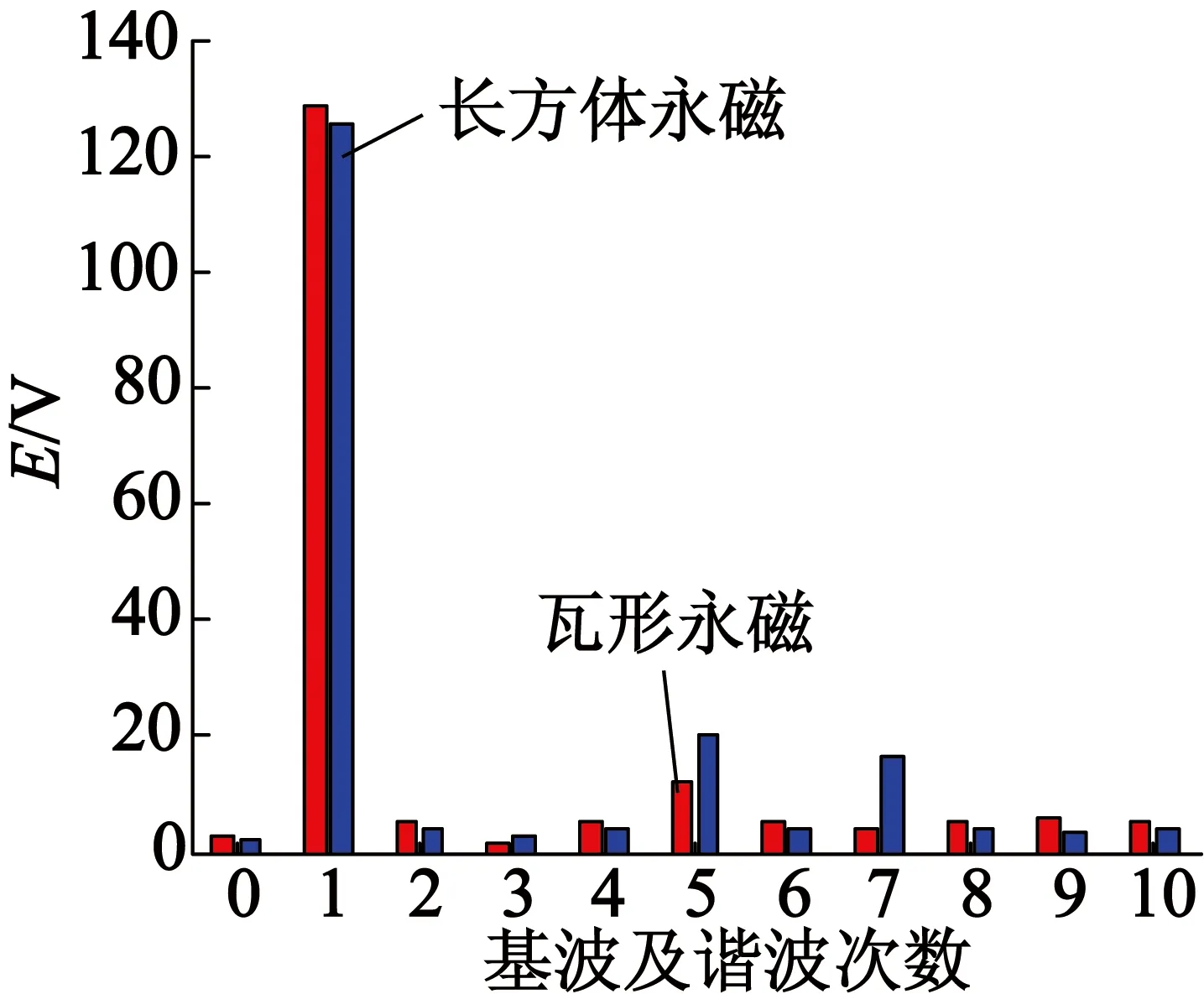
图6 两种永磁形状的感应电动势基波和谐波

永磁形状感应电动势基波幅值E/V感应电动势THD/%长方体125.626.55瓦形128.423.00

可以看出，长方体永磁比瓦形永磁的感应电动势的基波值小，且瓦形永磁的THD比长方体永磁的THD值小。从感应电动势这方面来看，瓦形永磁优于长方体永磁。

图7(a)和7(b)分别为两种永磁形状的内置式永磁电机的齿槽转矩波形。从图7中可看出，长方体永磁的齿槽转矩的峰值为48.17 mN·m，瓦形永磁的齿槽转矩峰值为152.28 mN·m。显然，长方体永磁优于瓦形永磁。

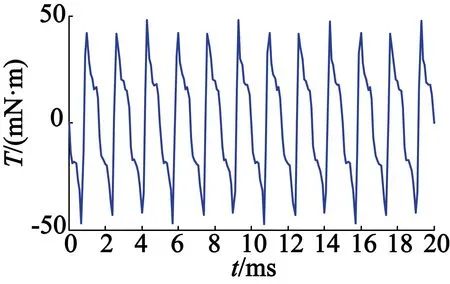
(a) 长方体永磁

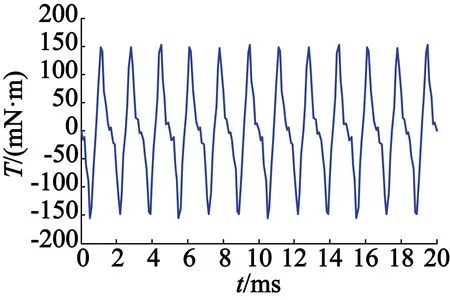
(b) 瓦形永磁

图7两种永磁形状的齿槽转矩波形

3 永磁位置对空载磁场的影响

3.1 长方体永磁

长方体永磁的结构如图8所示。h1和h2分别为永磁的下表面和上表面离转轴中心的距离。保持永磁大小和形状不变，通过改变永磁的位置，分析永磁的不同位置对电机空载磁场的影响。这里，h1首先从5 mm开始，即永磁下表面在转子的内径处，然后h1每次增加1.4 mm，增加到12 mm时，即永磁上表面在转子的外径处，运用有限元法得到永磁不同的位置对电机空载磁场的影响。

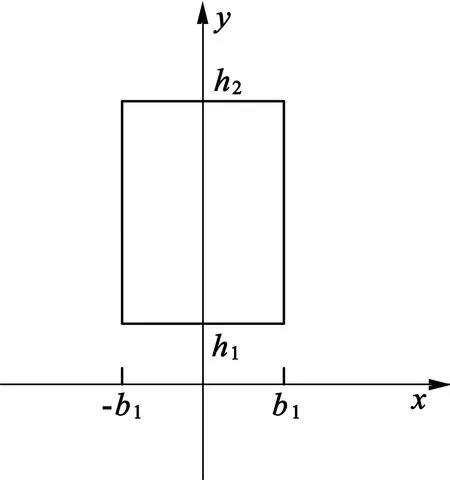
图8 长方体永磁截面

随着h1的变化，即永磁的位置发生变化时，气隙径向磁密的基波幅值和THD值的变化情况如表4所示。从表4中可以看出，当h1变化时，气隙磁密的基波幅值和THD的值变化不明显。随着h1的变化，空载感应电动势基波幅值和THD值的变化情况如图9所示。从图9中可以看出，随着h1的变化，空载感应电动势的基波幅值和THD值变化不大。随着h1的变化，齿槽转矩变化波形图如图10所示。

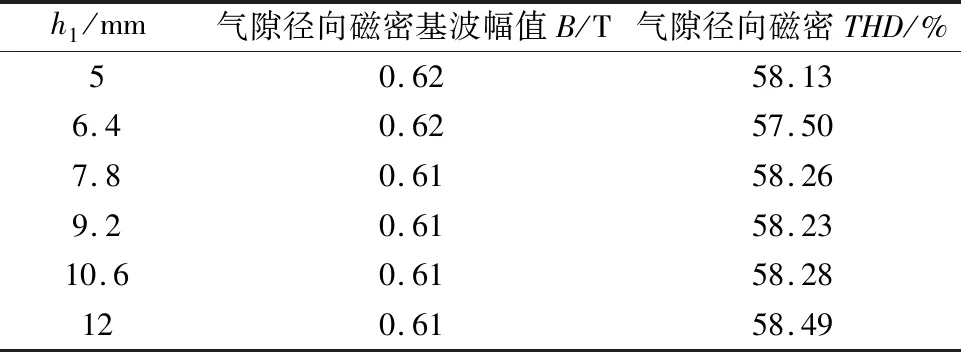
表4 长方体永磁在不同位置的气隙径向磁密

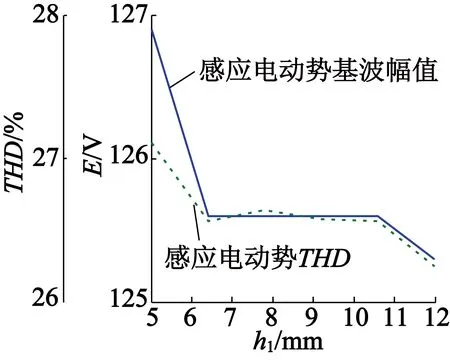
图9 长方体永磁位置对

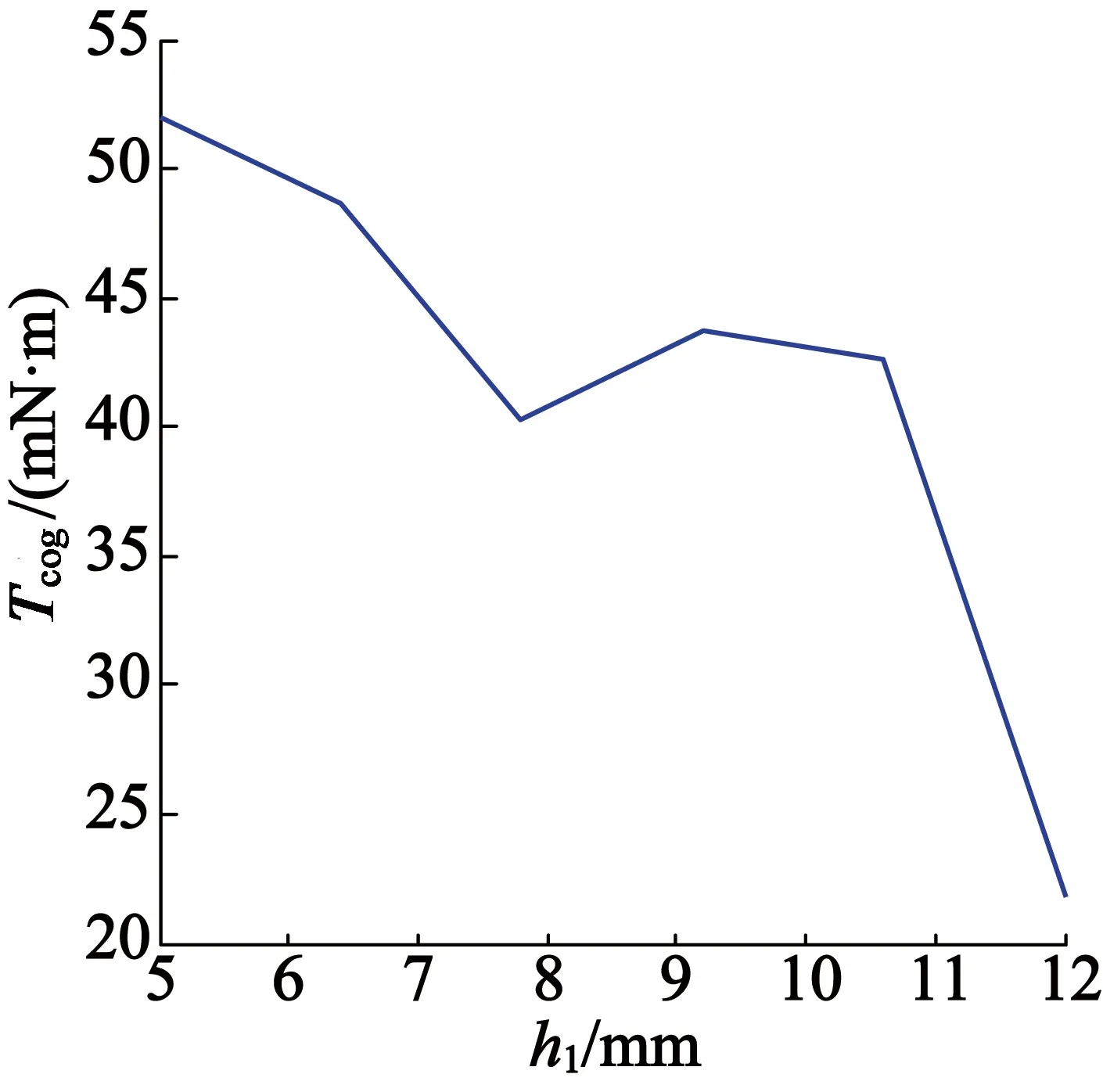
图10 长方体永磁位置对

从这些图表可知，永磁的位置变化对内置永磁电机的空载性能影响较小。永磁的位置接近转子内表面处，气隙磁密和感应电动势优于永磁接近转子的外表面处。而永磁在中间处和转子外径处的齿槽转矩优于永磁在其它位置。

3.2 瓦形永磁

瓦形永磁的结构如图11所示。保持永磁大小和形状不变，由于需要提供铁心磁路，所以转子铁心形状需要稍微改变。也分析瓦形永磁的不同位置对电机空载磁场的影响。当永磁的位置变化时，h1的变化与长方体永磁位置变化情况一样。

图11 瓦形永磁截面

运用有限元方法，得到瓦形永磁h1不同值时的气隙径向磁密。然后计算相应的气隙径向磁密基波幅值及其THD，如表5所示。可以看出，随着h1的增加，瓦形永磁的内置式永磁电机气隙径向磁密基波幅值逐渐减小，THD值先增大再减小然后增大。

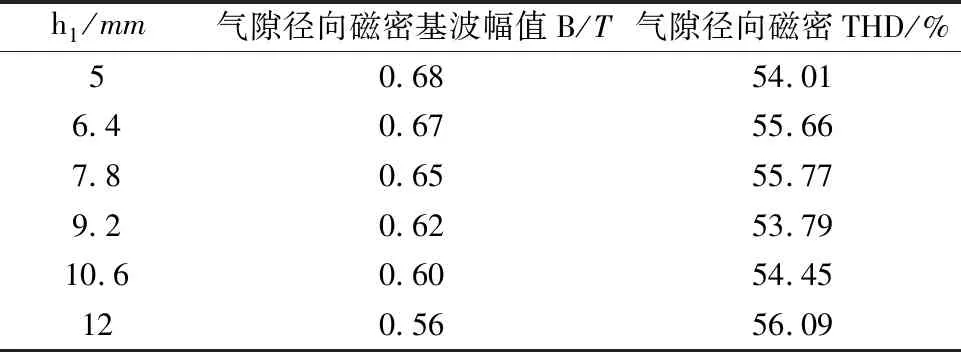
表5 瓦形永磁不同位置的气隙径向磁密

随着h1值的变化，瓦形永磁内置式永磁电机的感应电动势的基波幅值和THD值的变化情况如图12所示。从图12中可以看出，随着h1的增加，感应电动势的基波值减小，THD值先减小再增大然后减小。随着h1的变化，齿槽转矩的变化情况如图13所示。从图13中可以看出，随着h1的增加，齿槽转矩的峰值先减小后增大再减小。

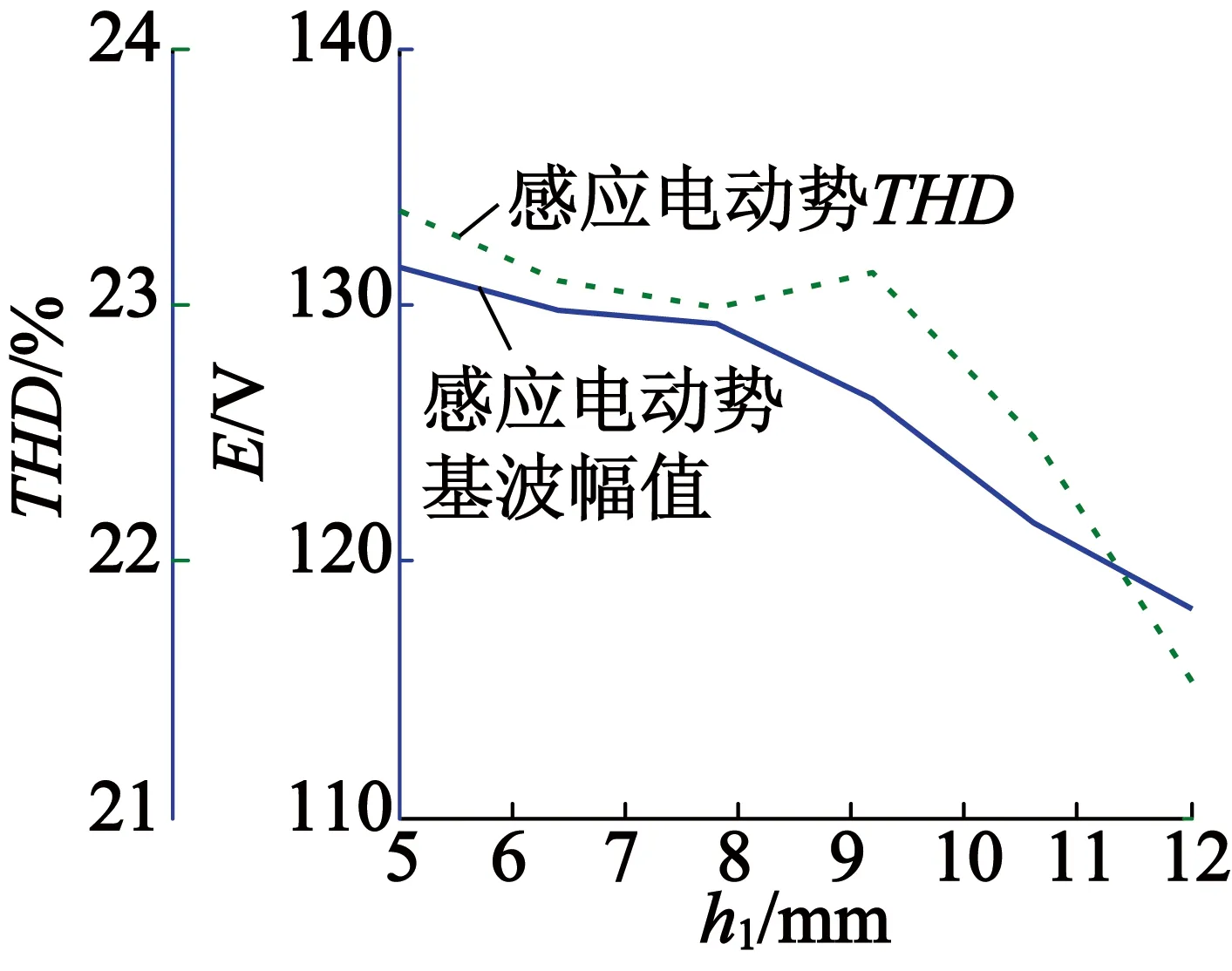
图12 瓦形永磁不同位置对

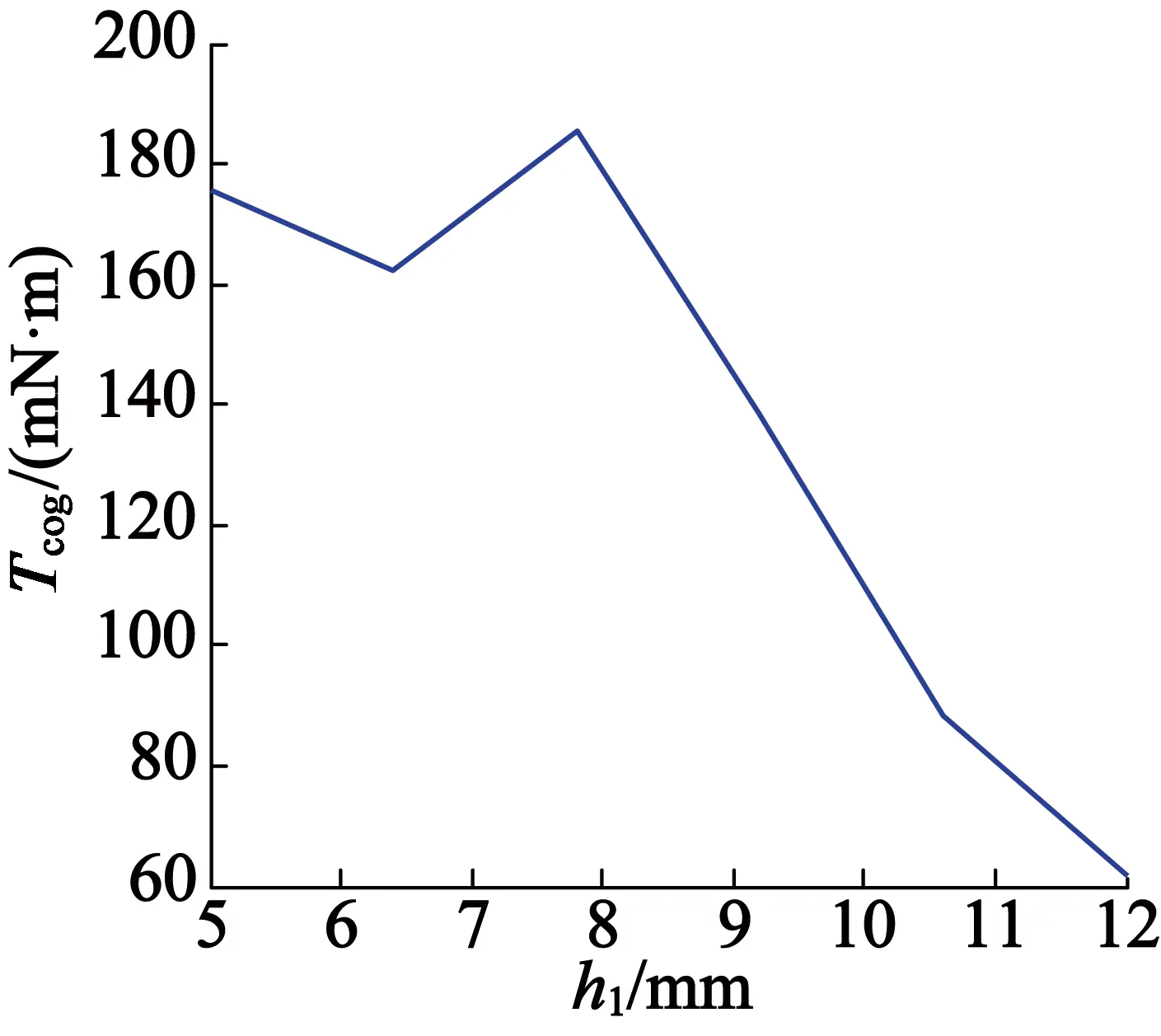
图13 瓦形永磁不同位置对

4 永磁厚度对空载磁场的影响

4.1 长方体永磁

图8中，长方体永磁的截面为矩形，h2-h1为永磁厚度。保持永磁的形状和体积不变，即截面积不变，逐次增加永磁厚度，使b1值减小，这里取中心为初始值，步长为上下各增加0.7 mm。

在永磁量不变的情况下，运用有限元法得到长方体永磁在不同厚度的气隙径向磁密波形。计算得到不同永磁厚度下气隙径向磁密基波幅值及THD，如表6所示。可以看出，随着永磁厚度增加，长方体永磁的内置式永磁电机气隙径向磁密基波幅值和THD值都增大。

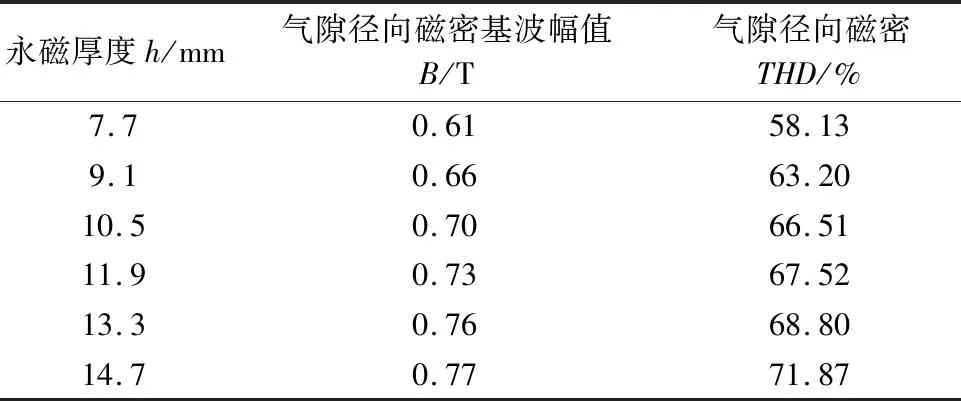
表6 长方体永磁不同厚度下的气隙径向磁密

随着永磁厚度变化，感应电动势基波幅值和THD值的变化情况如图14所示。从图14中可以看出，随着永磁厚度的增加，感应电动势的基波幅值先增大后减小，而THD值一直增大。永磁厚度变化时，齿槽转矩变化如图15所示。可以看出，随着永磁厚度的增加，齿槽转矩峰值先增大然后减小。

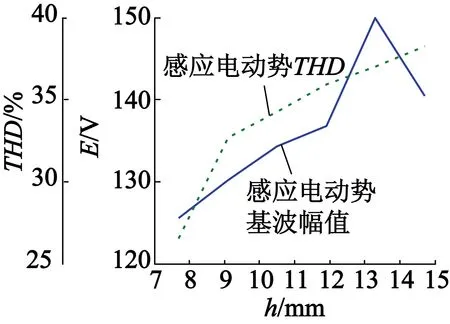
图14 长方体永磁厚度对

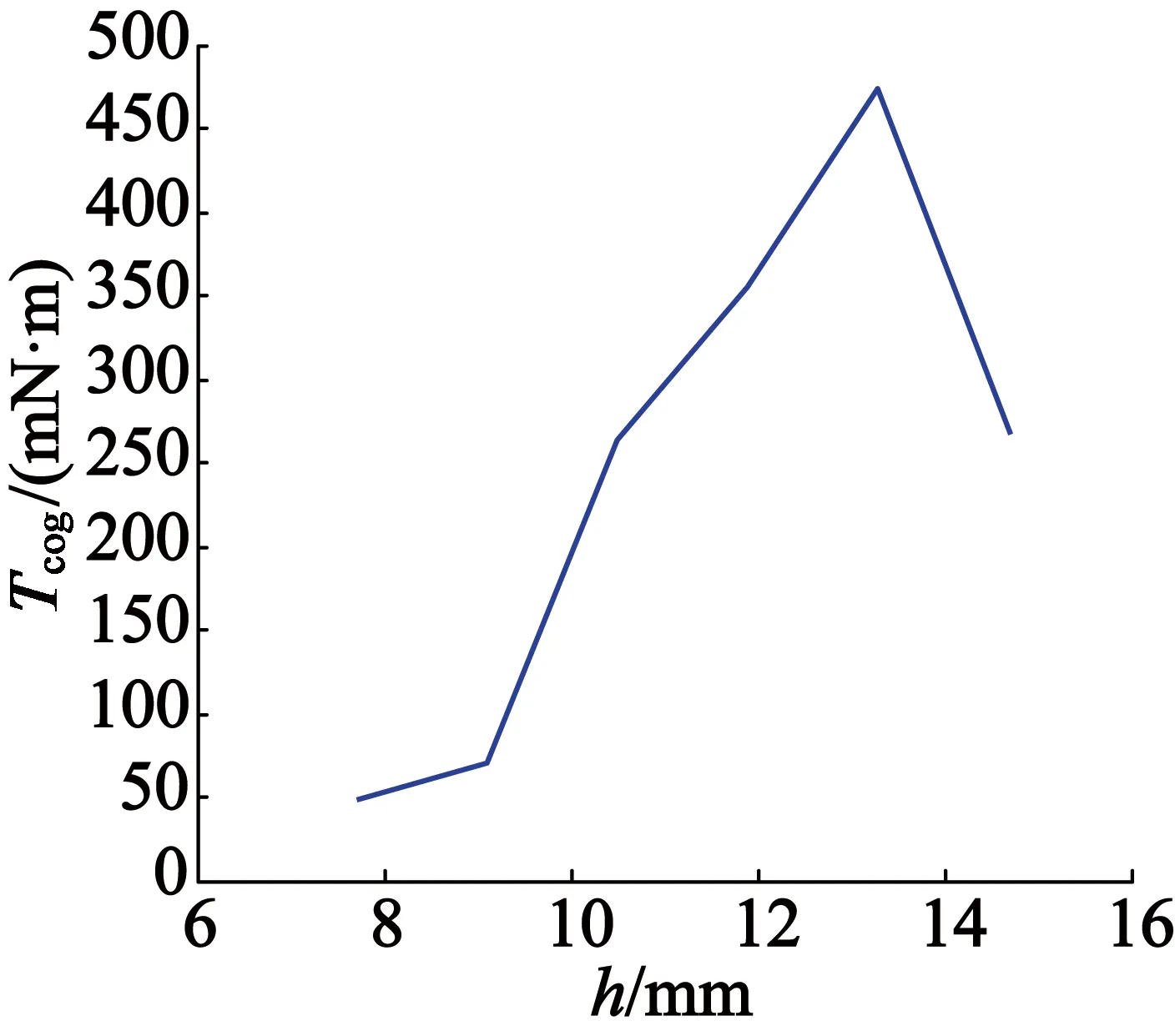
图15 长方体永磁厚度对

4.2 瓦形永磁

在永磁形状和体积不变的情况下，依次改变永磁厚度，运用有限元法得到瓦形永磁不同厚度下的气隙径向磁密。再计算相应的气隙径向磁密基波幅值及THD，如表7所示。可以看出，随着永磁厚度的增加，瓦形永磁的内置式永磁电机气隙径向磁密基波幅值和THD值都增大。

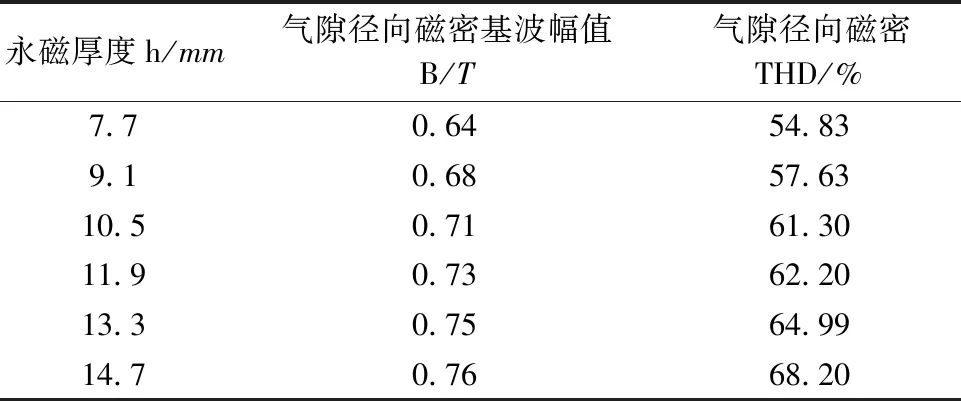
表7 瓦形永磁不同厚度下的气隙径向磁密

随着永磁厚度的增加，瓦形永磁电机感应电动势的基波幅值和THD的变化情况如图16所示。从图16中可以看出，随着永磁厚度的增加，感应电动势的基波和THD都增大。

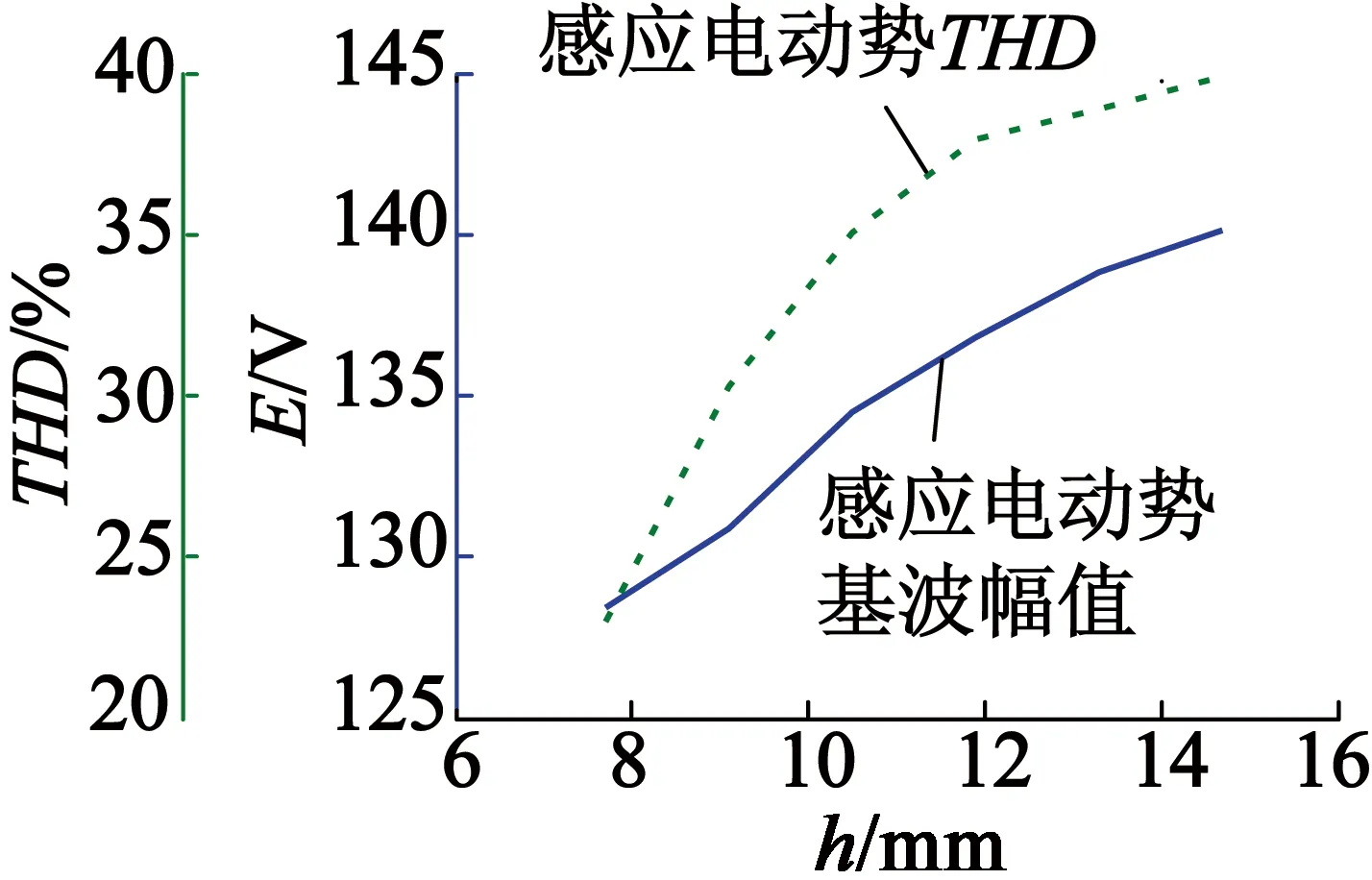
图16 瓦形永磁厚度对感应电动势的影响

随着瓦形永磁厚度的增加，齿槽转矩的变化情况如图17所示。从图17中可以看出，随着永磁厚度的增加，齿槽转矩的峰值先增加后减小再增加。

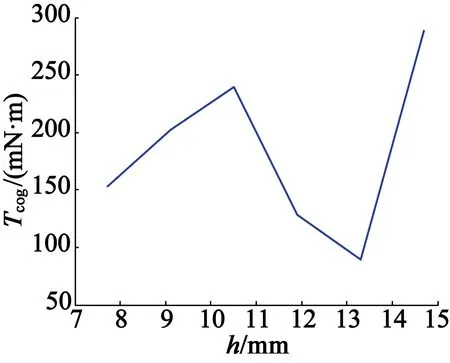
图17 瓦形永磁厚度对齿槽转矩峰值的影响

5 结 语

有限元法计算结果很精确，适用于分析复杂结构的电机性能。本文运用二维有限元方法，分析了长方体永磁和瓦形永磁两种不同形状的内置式永磁电机的空载电磁性能。计算结果表明，瓦形永磁的气隙磁密和感应电动势优于长方体永磁，但齿槽转矩高于长方体永磁。分析了两种永磁在不同位置处的电机空载电磁性能，保持永磁大小和形状不变的前提下，改变长方体永磁位置对内置式永磁电机空载磁场影响很小。而对于瓦形永磁，虽然永磁形状不变，但是转子铁心形状发生改变，于是在不同位置时，电机空载电磁性能发生了改变。最后，保持永磁量不变，随着永磁厚度的增加，瓦形永磁的气隙径向磁密和感应电动势的基波幅值和THD都增加，长方体永磁的气隙径向磁密的基波幅值和THD也增加，而感应电动势的基波幅值先增大后减小，THD随之增大。本文为内置式永磁电机的结构性能优化提供了理论参考。