五相混合式步进电动机不同主电路电流纹波分析

肖申平,王晓琳,鲍旭聪

(南京航空航天大学,南京 211106)

0 引 言

混合式步进电动机综合了反应式和永磁式步进电动机输出力矩大、动态性能好、步距角小的优点，已经成为市场上应用最多的步进电动机种类，适用于低速定位场合，在工业生产中得到了广泛应用。按照定子绕组来分，混合式步进电动机有两相、三相、四相和五相等系列，其中两相混合式步进电动机占据市场主导地位，但多相电机技术的发展也正逐渐改变混合式步进电动机领域的格局。随着电力电子技术的发展，电机的相数不再受供电相数的约束，多相电机凭借其独特的优势正逐渐成为研究的热点。文献[1-2]提出使用多相电机和对应的驱动器技术来应对电力机车、电动汽车、多电飞机、舰船电力推进、风力发电和航空航天等场合对驱动器中低压大功率和高可靠性的要求。文献[3-4]对多相逆变器的PWM方法进行了深入研究, 提出了具有提高电压利用率、消除共模电压等性能的脉宽调制方法。文献[5]利用开绕组式的逆变器对多相电机的容错控制进行了有效的探索。综上，多相电机在低压大功率、高可靠性、低转矩脉动场合有着得天独厚的优势[6-10]。而在步进电动机领域，五相混合式步进电动机具有初始步距角小、转矩大等特点，在精度要求较高的低速大功率定位场合，有着不可替代的应用前景。

五相混合式步进电动机驱动系统的运行品质与驱动器的性能紧密相关，众多学者关注高性能五相混合式步进电动机驱动器的研究与设计。混合式步进电动机要求定子绕组双极性供电[6]，常用的拓扑结构有H桥结构和五相半桥两种。五相混合式步进电动机绕组采用开路的形式，H桥拓扑结构下绕组的连接方式唯一确定；而在五相半桥结构下根据绕组不同的连接方式又可以分为星形连接和五边形连接。因此，混合式步进电动机有3种常用的主电路：H桥主电路、五相半桥星形主电路以及五相半桥五边形主电路。

H桥主电路在五相混合式步进电动机驱动系统中的应用与研究较少。由于功率器件数量过多，在五相混合式步进电动机系统中很少采用H桥结构的主电路。但在两相混合式步进电动机驱动系统中，H桥主电路是最为常用的主电路，有着良好的动态性能表现[11-12]。另外，有学者在五相永磁同步电机领域使用H桥主电路实现电机的容错运行。本文对这种主电路在五相混合式步进电动机驱动系统中的性能表现进行了研究；另外，五相混合式步进电动机定子绕组的互感因素很少被考虑。五相半桥星形主电路和五相半桥五边形主电路是目前最常用的两种主电路，文献[13-15]对于它们可行性、驱动能力的分析已经有较为完整的叙述，但是都没有考虑互感的影响。本文在数学模型中加入互感，从电流纹波的角度重新考量这3种主电路的性能。

本文从五相混合式步进电动机的数学模型理论分析推导了各种主电路下的电流纹波表达式。在整步运行的基础上解算出电流变化率绝对值的最大值，以此为指标预测不同拓扑下电流纹波的大小，分析不同拓扑控制策略下电流纹波的极限所在，旨在选取五相混合式步进电动机驱动系统高精度要求下的最优主电路。通过仿真和实验验证了理论的正确性。

1 系统数学模型

1.1 五相混合式步进电动机数学模型

五相混合式步进电动机等效电路图如图1所示。图1中，ea，eb，ec，ed，ee分别为发电机定子相反电动势；ia，ib，ic，id，ie分别为发电机定子相电流；Ra，Rb，Rc，Rd，Re为发电机定子相电阻。五相混合式步进电动机定子采用开绕组的结构[4]，ua+，ub+，uc+，ud+，ue+分别代表A，B，C，D，E五相绕组的正端，ua-，ub-，uc-，ud-，ue-分别代表负端。

图1 五相混合式步进电动机等效电路图

由于五相混合式步进电动机多工作于电动机状态，所以本文以电动机的标注惯例对数学模型中的各个参数进行标注，其中相电流的参考方向与相电压的参考方向一致，与反电动势的参考方向相反，每相绕组的电压方程：

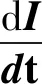
(1)

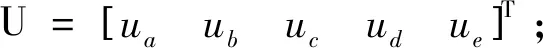
从电压方程可以看出，每相绕组上的压降主要由4部分组成，分别是电阻上的压降、反电动势、自感上的感应电动势和其他相的互感产生的感应电动势。

电机电感与绕组电流和转子位置角有关，其中绕组电流的大小影响磁场饱和的程度，本文不考虑饱和带来的影响。文献[16]通过实验得出结论，五相混合式步进电动机的电感随转角位置的变化主要是二次谐波，且波动量不超过±5%，因此，可以忽略转子位置角对电感的影响。

文献[16]指出电感矩阵具有以下特点：

1)每相绕组的自感相等；

2)互感参数只有两种，相邻相的互感相同，相隔相的互感相同，都约为自感的1/4。

因此，五相混合式步进电动机的电感矩阵Ls表达式如下：

式中：L0为各相绕组的自感。

为了让理论推导更接近实际情况，对电感矩阵做适当修正，取实际五相混合式步进电动机的电感值作为本文推导的依据，修正后的电感矩阵如下：

1.2 五相导通整步运行模式

五相混合式步进电动机初始步距角较小，整步运行模式下就能达到较好的平稳性。另外，每相绕组单独作用，分别正负通电时会产生10个方向的转矩[17-18]，如图2所示。

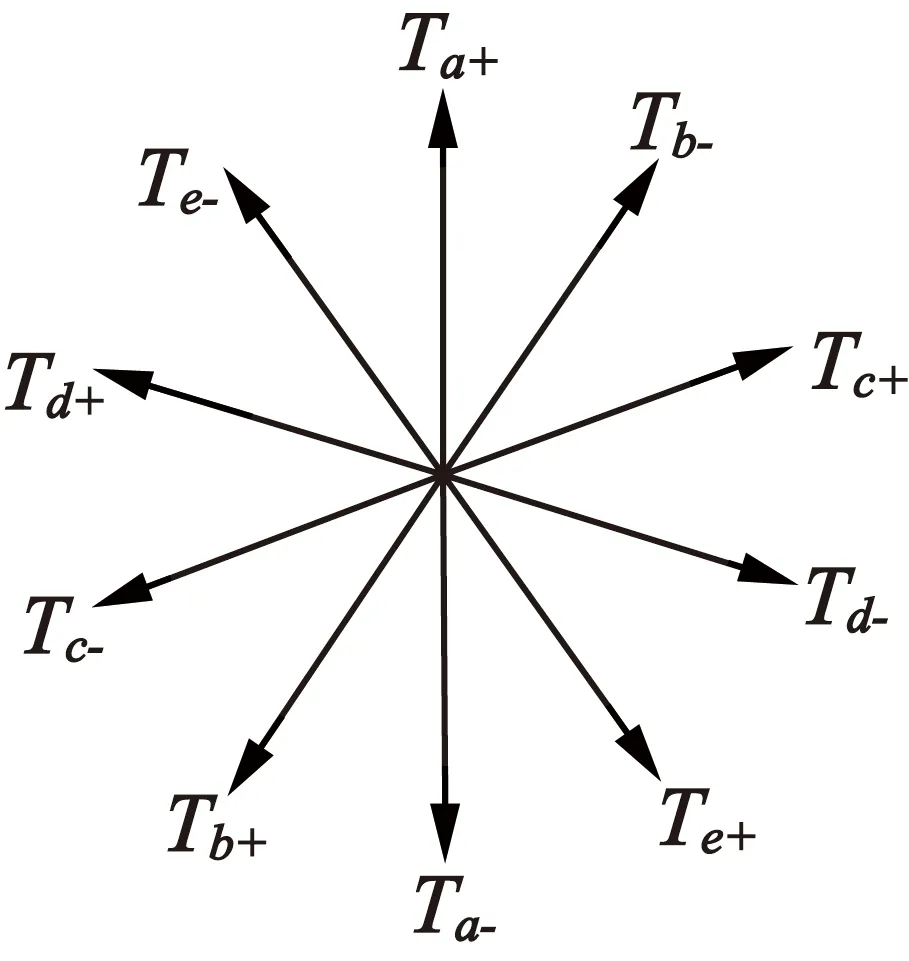
图2 五相绕组转矩矢量图

为了尽可能发挥五相混合式步进电动机高转矩的特性，应增加导通相数，每次导通5相时有最大转矩，此时的运行模式即为五相十拍驱动方式[19-21]。具体时序与导通状态如表1所示。本文在这种电机驱动模式下分析电流纹波的大小。

表1 五相励磁时序表

2 电流纹波分析

2.1 H桥结构电流纹波分析

H桥结构是步进电动机经典的拓扑结构，由于电机定子采用开绕组的形式，因此将绕组的两端分别接至H桥的两个桥臂中点就能方便地实现双极性驱动，五相混合式步进电动机采用H桥结构的电路拓扑如图3所示[22-23]。

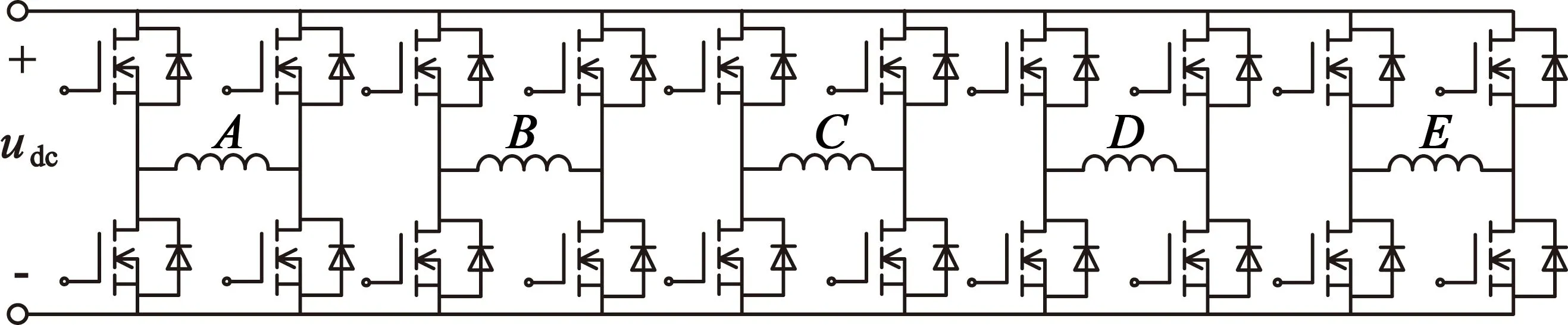
图3 H桥结构电路拓扑图

采用这种连接方式，每相绕组之间没有物理上的连接，每相单独控制，只会受到其他相互感的影响，其等效电路图与图1一致。为方便求解，忽略绕组电阻上的压降，列写此时的电压方程组如下：

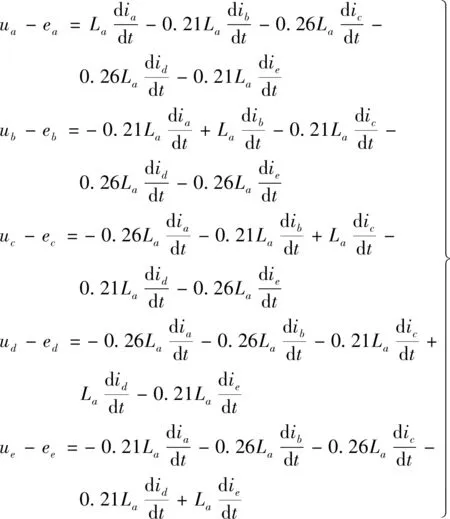
(2)

若在稳态下，每相的端电压和反电动势可以看作常量，以每相的电流变化率为变量，此方程组是一个五元一次方程组，并且方程个数为5，有且只有一个唯一解。五相绕组具有对称性，因此只分析A相绕组的电流变化率，解方程组得到：

3.19(ua-ec)+3.19(ua-ed)+

3.15(ua-ee)]

(3)

由式(3)可以看出，A相绕组电流变化率取决于该时刻的五相绕组端电压，而电流纹波的大小取决于电流变化率绝对值的最大值。

H桥连接下每相绕组的端电压由开关组合决定:当前时刻电流实际值小于给定时，给绕组施加正电压udc；当前时刻电流实际值大于给定时，绕组施加负电压-udc[18]。五相绕组互相独立控制，因此式(3)绝对值的最大值是在每相绕组端电压都取正电压udc时。五相混合式步进电动机运行在低速情况下，反电动势的大小相比于母线电压很小，为了简化结果，取ea=eb=ec=ed=ee=e0,udc-e0=u0,那么在H桥连接下电流变化率绝对值的最大值：

2.2 星形连接电流纹波分析

星形连接下的电路拓扑图如图4所示。

图4 星形连接电路拓扑图

星形连接下的五相绕组电压方程如下：

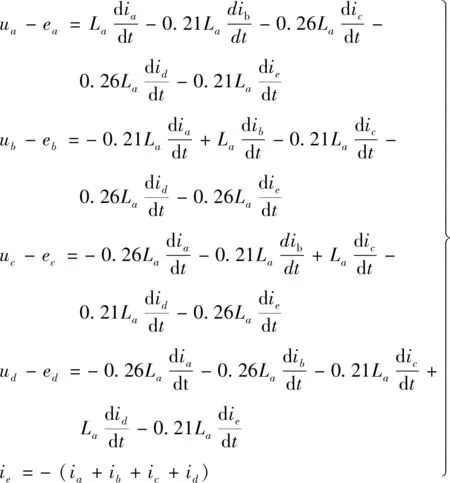
(4)

星形连接方式下绕组间有了物理上的连接，正向导通的绕组需要通过反向导通的绕组才能形成回路，五相绕组之间的电流满足五相电流和为0这一约束条件[3]。

解式(4)方程组得到A相绕组电流变化率的表达式：

0.032 8(uc-ec)+0.032 8(ud-ed)]

(5)

同理，要预测星形连接下的电流纹波大小就得求出A相绕组电流变化率绝对值的最大值。与H桥结构不同，星形连接下各绕组的端电压的取值不仅与自身电流情况有关，还与其他相电流取值有关。

星形连接下的电流控制策略：当电流实际值小于给定时，就开通该相的上桥臂，让该相正向导通；当电流实际值大于给定时，就开通该相的下桥臂，让该相反向导通[19-20]。实际运行时五相电流都是在各自的给定电流附近上下跳动的锯齿波，某一时刻的每一相桥臂开关状态与其他相相互独立，因此五个桥臂的开关管组合共有32种。按照正向导通绕组个数，这32种状态大致可以分为5大类：正向导通相数分别为0，1，2，3，4。

在二胡教学的过程中，教师应当对学生进行积极正确的引导和帮助，帮助学生搭建起高效的学习框架，逐渐从感性教学过渡到理性教学，最终实现实践教学，通过不断的循环实践锻炼，提高学生的二胡演奏技能。

如果每个桥臂的上管开通用1表示，下管开通用0表示，5个开关管的组合可以用一个5位的二进制数表示，例如10100表示A，C上管开通，B，D，E下管开通。这32种开关组合状态具体导通状态如表2所示。

表2 开关组合表

不同的开关组合对应的端电压也不相同，电流纹波取决于各个时段电流超过给定值的最大值，因此,在32种组合中找到使得式(5)取到绝对值最大值的组合，就能确定在整个运行过程中产生电流纹波的大小。

将表(2)中的值一一代入，就能求得状态10000和状态01111下的端电压能够使得A相电流变化率表达式得到绝对值的最大值:

2.3 五边形连接电流纹波分析

当五相混合式步进电动机采用五边形连接时，电路使用了10个开关管来驱动电机的运行。电路拓扑图如图5所示。

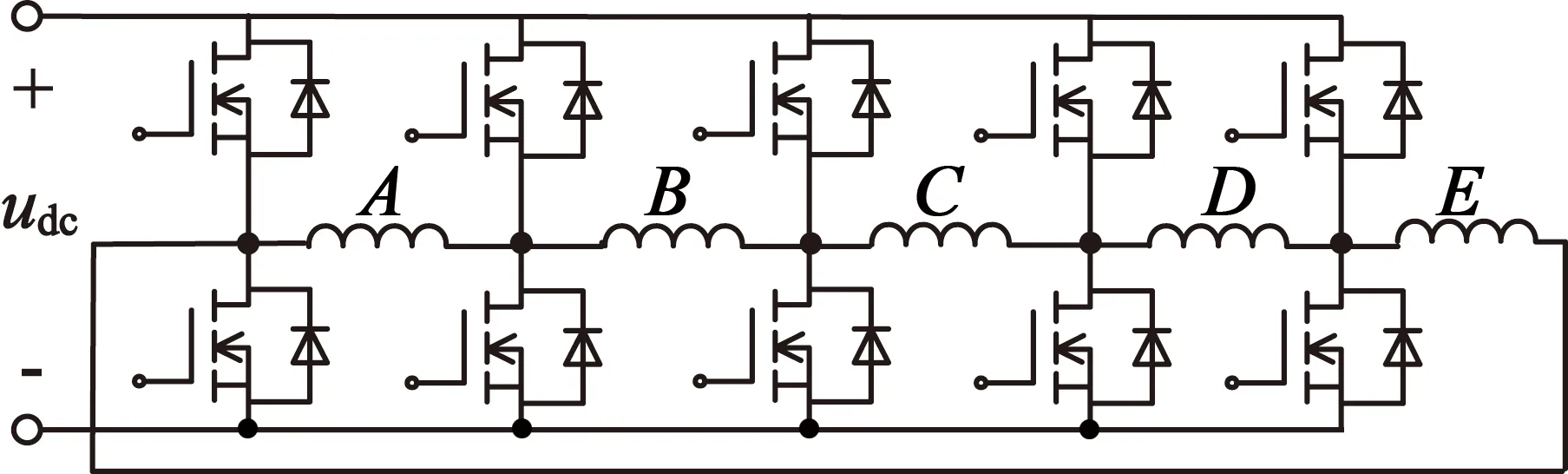
图5 五边形电路拓扑结构

这种连接方式具有以下特点：五相绕组五边形连接，流向相同的绕组电流相等；电流采用恒总流控制，只需要一个电流传感器，成本较低。

五边形与星形连接不同点在于采集反馈电流进行控制。当母线电流小于给定电流，查表输出开关状态；当母线电流大于给定电流，所有开关管关断[9]。另外，五边形连接中，电流流向相同的电流相等，例如在表1时序1中存在A，C，E相绕组电流相等，B，D相绕组电流相等，五相绕组的电压方程可以写成：

(6)

解式(6)方程组得：

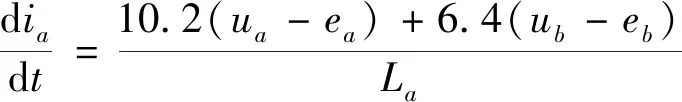
(7)

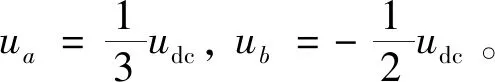
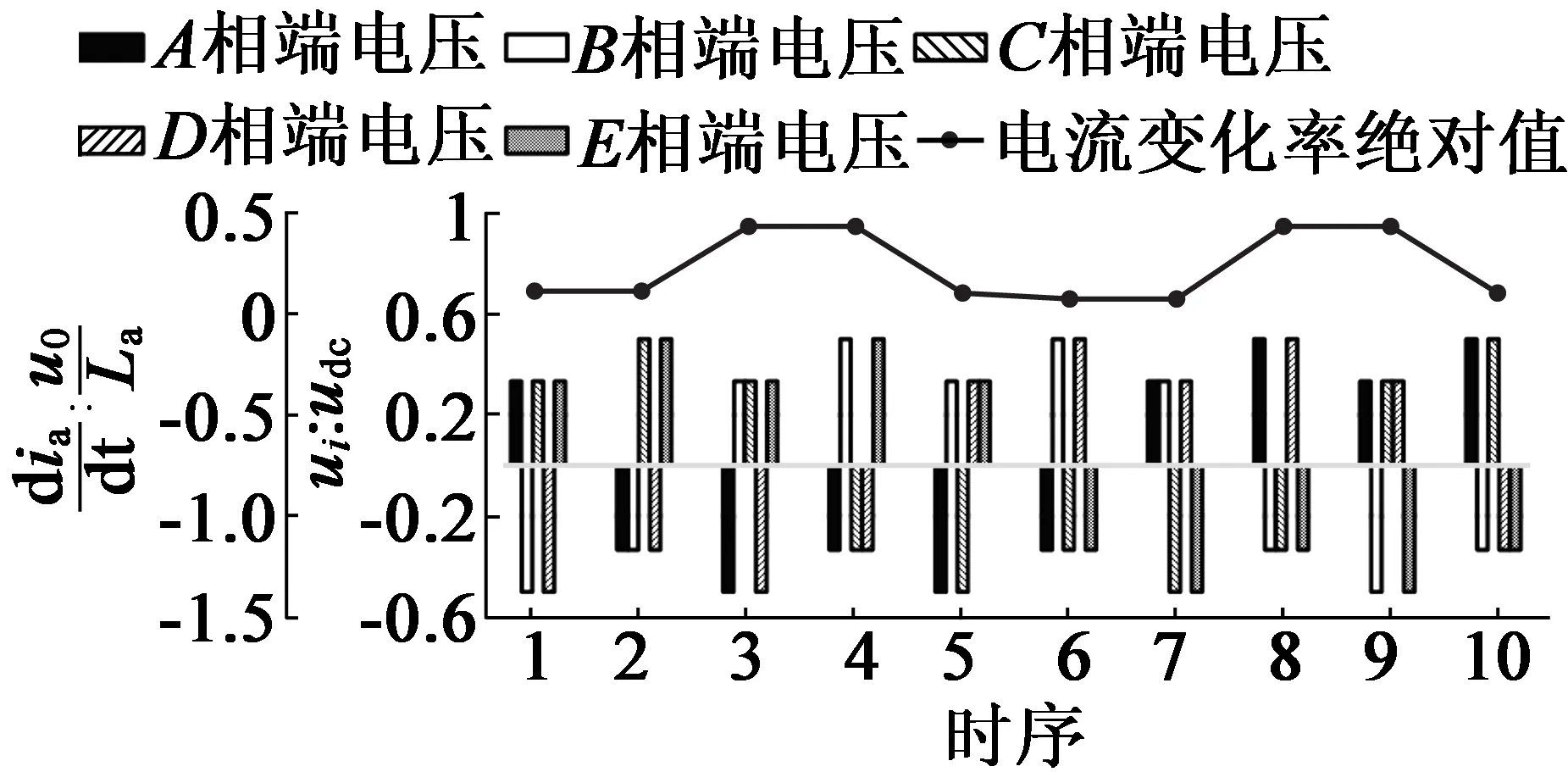
图6 各相端电压与电流变化率绝对值示意图

在一个周期内，A相绕组的电流变化率绝对值最大值：

以上分析了3种主电路下的绕组电流约束关系，列写了五相绕组的电压方程，从而解算出A相绕组在一个周期内的电流变化率绝对值的最大值，以此为指标分析电流纹波的大小。

3种拓扑下电流变化率绝对值的最大值有着明显的差异，H桥结构下的电流变化率绝对值远远大于后两种拓扑，相比于单相导通时的电流变化率，增大了近10倍，由此可以推断在控制周期不变的情况下，使用H桥结构驱动五相混合式步进电动机会产生较大的电流纹波，电机可能无法正常运行。而采用五相半桥拓扑会有较好的效果。

3 仿真分析与实验验证

3.1 仿真分析

本文的仿真条件以及电机参数如表3所示。

表3 仿真参数表

在上述仿真条件和电机参数下进行了3种拓扑的仿真验证，将具体参数代入，根据上文推导，3种拓扑下，A相电流的变化率最大值可以计算得出，理论值如图7所示。

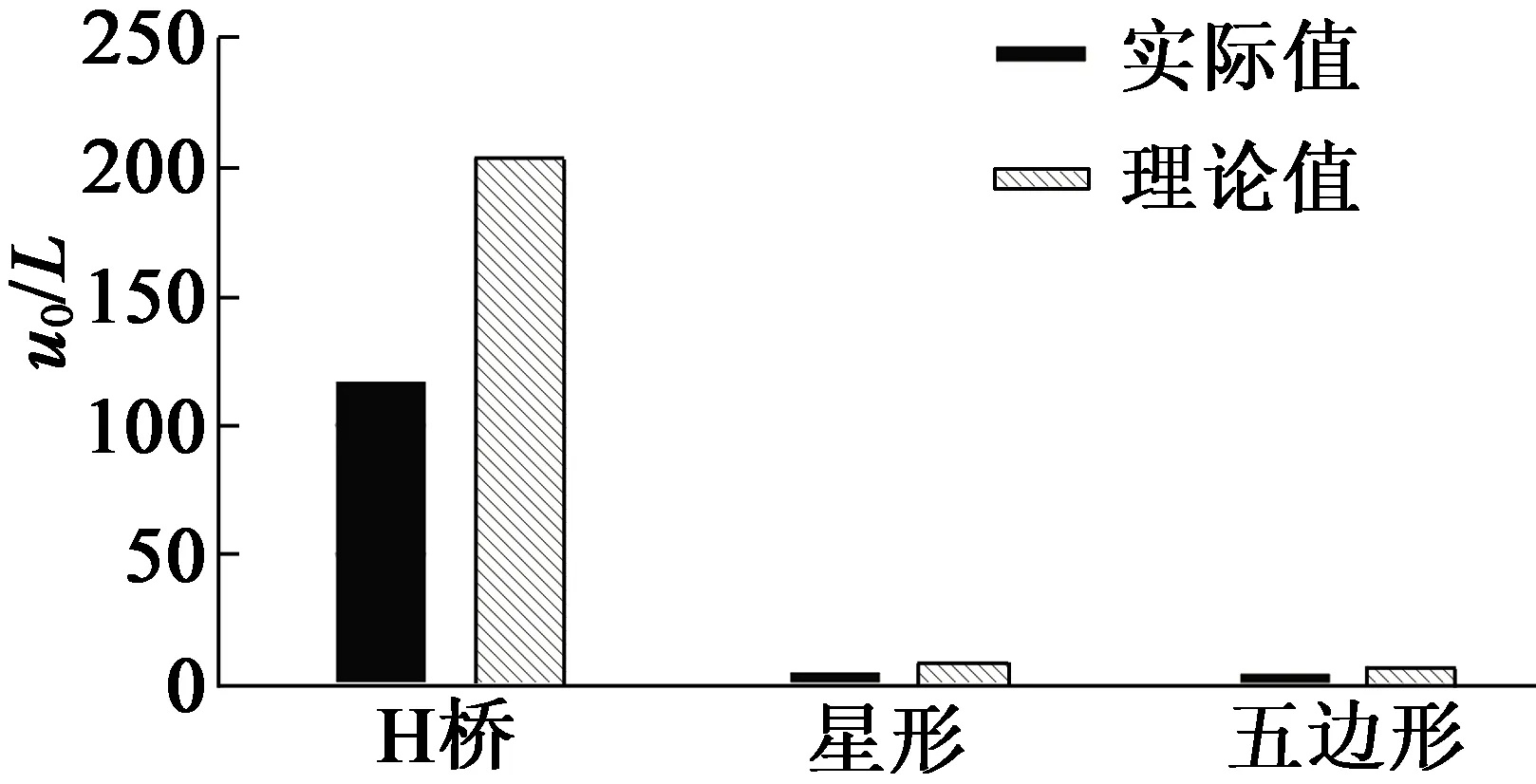
图7 A相电流变化率极限值理论与仿真值

实际仿真中A相绕组的电流波形如图8～图10所示。

从仿真结果可以看出，不同拓扑下实际的电流变化率与理论分析值具有相同的量级。在相同的采样周期下，H桥结构下的电流纹波远远大于其他两种连接，仿真结果中A相绕组电流波形也验证了这一点。

由此可以发现，当五相混合式步进电动机采用多相绕组通电的驱动方式时，电压方程中的电感参数对电流纹波的影响会随着电路拓扑的不同而变化。

本文通过理论分析和仿真，得出以下结论：在采用多相导通的驱动方式时，H桥结构会产生较大的电流纹波，驱动系统会受到较大的电流纹波影响，电机无法正常运行，此结构不适合高精度的五相混合式的步进电动机驱动系统；另一方面，星形连接和五边形连接对电流纹波的抑制有较明显的效果。

图8 H桥结构A相电流波形图

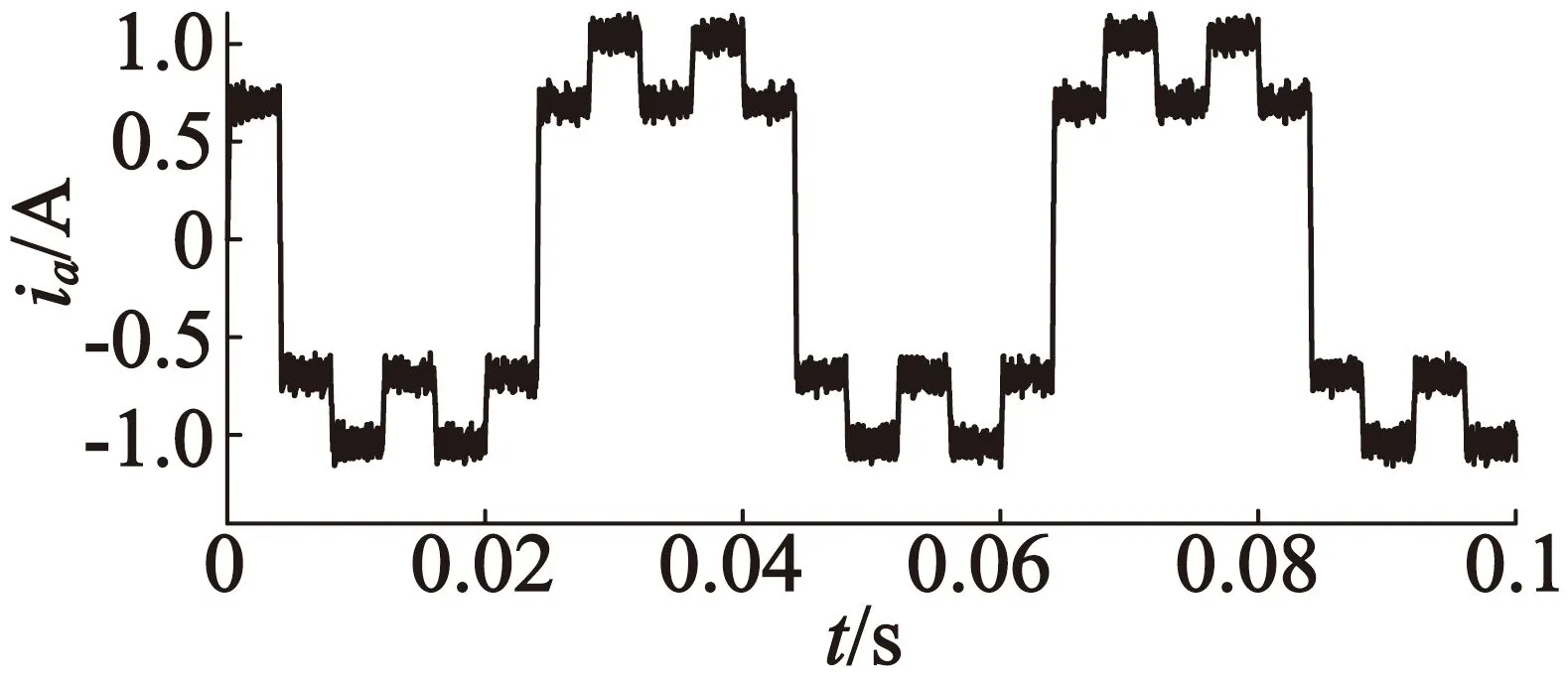
图9 星形连接A相电流波形图

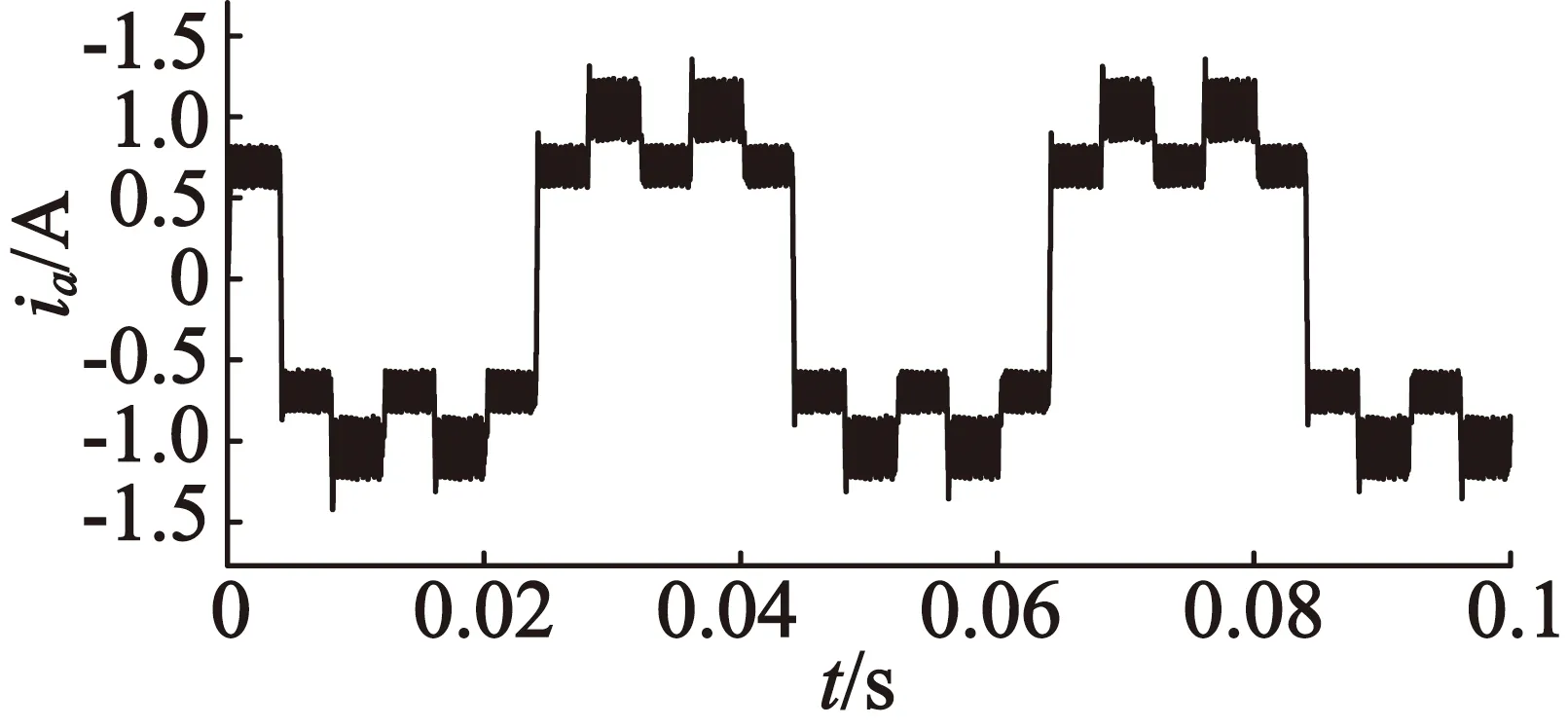
图10 五边形连接A相电流波形图

3.2 实验验证

受实验硬件条件的限制，本文只对H桥和五相半桥星形连接这两种主电路进行了实验验证。本系统的实验所用电机为东方马达公司型号PK569H-B五相混合式步进电动机，实验参数与仿真参数一致。本文所用的实验平台实物如图11所示。

(a) 五相混合式步进电动机

(b) 驱动系统

图11测试平台

采用五相H桥的主电路，A相绕组电流如图12所示。

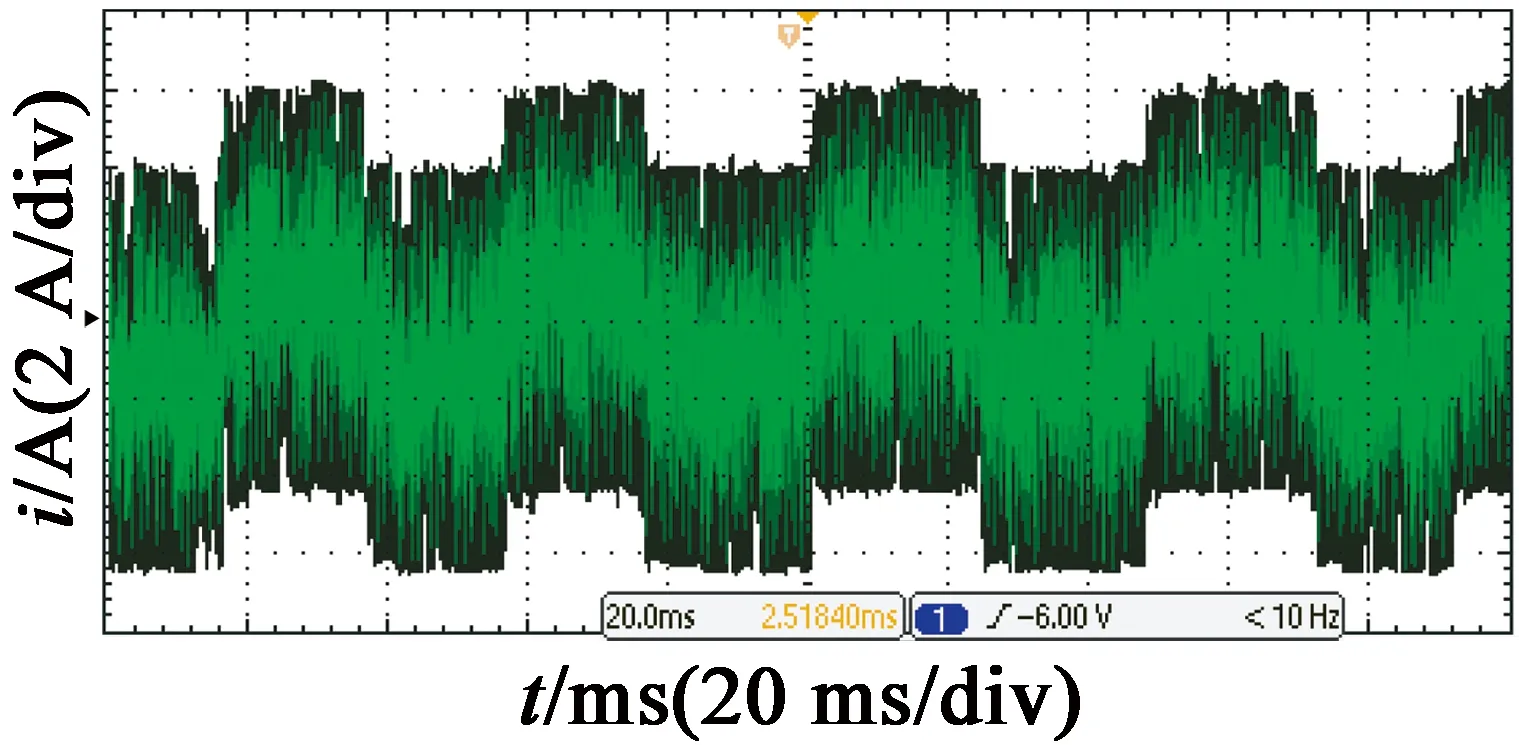
图12 H桥连接A相电流波形图

如图13所示，电流纹波较大，整体来看A相电流已经不能跟随给定，电机振动较大。而且由于电流变化较快，电流经常超过限值，长时间运行会烧坏电机。

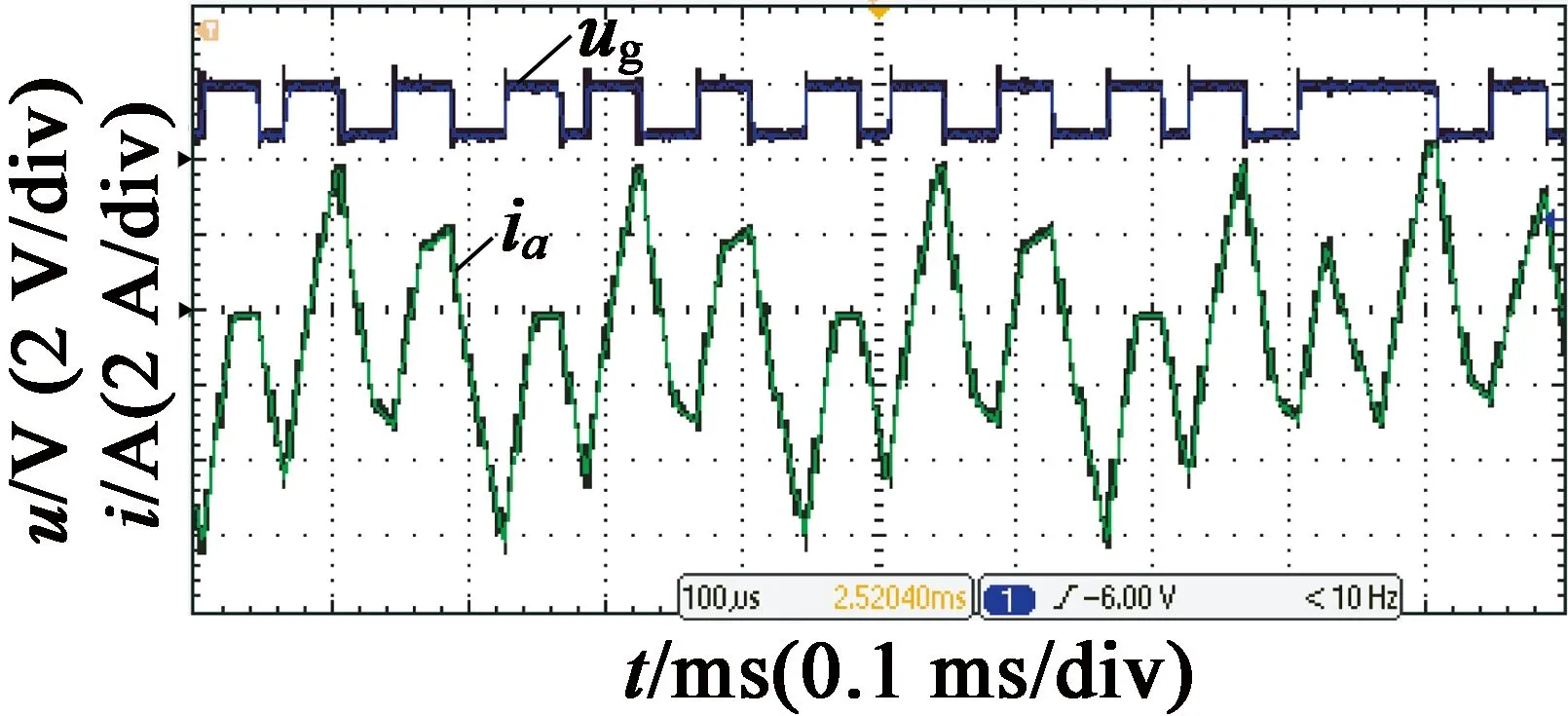
图13 H桥连接A相电流波形细节放大图

一个控制周期内，电流的上升量与下降量几乎相等，且绝对值较大，这也是电流纹波较大的原因，这样的控制效果不能用于驱动电机正常运行。

如图14、图15所示，星形连接时电流纹波相比H桥主电路小了很多，整体来看A相电流能够跟随给定，电机振动较小，运行较为平稳。由于电流变化较慢，电流没有超过限值，不会对电机造成损伤。

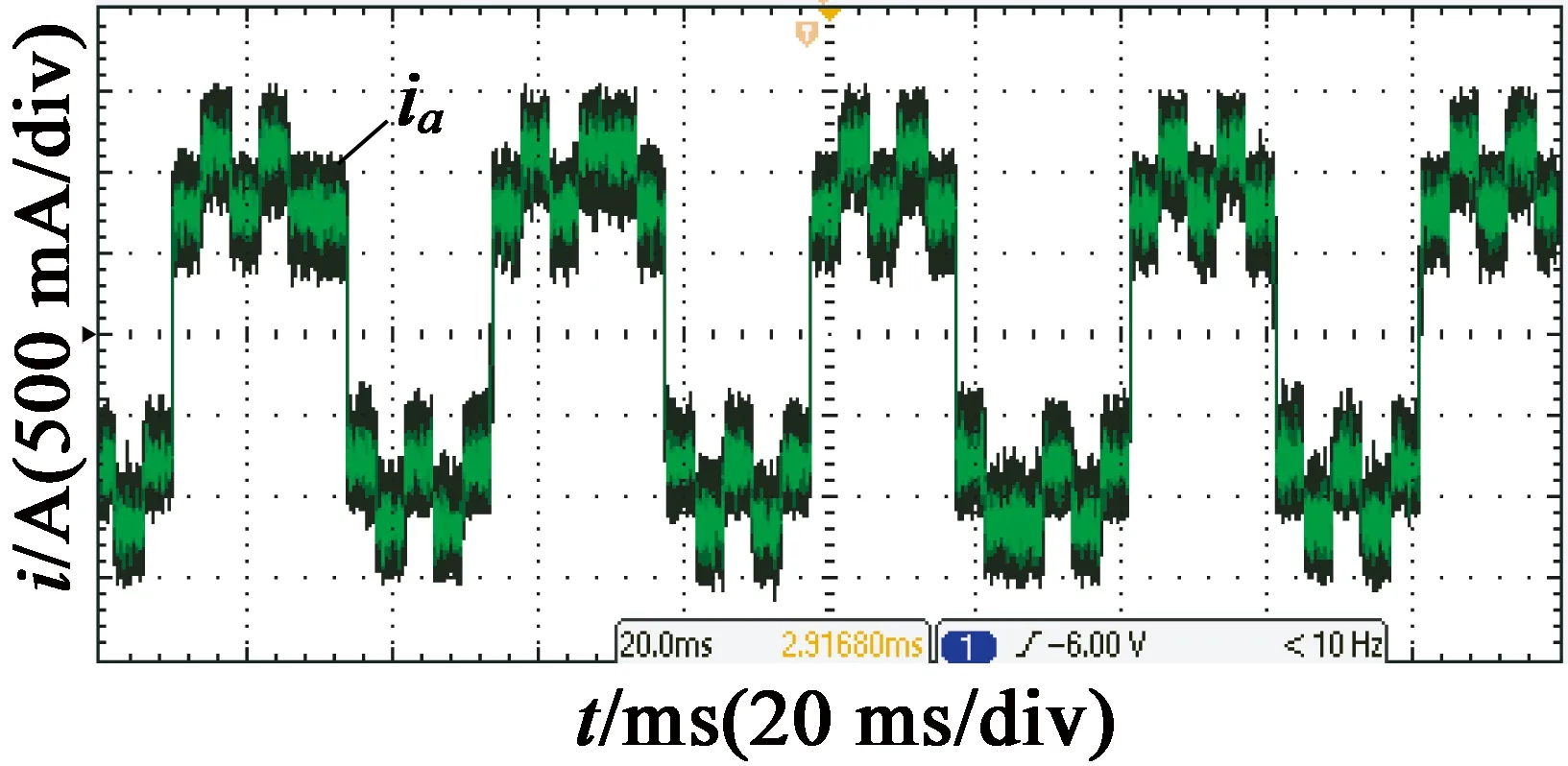
图14 星形连接A相电流波形图

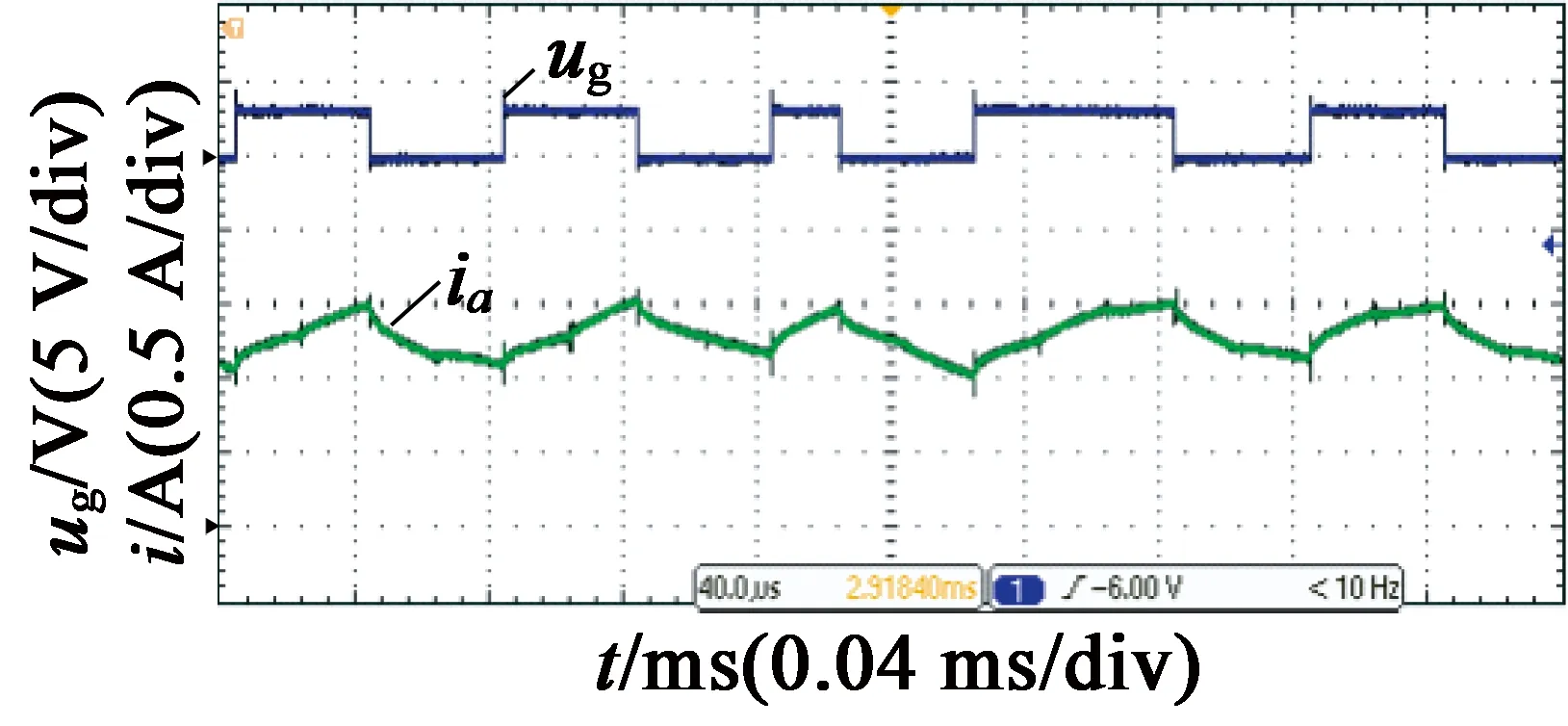
图15 星形连接A相电流波形细节放大图

星形连接时电流纹波较小，电流的上升、下降与A相桥臂上管的开关状态相对应，从图15可以计算出在本次实验中电流变化率的值远远小于H桥结构，这也是五相半桥星形连接主电路下电流纹波更小的原因。

4 结 语

本文研究了五相混合式步进电动机的数学模型，确定了电机的电感参数，对3种常用的主电路进行了对比分析，为进一步研制高性能的五相混合式步进电动机驱动系统提供了思路。推导了3种主电路下定子绕组电压方程组，解算出了电流变化率的表达式，并根据不同的电流控制策略确定了一个周期内电流变化率绝对值的最大值，以此指标来衡量电流纹波的大小。

通过对3种主电路的理论分析、仿真和实验验证可得，对于五相混合式步进电动机驱动系统而言，采用H桥主电路会产生极大的电流纹波，严重影响系统的正常运行；五相半桥星形连接和五相半桥五边形连接能够有效抑制电流纹波，且两者效果接近，可作为五相混合式步进电动机驱动系统主电路的合理选择。