中学数学中的无穷级数问题*

☉广东省佛山市顺德区广东碧桂园学校 李传洲

☉武汉晴川学院计算机学院 杨 艳

一、前言

合情推理是数学里面非常重要的推理方法，它包含归纳和类比两种推理方法，在数学研究中，合情推理常常能帮助我们猜测并发现一个新结论；在证明一个数学结论之前，合情推理常常能为我们提供证明的思路和方向.法国数学家拉普拉斯（Laplace，1749-1827）曾经说过：“即使在数学里，发现真理的主要工具也是归纳和类比.”

但是合情推理所得的结论是需要证明的，这正是数学区别于其他学科的显著特点.美籍匈牙利数学家乔治·波利亚（1887-1985）说过：“合情推理是冒险的、有争议的和暂时的.”合情推理所获的结论，仅仅是一种猜想，未必可靠.例如，法国数学家费马观察到

221+1=5，

222+1=17，

223+1=257，

224+1=65537

都是质数，于是他用归纳推理提出猜想：任何形如22n+1（n∈N*）的数都是质数.这就是著名的费马猜想.半个世纪后，善于计算的欧拉（Euler）发现，第5个费马数

F5=225+1=4294967297=641×6700417

不是质数，从而推翻了费马的猜想.

在中学数学的教学中，类比和归纳的推理方法有着广泛的应用，如数学归纳法、立体几何与平面几何的类比、向量与数的类比、无限与有限的类比等等.本文将着重讨论中学数学的实际教学中无限与有限类比时所产生的问题与困惑，以及如何利用无穷级数来解决所产生的问题.

二、无限求和与无穷级数

在学习有理数概念的时候，我们需要讨论无限循环小数是否是有理数，关键在于无限循环小数能否转化为分数形式.如0.134513451345…能否转化为分数？中学或小学阶段老师所教的将循环小数化为分数的方法如下：

问题1：如何将0.134513451345…化为分数？

解：假设x=0.134513451345…

则10000x=1345.134513451345…

将两个等式相减得9999x=1345

上述方法中让10000x与x的无限小数部分抵消了，思考这样做是否合理？

受到这个问题的启发，有很多学生又提出了新的问题，问题如下：

问题2：“令S＝1+2+4+8+…，则2S＝2+4+8+…，那么S-2S＝1.”到底S与2S谁大？

上述两个问题在计算时用到了同样的方法，但第二个却出现了矛盾，这是为什么呢？如果老师不能合理地解释这两个问题，想必在学生心中教师的权威也会降低不少吧.

本质上，上面两个问题都可以看成是无穷级数的问题.在中小学阶段，由于所学知识有限，只进行有限求和运算，而对于无限求和当然是不涉及的.数学是严谨的，由问题2可知，有限求和法则不一定适合无限求和的运算，那么我们应该如何处理无限求和运算呢？本文关于无限求和运算的讨论主要针对上述两个简单的问题.

定义1：给定一个数列{un}，对它的各项依次用“+”号连接起来的表达式

称为数项级数或无穷级数（常简称为级数），其中un称为数项级数（1）的通项.

数项级数（1）也常写作：或简写为∑un.

数项级数（1）的前n项和，记为

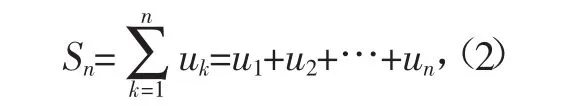
称它为数项级数（1）的第n个部分和，也简称为部分和.

定义2：若数项级数（1）的部分和数列{Sn}收敛于S（即limSn=S），则称数项级数（1）收敛，称S为数项级数（1）n→∞的和，记作S=u1+u2+…+un+…或S=∑un.

若{Sn}是发散的，则数项级数（1）发散.

例1讨论等比级数（也称为几何级数）

的收敛性，其中|q|＜1，a≠0.

回到问题1，可以将0.134513451345…写成无穷级数的形式，

0.134513451345…=0.1345+0.1345×10-4+0.1345×10-8+…+0.1345×10-4n+…

由例1可知，这是一个等比级数，其中a=0.1345，q=10-4＜1，所以该级数收敛且

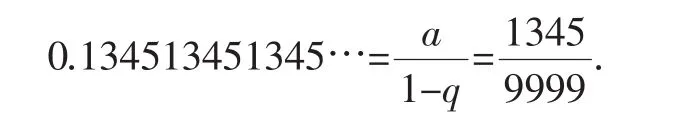
实际上，对于更一般的情形，设一个含有n（0＜n＜+∞）个整数的有限数列：

B={b1，b2，…，bn}，其中bi∈{1，2，…，9}，（i∈1，2，…，n），

则对任意一个循环节不含0的纯循环小数m，均可表示为：

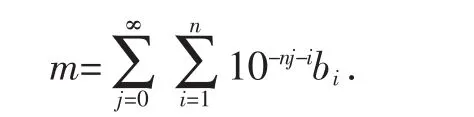
显然m是一个收敛的几何级数，由例1可知，

同理可证任意一个循环节含0的纯循环小数也可化为分数，所以任意的循环小数均可化为分数.

对于问题2，无穷级数S的前n项和Sn=1+2+…+2n-1→∞（n→+∞）发散，故无穷级数S不存在和，所以“S-2S=1”的结论显然是错的.

我们再看一个类似的问题：

问题3：研究级数

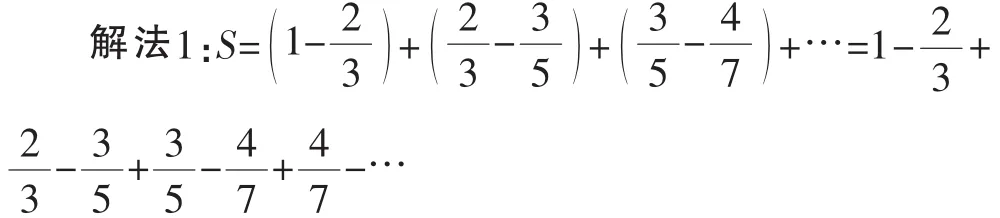
于是，从第二项起全部抵消，故S=1.

括号内从第二项起全部抵消，故

显然，上述两种解法的结果是矛盾的.

对于上述问题中的无穷级数求和问题，若不讨论其是否收敛随便求和，企图用有限求和的计算法则去处理无限求和的问题，这是不严谨的，并且容易出现错误的认知.实际上，对无穷级数的收敛问题讨论得不深入透彻是引发第二次数学危机的原因之一，且引起了长达百余年的混乱.19世纪以来，由于法国数学家达朗贝尔，德国数学家魏尔斯特拉斯（Weirstrass，1815～1897）和法国数学家柯西（Cauchy，1789～1857）详细而系统地提出了极限理论，而后来由德国数学家戴德金（Dedekind，1831～1916），康托（Cantor，1845～1918）等人完善了实数理论，从而结束了长达百余年的混乱，所谓第二次数学危机亦得到解决.

三、结束语

作为新世纪的中学数学老师，需打下牢固的数学理论基础，不断地积累学习数学知识和解决数学问题的经验，不能将对数学的认识仅仅停留在经验水平上，对数学的起源和发展以及发展过程中的矛盾和斗争需要有一个全面的认识，深化并提高对数学具体方法的了解，把握数学家的创造所赖以产生的时代背景以及数学家的这些创造对数学发展的贡献，自觉树立正确的数学观，否则就不能达到全面贯彻数学课程的目标，更不能正确的传播数学思想.