让发现和提出问题成为课堂教学的常态

☉江苏省锡东高级中学 叶 琳

☉江苏省锡东高级中学 谢晓丰

问题背景：

爱因斯坦说：“提出问题在一定意义下比解决问题更重要”.《普通高中数学课程标准（2017年版）》明确提出要培养学生“发现问题和提出问题的能力”及培养“四能”.笔者为此做了统计，在新课程标准中动词“提出”出现了83次，这里的“提出”大多是指“提出问题”.提出问题的前提往往是要“数学地”发现问题：数学地发现问题，就要“用数学的眼光去观察”.课堂教学不仅要关注问题的分析与解决，更要关注问题的源头，即关注问题的发现和提出，将问题的提出作为教学活动的一部分.下面笔者以“一节应用题复习课”为例就如何培养学生发现和提出问题的能力谈谈自己的理解与认识，不妥之处欢迎同行批评指正.

一、给学生创造提出问题的情境

教学片段一：

创设情境，激活思维

数学是刻画现实世界的模型.请观察下列情境：如图1，在半径为R的半圆形钢板上截取一块矩形材料.

问题1：你能提出有意义的问题吗？

生1：矩形面积的最大值是多少？

生2：矩形周长的最大值是多少？

图1

图2

本课从学生熟悉的课本例题出发，引出本课探究的话题.情境是为了数学，活动是为了思考，这就是情境的意义所在.理想的课堂教学就是基于情境让学生发现问题并提出问题，进而产生动力去分析与解决问题.学生提出问题后，着手分析并解决问题，解决后的问题，又成为新的情境（这个情境大多是数学情境），基于数学“进一步”研究的需要，又将提出新的问题，面对这个新的问题，又要分析与解决问题……这就是依托知识发生与发展的线索，形成“提出问题——解决问题——再提出新问题……”的教学结构（如图2所示），基于这样的教学过程，才能培养和发展学生的核心素养.

例如“函数y＝Asin（ωx＋φ）的图象”一节课，笔者给出了如下的设计：给出单位圆上一点P做匀速圆周运动的动画，让学生感受周期运动的规律，体会y=sinx和y=cosx是刻画周期运动的基本模型，再呈现点P在半径为A的圆上，角速度为ω，起始位置为φ的匀速圆周运动（图3），学生发现此时的运动情况更为复杂，但本质上仍然是周期运动，提出问题：如何刻画点P的运动规律？建立直角坐标系，利用三角函数的定义得到点P的横坐标和纵坐标分别为：Acos（ωx+φ），Asin（ωx+φ）.笔者再辅以在自然界、生活和科学技术中俯拾皆是的周期现象，从天体运动到“摩天轮”、车轮转动，再到高科技领域中的振动、波动等，来形象地说明刻画这些现象的数学模型就是函数y=Asin（ωx+φ），显然这是一个新的函数，面对新的情境，学生往往会产生研究的动力，从而自然而然地提出问题：如何研究函数y=Asin（ωx+φ）的性质？通过研究函数的图象，与之有关的数学探究活动也自然而然地展开了.

图3

这节课学生根据数学内部情境自主地提出问题，并进行解答，然后又进一步提出新问题，并得到更深入的解答，从而形成一个螺旋上升、逐层深入的学习过程，培养了学生灵活发散的思维，强化了其解决问题的技能，拓展了其数学感知的能力，丰富并巩固了对数学知识的理解.

好的情境给学生提供了主动提出问题的契机，教师要基于学生已有的经验，选择合适的问题情境，通过问题引领，鼓励学生自主提出想要解决的问题.教师要做“有心人”，注意积累学生提出、发现、解决、理解、拓展的问题或问题串，这些生成性的问题资源能成为很好的教学素材，它更有利于调动学生的学习积极性和参与度.在问题情境的设计中，教师不要设计好所有的问题思路，自己做“向导”，让学生按照预设的路线走，而应该把设计的“天机”有意识地泄露给学生，让学生能体验到提出问题的思路是怎么形成的，慢慢地自己也能成为“向导”.这是一个长期的、循序渐进的过程，教师要经常有意识地做这样的问题引导，鼓励学生提出问题，并验证他们的猜想和结论.长此以往，学生会养成提问题、想问题的习惯，从而激发学生主动学习的自觉性.

二、给学生创造提出问题的机会

课堂教学中几乎时时处处都有很多启发学生提出问题的机会.

教学片段二：

例题解决后教师提出问题：“通过比较，我们发现例题是在引例的基础上对数学背景做了变式拓展，从半圆到优弧，你能做其他的变式吗？”这个问题与问题1相比更开放、更深刻.学生解决了已有的问题，学习情绪高涨，且正处于互相激发的状态，因此便很快提出了一连串的变式：

变式1：在一块圆心角为60°，半径为40m的圆弧上截取一块矩形材料，求矩形面积的最大值.

变式2：如图4，在一块半径为R，圆心角为60°的扇形钢板上截取一块矩形材料，怎样截取才能使这个矩形的面积最大？

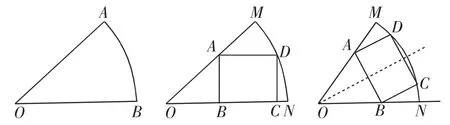
图4

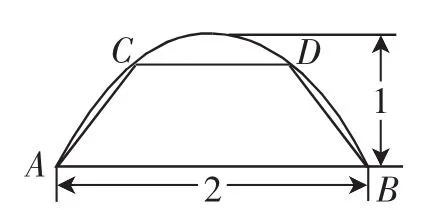
图5

变式3：如图5，一块曲面部分是抛物线形的钢板，其底边长为2，高为1，将此钢板切割成等腰梯形的形状，求梯形面积的最大值.

数学的创新往往始于问题，发现和提出问题是创新的基础.学生精彩纷呈的变式让笔者感到惊喜，说明教师激发得当，学生具有拓展问题和举一反三的潜力，这样的课堂不仅发展了学生的实践能力和创新意识，更能让学生体会到一题多变、以少胜多的教学价值.

笔者认为创新总是和别出心裁、不循规蹈矩联系在一起的，要培养学生主动提出问题的能力，就要允许学生提出不同于教师的甚至是反常态的想法和做法，只有这样才能培养学生的创新精神.事实上学生都是基于已有的知识经验和最近发展提出问题的，大多数是根据已有的问题进行模仿与联系，进而提出问题.只要教师认真钻研，预设充分，一般情况不会游离于问题之外.倘若学生创造性地提出的数学问题超出了教师的预设，笔者认为那更是教学的成功之处.

三、元认知启发引导问题提出

教学中着力突出学生提出问题是落实核心素养的根本.有人会说，如果学生在提出问题这一方面有困难怎么办？这时教师的启发引导就显得尤为重要了.笔者采用涂荣豹教授主张的“启发性提示语引导的原理”设计问题串，以问题为载体，启发引导学生自主参与到学习活动中.教师通过“你能提出有意义的问题吗？”“怎么解决这一问题呢？”“你是怎么想的？”“你说说看具体怎么做？”“你是怎么想到的？”“你还有别的想法吗？”“你能对问题作其他变式吗？”等一系列元认知、认知性提示语，以供给学生“由远及近”的启发.通过问题驱动，让学生的思考层层深入，通过追问的方式，暴露学生的思维过程，并逐步抓住数学知识的本质.

四、关注教学评价，改善教学

教学评价是数学教学活动的重要组成部分.评价要关注学生数学知识技能的掌握，还要关注学生的学习态度、方法和习惯，更要关注学生数学学科核心素养水平的达成.教师要基于对学生的评价，反思教学过程，总结自身经验，发现教学问题，进而改进教学.

教学片段三：

课后，笔者对授课班级的学生进行了访谈.让学生谈谈学习这节课的感受，有学生这样感触：“老师每次请同学回答都会附上一句“你是怎么想到的？”这个问题对于所有的学生来说很重要，我们想知道的不仅是其方法，更想知道方法的源头在哪，老师鼓励我们开拓思维，打破知识的局限，强烈感受到数学的魅力.”有学生这样说到：“这节课让我感受最深的是老师的指导方法，平时因课时有限不太可能像这样一节课只研究一个几何问题，列三个函数式得到三个方程，而且想法不一样的同学可以进行交流，最后殊途同归，这是很好的地方.这样不但有充分的时间进行思考与表达，而且还可以由一个问题解决一类问题，这是平时上课少有的.虽然平时上课老师也会用不同的方法讲一道题，但最终并不会算出同一个结果，有时出现问题重复或者计算太过繁琐而跳过，从而导致学生只能想到一种方法，多方法学数学是好的.”

我们或许可以认为这节课是学生喜欢的课堂，是理想的生态课堂，数学核心素养在学生与情境、问题的有效互动中得到提升.在课堂教学中依托情境，启发学生提出问题，逐步培养学生的数学问题意识，提高学生提出问题的能力，把培养学生的创新意识与创新能力落实到“以问题为纽带”的数学课堂教学之中，才能改变目前“教师问、学生答”的现状，努力变成“学生问、教师答”，并最终演变成“学生问、教师帮、学生答”的理想课堂.