错误，让高中数学课堂更精彩

☉江苏省海头高级中学 孟庆峰

“错误”是指教师与学生认知过程中的偏差或者失误，“错误”伴随着整个教学过程.它有时发生在教师方面，但更多的是发生在学生方面.在课堂教学中，有的教师往往对“错误”讳莫如深，唯恐避之不及，有的老师在教学过程中遇到学生回答错误时，不知该如何是好，尤其在公开课、优秀课评比、观摩课中，追求的是师生的默契配合、对答如流、滴水不漏的效果，稍有闪失，便自责不已，或者抱怨学生配合不好.在高中数学课的教学中，学生回答问题的错误可谓是司空见惯、五花八门，如何处理学生所犯的错误呢？著名特级教师于永正有这样一句话值得我们去深思，他说“课堂上学生犯错误不要紧，只要不犯同样的错误.”把学生的错误当成教育教学的契机，在课堂上抓住学生的错误不放，教师进行再启发和引导，把“错误”当作一种课程资源来开发，并进行分析与讨论、探究，这样能激发学生的求知欲，进而活跃课堂气氛.

一、理解宽容——对待学生错误的感情基础

笔者经常想，高一学生受知识水平的限制，认知过程中出现偏差或失误是正常现象，人非圣贤，孰能无过.即便是老师，其在教学中有时也会犯错误.学生所犯的“错误”是课堂动态生成的内容，是学生真实水平的反映.对学生课堂上生成的错误知识、观点以及看法，倘若进行讽刺、挖苦，甚至大发雷霆、变相体罚，那么失去的将是一个会思考的生命，课堂的生成也就没有了.笔者认为，教师应该以理解宽容的心态对待学生在学习过程中所犯的错误，并找出学生所犯错误的原因，挖掘出可借鉴的知识，不仅让犯错误的学生和其他学生受益，同时也让犯错误的学生在全班学生面前找到了自信.于永正老师有句口头禅：“我最喜欢犯错误的学生.”因此，教师要以发自内心的情感去理解和包容学生所犯的错误，并把这种情感源源不断地注入到学生的心灵之中，学生才能不怕犯错误，才能在犯错误时，大胆展示，真情告白，张扬个性.出错是因为学生还不成熟，哪怕确实有明显的错误，也是正常的，更何况“正确”正是从“错误”的辨析、筛选中逐步形成的；学习是从问题开始，甚至是从错误开始的，有的错误往往是学生对既定思维的反判以及修正.正因为出错，才会有点拨、引导和解惑，才会有研究、创新和超越.教学实践表明：宽容的教育氛围有利于学生的全面成长和个性发展，我们要宽容地、理性地对待学生所犯的错误.不要轻易地否定，而要肯定学生的积极参与，用鼓励的语言去评判.教师要宽容地、理性地看待学生的“错误”.

二、教学机智——对待学生错误的前提

要正确对待学生课堂学习中所犯的错误，还应善于发现并抓住学生的错误.因为在高中数学的课堂教学中，师生思维的碰撞以及情境瞬息万变，学生的想法千变万化，情况错综复杂，随时有可能产生各种意想不到的问题，这需要教师迅速而准确地做出判断，并能对症下药，运用恰当的方法，妥善处理.这就要求教师必须具备教学机智这一基本能力素质.俄国教育家乌申斯基曾说：“不论教育者怎样研究教育理论，如果他没有教学机智，他就不可能成为一个优秀的教育实践者”.

教学机智是指教师成功地处理教学中所发生的意外问题的一种能力.它是建立在教师观察和了解学生的基础之上，是观察的敏锐性、思维的灵活性和意志的果断性的统一.富有教学机智的教师，能及时把学生的“错误”当作生成性的资源，并能恰到好处地利用学生的“认知冲突”，进而围绕教学目标，从多个角度进行延伸拓展，并形成相对完整的知识结构体系，也能在学生的灵魂深处留下较为深刻的印象，这样就有可能创造出教育的奇迹.

案例笔者在讲解必修四三角函数图像与性质的习题课时遇到这样一道题：求函数（fx）=sinx，的值域.笔者没有立即告诉学生应如何求解，而是让学生自己说出答案.

教师：暂时不看甲同学的答案是否正确，这个题目的定义域如果改成x答案又如何？请乙同学继续回答.

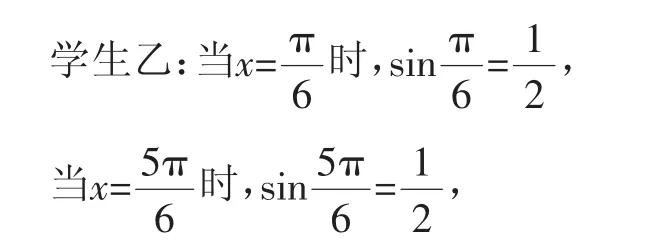
所以f（x）=sinx的值域是……，老师，这个题目是不是有问题？

（全班其他学生哗然）

教师：这个题目没有问题，谁能帮助乙同学解决一下这个问题？

学生丙：这个题目不能简单的代入端点来求解值域，而应该是利用正弦函数y=sinx的图像来解题，因为y=sinx在x不是单调的，所以代入端点这种做法是不正确的，结合正弦函数的图像得出所求函数的值域是

教师：那学生甲的答案是否正确呢？请同学们思考并回答.

学生乙：我知道了，甲同学的答案是正确的，因为给出的定义域正好位于函数的单调区间内，所以通过代入端点来求端点的函数值从而求值域是正确的.

教师：为何有时代入端点正确，有时错误呢？

学生通过讨论得出求函数值域不应通过简单的代入端点来求得.

三、民主氛围——让学生再思考的心理条件

心理学研究表明，人在轻松愉快的环境中，思维活跃，敢于表达自己的看法.学生由于受自身认知水平的限制，回答问题时可能会出现错误.同时又受传统教学思想的影响，学生大多怕老师，对老师存在胆怯的心理，课堂上不敢大胆发言，畅所欲言.怎样让学生在课堂上回答错误后，能够重新再思考、再认识，从而促进学生生命成长、智慧成长、人格成长呢？笔者认为，在这种环境下，教师应该为学生创造一种积极的、安全的心理环境.有了积极的、安全的心理环境，学生学习的热情就会高涨，个性思维就会活跃，人格发展就能和谐，课堂气氛就会有利于发展学生的创造力.教育家陶行知曾说：“只有民主才能解放绝大多数人的创造力，而且使绝大多数人的创造力发挥到高峰.”因此，营造一个民主和谐的氛围，教师和学生才能平等对话，学生才能充分地张扬个性，养成探索未知的情感、态度、信念、动机和需要等.在数学课堂提问中，应允许一部分学生暂时保留自己并不十分完善的认识，通过逐步深入地学习来慢慢领会.教师要以平视的眼光来看待学生，这样学生才能无拘无束地表现自己，从而不怕出错和失败.在课堂中应该努力创设一个优良的课堂气氛，给学生以安全的心理支持和精神鼓舞，把学生的个性、想象以及创造的潜能开发出来.著名教育家赞可夫曾经说过：“我们要努力使学习充满无拘无束的气象，使学生和教师在课堂上都能够自由地呼吸.如果不能营造这样的教学气氛，那么任何一种教学方法都不可能发挥作用.”

四、再启发引导——对待学生错误的方法

教学时，教师如果从学生出现的错误做法出发，进行引导和点拨，不仅能引出正确的想法，还可以“将错就错”，拓宽学生的思维.美国哈佛大学有一句名言：“教育的真正目的就是让人不断地提出问题和思考问题.”问题是探究学习的先导，它既是探究学习的资源，也是探究学习的动力.

案例已知an=n2-λn+2在［2，+∞）上单调递增，求实数λ的取值范围.

学生甲：an是关于n的二次函数，可以采用配方法把求二次函数的参数问题转化为“动轴定区间”问题.an=

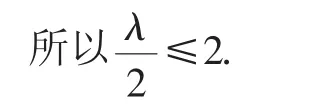
所以λ≤4.

教师：这种解法是否正确，其他同学有没有不同的意见？

学生乙：我认为甲的解法不正确，因为n是有定义域的，且n∈N*，可我不知道该怎么做.

学生丙：这个函数图象是一群孤立的点，横坐标是n，纵坐标是an，结合（n，an）的图象是一群孤立的点，就不难得出（2，a2）是可以在轴的左侧的，只要（2，a2）到轴的距离小于（3，a3）到轴的距离即可，反映在量的关系上即，从而得出正解λ＜5.

教师：本题学生甲错误地认为an是关于n的连续的二次函数，学生甲在解答时没有考虑到n的定义域，事实上n∈N*，本题的实质是数列，且数列是一种特殊的函数，其特殊性在于定义域是正整数集或有限子集，图像是一群孤立的点，横坐标是n，纵坐标是an，倘若学生能考虑到数列是特殊的函数并能透彻地理解其特殊性，再结合（n，an）的图象是一群孤立的点，就不难得出（2，a2）是可以在轴的左侧的，只要（2，a2）到轴的距离小于（3，a3）到轴的距离即可，反映在量的关系上即，从而得正解λ＜5.本题还有其他解法吗？

学生丁：本题还可以转化为“恒成立问题”，即an+1＞an在［2，+∞）恒成立.

即（n+1）2-λ（n+1）+2＞n2-λn+2在［2，+∞）恒成立；

即λ＜2n+1在［2，+∞）上恒成立；

即λ＜（2n+1）min=5；

故λ＜5.

在高中数学课的教学中，教师应创设适当的情境，精心设计问题，以启发学生的思维，推动、激活并延续教学过程.由于学生受已有知识结构、年龄特征、社会经验、能力倾向、个性特点等因素的制约，有时会出现课堂集体失语，思维阻塞，从而导致课堂冷场，或者虽有回答，但是不着边际，可能犯知识性的错误或解题方法上的错误，远离教师的设问所要达到的目标，导致教学过程中断.这时就需要教师运用教学机智来启发并引导学生，融化学生思维的冰层，让课堂重新焕发生机.

记得有一位特级教师说过这样的话：“教1+2=3的老师是合格老师，教1+2=？的老师是好老师，而教1+2=4的老师才是优秀老师！”显然，这位老师的话表达了这样一种思想：“错误”可以激发学生的心理矛盾和问题意识，从而更好地促进学生的认知和发展.这种思想充分体现了新课程理念.叶澜教授在她的《新基础教育》理论中提出了“课堂动态生成”的观点，认为生成性的教学体现了学生的主体地位，展现了课堂教学的真实性.学生的思想以及情感时刻都在变化，高中数学课是不断生成的教学过程，教学中学生所犯的形形色色的“错误”就是一种重要的生成性课程资源，机智地挖掘并运用各种课堂“错误”资源，将给高中数学课堂带来蓬勃的生机与活力，我们的课堂也会因此变得更加精彩.