整合课本与资料 探究与拓展并行*——“直线与圆相切”微专题课堂实录

☉甘肃省天水市第一中学 刘 怡

本节课是笔者参加与兄弟学校同课异构交流活动时所做的课堂实录.教学设计综合考虑高考题的考点，复习资料中学生的难点，课本中的一些经典习题，试图将直线与圆相切的相关知识点有机地整合在一起，设计成适合学生探究性学习的高三一轮复习课.

考情分析：在全国卷文科试题中，直线与圆位置关系中的相切问题是高频考点.试题大多带有综合性，内容涉及对称、定点、定值、最值等题型.试题强调几何问题代数化，代数问题几何化的意识，要求提高应用圆的几何性质以及运用数形结合思想解题的能力.

学情分析：授课班级为高三文科普通班

（1）学生做复习资料题时遇到的难点：对过圆外一点引圆的两切线，求两切点所在的直线方程的这类问题存在解题困难.

（2）对圆的几何性质掌握较差，且缺少探究，在解答直线与圆有关的问题时，偏重代数运算，忽略圆的几何性质，从而将简单问题复杂化.

（3）仅会运用基本方法解答问题，运算过于繁琐，对“设而不求”等思想方法缺乏理解，不会运用.

教学目标：（1）会探究直线与圆相切的相关问题.例如求切线方程、切线长、两切点连线所在的直线方程等.（2）能结合直线与圆相切的几何性质来解决一些最值问题.

重点：过圆外一点引圆的切线，求两切点所在的直线方程.

难点：有关直线与圆相切的最值问题.

一、课堂简录

1.直线与圆相切几何元素的探究

例1 过点O（0，0）作圆M：（x-3）2+（y-4）2=5的两条切线，切点分别为P、Q.

（1）试求切线OP、OQ的直线方程.

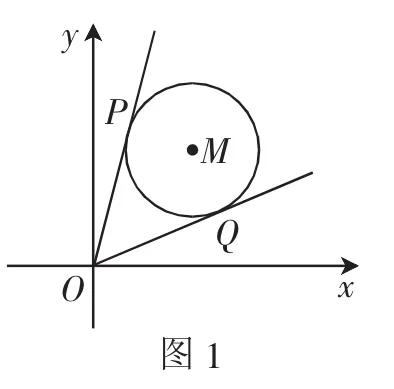
变式2：过点（2，6），求圆的切线方程呢？

让两名学生同时在黑板上解答例1（1）.

生1：设切线方程为y=kx，联立方程得（k2+1）x2-（6+8k）x+20=0，然而在计算Δ=0时出错.

教师点评：学生2侧重几何法，若直线与圆相切，则圆心到直线的距离等于半径，然后用此性质进行求解.学生1侧重代数法，直线与圆的方程联立后，让判别式等于0，进而求得切线斜率.相比而言几何法运算量少，不容易出错.但是联立方程的方法是讨论直线与圆锥曲线位置关系的基本方法，具有一般性.可以迁移到直线与椭圆、双曲线、抛物线相切的相关问题上.

师：变式1先不计算，并思考在解答中和（1）有什么相同和不同吗？

生3：等量关系和前者相同，解题思路也一样.

生4：点都在圆外，要用点斜式设切线方程.

生5：数字比之前的麻烦，并且带有根号.

师：同学们说的这些都对，大家有没有注意到设点斜式的前提是斜率存在，结合图形这个圆有两条斜率不存在的切线，x=3±作出图形），因此，数据代入得到的方程只能求出一条切线的斜率，另外一条就是斜率不存在的x=3-

师：从图形中可以很直观的看出前两题的点都在圆外，那么变式2呢？就不那么直观了，我们可以借助方程来判断.

学生齐声：点在圆上.

生6：因为切线和过切点的半径垂直，故求出切线斜率即可.

师生总结：过一点求圆的切线，首先要判断点与圆的位置关系.若点在圆上则是一条切线；若点在圆外则是两条切线，如若方程此时只有一解，说明另外一条切线的斜率不存在.

（2）求切线OP、OQ的长度.

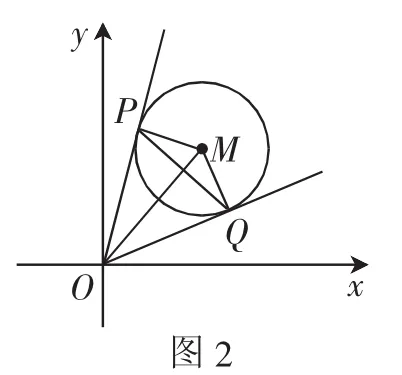
（3）求两切点连线PQ的直线方程.

生8：联立切线与圆的方程，求切点P，Q的坐标，再用两点式求直线方程.

生9：只需求出一个切点即可，PQ和OM垂直，用点斜式更简单.

师：你觉得哪个切点运算简单些？

全班齐声：Q点.

全班动手运算得出结果，PQ的直线方程为：3x+4y-20=0.

师：以上解法是代数解法，记作解法一.注意观察图形，大家还能发现其他解法吗？

生10：因为∠OPM=∠OQM=90°，所以P，Q两点在以OM为直径的圆上，以OM为直径的圆的方程为x2-3x+y2-4y=0，因此PQ是两圆公共弦所在的直线方程.与圆M相减即可得PQ的直线方程.

师：这个方法是几何解法，记作解法二，其运算的确比解法一更为简便.大家还能找到其他解法吗？

全班沉思中，没有学生主动发言.

师：对MP⊥OP也可以用向量构建等量关系.设切点P（x，y），由=0得x2-3x+y2-4y=0，同理Q点也满足此方程，即这个方程是过P，Q两点的圆，以下同解法二.

解法三是解法一和解法二的综合，在此过程中要注重对点的设而不求的解题方法.

例2 （2015年江苏10）在平面直角坐标系xOy中，以点A（1，0）为圆心且与直线l：mx-y-2m-1=0（m∈R）相切的所有圆中，半径最大的圆的标准方程为______.

师：首先要利用数形结合思想，认真作图.并思考这条直线有何特点？什么在变，什么没变？

生齐声：有定点，斜率在变.

师：求定点.

生齐声：（2，-1）.

师：不妨记为点P.

师：因为圆与直线相切，所以圆心到动直线的距离就是圆的半径.利用电子黑板作图软件，绘制直线，并让直线绕着定点P旋转，让学生仔细观察定点A（1，0）到直线距离的变化，让学生直观感受.不一会儿，学生齐声回答，当PA⊥l时，PA

二、课堂小结

这节课我们对直线与圆相切的问题做了一个有机整合，此类题型涉及对称、定点、最值等，同时对相切的几何元素做了一个深入的学习.一般解析几何的解题思路不唯一，我们不要畏惧运算，但更不能死算，在解决圆与直线相切的问题时，要善于分析圆的几何性质，并利用数形结合思想，才能找到更为简便的计算方法.

“不积跬步，无以至千里；不积小流，无以成江海”，最后，希望我们能养成善于对所学知识进行归纳、反思的学习习惯，也祝愿大家在学习的道路上，不断前行.

三、教学反思

高三复习中，学生和教师大都重资料而轻课本，容易陷入题海战术之中，那么复习中如何落实核心素养呢？笔者认为引导学生先把课本复习好，然后再以课本为生长点，让学生体会很多高考题是对课本的变式、综合或者拓展.以课本为生长点，对知识加以整合、探究并拓展，从而达到对知识的深度学习，使复习更高效.整个课堂是师生在对话中交流，在合作中学习，因此课堂气氛自然、流畅.

四、“微专题”的教学思考

1.专题的确定：遵循“真”、“实”、“小”的原则

“微专题”不求面面俱到，而是针对学生在单元复习和大专题复习中暴露出的在知识、方法和能力方面的薄弱环节，选择切口小、角度新、针对性强的小专题，以学生复习中的“问题”促“专题”的生成，力求解决学生学习中的“真问题”和“实问题”.教学设计主要是考虑到以下两点因素：学生的难点和考试的热点.

2.注重知识的整合，突出“以小见大”

“微专题”的教学关键在于抓住课堂内容的主线，让学生在真情境、真讨论、真问题、真思考中学会学习，理清例题之间的内在逻辑关联，这样才能使学生做到“举一反三”，“触类旁通”.F