基于数学学科核心素养的数学课堂教学实效性之探究——以“三个正数的算术—几何平均不等式”教学为例

☉广东省深圳市红岭教育集团高中部 朱达坤

一、提出问题

《普通高中数学课程标准（2017版）》（以下简称“2017年版新课标”）要求高中数学教学以发展学生核心素养为导向，体现育人价值，逐步培养学生形成正确的价值观念、必备品格和关键能力.数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，是在数学学习和应用的过程中逐步形成和发展的.数学学科核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析，这些数学学科核心素养既相对独立、又相互交融，是一个有机的整体.

践行数学核心素养的关键在课堂，通过对课堂教学的研究，对比“2017年版新课标”提出的数学核心素养，从而努力提高数学教学的实效性，在培养学生数学学习兴趣和体会数学的价值上狠下功夫.

我们在教学中自觉对比“2017年版新课标”中核心素养的要求，践行核心素养的六个维度，实施我们的课堂教学实践.下面举例说明，其中的教学内容选自人教A版教材《选修4-5》第一讲第3课时的内容.

二、“三个正数的算术-几何平均不等式”的课堂教学实践

1.课程目标

（1）探索并了解三个正数的算术-几何平均不等式的证明过程.

（2）会用平均不等式求一些特定函数的最大（小）值.

（3）会建立函数不等式模型，并利用其解决实际生活中的最值问题.

2.教学重点

会用三个正数的平均不等式求一些特定函数的最大（小）值.

3.教学难点

会建立函数不等式模型，并利用其解决实际生活中的最值问题.

4.学情分析

学生在学习了“基本不等式”之后，我们要把它进行推广，首先就要推广到关于三个正数的算术-几何平均不等式，而在实际教学过程中，从定理的证明到应用，都比基本不等式的难度要大得多.

5.课堂教学的实施过程

（1）关于定理“已知a，b，c∈R+，那么a3+b3+c3≥3abc，当且仅当a=b=c时，等号成立”的证明.

①课本的证明：因为

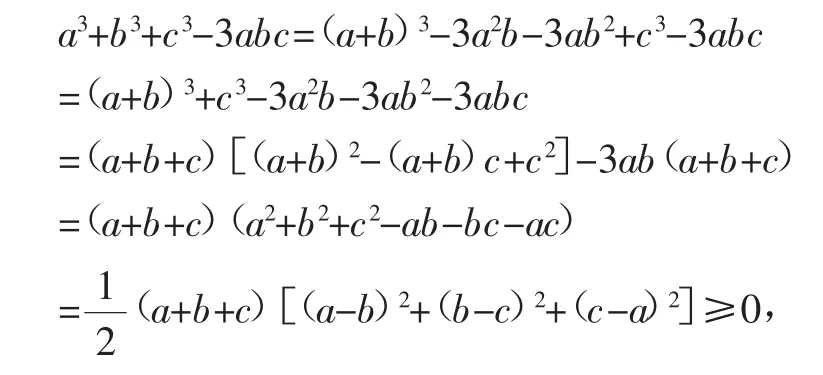
所以a3+b3+c3≥3abc，当且仅当a=b=c时，等号成立.

②证明另法：这是一个循环不等式，我们针对循环不等式可以设计如下的证明方法：因为a3+b3=（a+b）（a2-ab+b2）≥（a+b）ab=a2b+ab2，

同理b3+c3≥b2c+bc2，c3+a3≥c2a+ca2.

所以三式相加得：2a3+2b3+2c3≥a2b+ab2+b2c+bc2+c2a+ca2=a（b2+c2）+b（a2+c2）+c（a2+b2）≥6abc.

所以a3+b3+c3≥3abc，当且仅当a=b=c时，等号成立.

教师发问：以上两种证明方法哪一种同学们更容易接受一些呢？

同学们基本上认为“证明另法”要更好一些，这样对于培养同学们的“逻辑推理”和“数学建模”这两种数学核心素养更有效一些.

③阶段性小结

随着社会的进步，信息化水平越来越高，人类的知识水平不断提升，数学教学改革势在必行，但在学习和传承的时候还是要谦虚好学.在教学中，应该由教师剖析、引导、讲解的地方还是要讲清楚，讲到位，怎么讲好，哪一种方法更符合核心素养、更符合思维规律、更能展现数学的本质，是我们课堂要追求的目标.

（2）定理的分析和需要强调的几点

和基本不等式的推导一样，由定理“已知a，b，c∈R+，那么a3+b3+c3≥3abc，当且仅当a=b=c时，等号成立.”我们得到三个正数的算术-几何平均不等式“定理3：如果a，b，c∈R+，那么，当且仅当a=b=c时，等号成立.”

利用此定理求最值的时候和“基本不等式”一样仍强调“一正、二定、三相等”，这是共性，是具有一般意义的.

（3）定理的应用

①教师通过例题围绕本节课的核心内容进行引导，纠错，建立正确的数学理论.

T（T代表教师，下同）讲解：如果我们利用基本不等式变形为，可以求出最值吗？

S（1S代表学生，下同）：不可以，因为右边没有出现定值.

T讲解：很好！那么应该怎样分拆3x呢？

S（3举手回答）：把3x分成相等的就可以了.

②教师再通过其他例题调动起学生的主观能动性，把学生的主体作用慢慢挖掘出来.

三、回顾与反思

1.从数学的核心素养出发营造我们的教学环境

“2017年版新课标”提出的六大核心素养应该成为我们课堂教学目标实施的核心目标.教学内容是培养学生数学核心素养的载体和土壤，教材和课件是培养学生核心素养的重要资源，教学形式和方法是培养学生数学核心素养的关键手段，吃透教材，理解好教学内容，那么在教学设计中落实学生的核心素养就有了固着点，在教学实施中培养学生的核心素养就有了生长点.

在上面“三个正数的算术-几何平均不等式”的课堂教学实践中，笔者没有拘泥于课本，没有照本宣科地讲解课件的内容，而是围绕本节课的重点和难点讲清理论，给出直观的正确的定理和解题模式，循序渐进，进而悄悄地把学生作为课堂的主体地位凸显出来，老师的主导作用仍然在起作用，通过讨论、质疑、纠错，使学生将“一正、二定、三相等”的知识脉络深深的植根于脑海中，从而实现了对“数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析”的培养.

2.从数学的核心素养出发提升我们课堂教学的实效性

数学核心素养的关键在课堂.本节课内容多，信息量大.如何在保证学生充分活动和思考的基础上突出重点，突破难点，这些都是老师在备课中要认真思考和准备的.学生的课堂收获关键在于思维的收获，在理解基础上的记忆会更加深刻.课堂教学活动的设计既要以学生的角度去认识、理解所教授的知识，又要站在思维的高度、理论的高度来统领课堂，这样的课堂对于学生而言才具有实效性，才是一个高效有用的课堂.

教无定法，学无止境.但教学的一般规律还是有的，笔者认为提高实效性可以大致从以下几个方面思考：（1）注意提问的针对性和辐射面；（2）注意为学生提供思考问题的时间和空间；（3）创设民主、和谐的课堂教学氛围；（4）关注学生课堂学习的参与度；（5）运用多种教学手段，丰富课堂教学内容；（6）教师应加强个人的综合素养的提高，用自身的魅力感染和影响学生.

四、结束语

任正非说：“中美贸易战的根本问题，是教育的问题；芯片问题，光砸钱不行，要砸数学家、砸物理学家.”由此看来，中国的数学教育的提升和改革迫在眉睫，势在必行.而无论怎么改，数学教师都必须明了数学的本质，也就是核心素养，而核心素养的培养关键在课堂，因此要提高课堂教学的实效性，把握好课堂节奏，不满堂灌，不将课堂教学模式化，不唯分数论.潜心研究数学教学，让学生体会“数学好玩”，进而“玩好数学”，这样距离我们“中国梦”的实现就不远了.F