变中有度 变中求活——例谈变式教学的层次

☉江苏省江浦高级中学 经中进

“变式”原来是心理学上的一个名词，其意义是变换材料的出现形式.而引入到数学教学中，变式教学已经成为了一种备受认可且非常常用的课堂教学模式.无论是新授课还是复习课中都有变式教学的影子，其可以很好地夯实学生的数学基础，培养学生灵活解决问题的能力，提升学生的发散性思维与创新意识，并有着非常好的教学效果.

一、变式现状

然而，数学变式教学在实际应用中，有时效果并不佳，其只是表面形式上的机械变式，最多只是重复训练，能力层面上的突破并不明显.数学变式教学缺少深度、广度、灵活度.

变式教学必须是一个循序渐进的过程，通过变式教学突出数学知识、能力、方法的本质属性，突出问题解决的思想性，有效提升学生举一反三和灵活创新的能力，这样的变式教学才能充分凸现其价值，才能充分提高学生的能力，培养学生的核心素养.

变式教学要形成效益，就得从变中有度，变中求活等方面做文章.下面结合一道圆锥曲线问题的变式教学设计来进行多角度阐述.

二、案例分析

【高考在线】（2018·全国Ⅲ卷理·11） 设F1、F2是双曲线=1（a＞0，b＞0）的左、右焦点，O是坐标原点.过点F2作C的一条渐近线的垂线，垂足为P，若则双曲线C的离心率为（ ）.

分析：根据题目条件，利用双曲线中参数a，b，c的几何意义可知|OF2|=c，|PF2|=b，进而利用勾股定理可得|OP|=，再借助解析几何中的直线方程来转化，从而得以建立参数a、c之间的关系式，并求解出双曲线的离心率.

解：由参数a，b，c的几何意义可知|OF2|=c，|FP2|=b，则有，可得

结合两直线垂直的关系，可得直线PF2的方程为y=（x-c）.

而F1（-c，0），由两点间的距离公式可得|PF1|=.整理可得c2=3a2.

故选择答案：C.

点评：解决圆锥曲线的离心率问题的关键是寻找椭圆或双曲线中参数a、b、c所满足的关系式，对此有两种常见的破解方式：一是利用几何特征、几何运算来得到相应的关系式；二是直接利用代数运算来建立关系式.往往利用几何特征来处理会减少一些运算量.

三、变式过程

1.同层变换，加深解法印象

此类变式属于同层变换，对问题加以适当变换，与原来题目的难度基本相同，解法也基本相同，这样可以更有效地帮助学生加深对此类问题的解法印象，形成解题模式.

【变式1】（2019·浙江模拟）设F1、F2是双曲线1（a＞0，b＞0）的左、右焦点，O是坐标原点，过点F作C2的一条渐近线的垂线，垂足为P，若|PF1|=2|PF2|，则双曲线C的离心率为______.

解析：由a，b，c的几何意义可知|OF2|=c，|PF2|=b，则有|PF1|=2|PF2|=2b.

结合两直线垂直的关系得直线PF2的方程为y=x-c）.

2.浅层变换，深化概念理解

此类变式属于浅层变换，是在学生掌握相应解题方法的基础上，引导学生从本质上回归到基本概念、基本知识与基本技能，克服思维定式，初步形成掌握此类基本方法破解问题的能力.

【变式2】（2019·江苏模拟）已知双曲线（a＞0，b＞0），过双曲线C的右焦点F作C的渐近线的垂线，垂足为M，延长FM与y轴交于点P，且|FM|=4|PM|，如图1所示，则双曲线C的离心率为______.

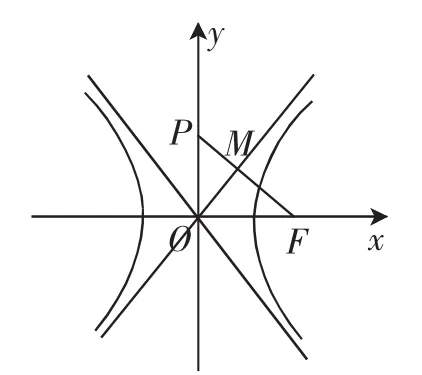
图1

解析：设F（c，0），可知双曲线C的渐近线方程为

3.中层变换，突出思维能力

此类变式属于中层变换，是在学生初步形成掌握此类基本方法破解问题的基础上，真正学会分析问题、处理问题与解决问题的能力.

【变式3】（2018届山东省泰安市高三二模·12）已知F为双曲线（a＞0，b＞0）的右焦点，过点F向C的一条渐近线引垂线，垂足为A，交另一条渐近线于点B，若|OF|=|OB|，则C的离心率是（ ）.

解析：设双曲线C的一条渐近线方程为，则直

由|OF|=|OB|可知△OFB为等腰三角形，则D为BF的中点，可得点B到x轴的距离为点A到x轴的距离的2倍，即，整理可得a2=3b2.

故选择答案：B.

四、反思总结

变式教学要有“度”，变式教学要有“活”，不能只是重复训练的教学，只有渗透数学知识、贯穿数学思想、揭示数学本质的变式教学，才是有价值、高效的教学.因此，教师需要不断加强自身修养，提升对数学知识方法和数学问题的理解程度，从更高层面上去把握问题，只有这样，才能“变出”有“度”、有“活”、有思想、有灵性的题目，从而真正提高数学课堂的效率，培养学生提出问题和解决问题的能力，使学生的发散思维能力、探究能力、创新能力等均得到有效提高.F