二维地基波阻板隔振的复变函数解

周凤玺， 郑 琦

(1. 兰州理工大学 土木工程学院，兰州 730050； 2. 西部土木工程防灾减灾教育部工程研究中心，兰州 730050)

随着城镇化建设和现代工业的迅速发展，各种振动问题日益频繁，环境振动已经成为一种新形式的环境污染，并被列为当前世界的七大环境公害之一。而随着人们生活水平的提高，对生活环境和工作环境的质量要求也越来越高，对振动的限制越来越严格，环境振动及其治理已经成为岩土工程的一个研究热点问题。

自Woods[1]通过一些现场原位试验，研究了近场主动隔振和远场被动隔振的隔振效果，并且提出了一个评判屏障隔振效果的重要参数振幅衰减系数以来，国内外学者对连续屏障和非连续屏障的减振隔振效果进行了一系列的研究工作。比如在振源或需保护结构地基中设置隔振屏障(比如空沟、多排桩、空心管桩等)来降低其振动水平是目前进行地基减振隔振的主要措施[2-5]。由于受表面激振的层状地基中波的传播存在截止频率，当激振频率低于截止频率时，地基中不存在波的传播现象。基于此现象，Schmid等[6]建议使用一个刚性层来形成有限尺寸的人工基岩，并将这个人工基岩称为波阻板(Wave Impeding Block,WIB)。随后他们采用二维频域边界元法，分析了WIB主动隔振和被动隔振，结果表明WIB的被动隔振效果好于填充沟。采用边界积分方程法，Peplow等[7]研究了二维双层地基波阻板主动隔振的隔振效果。利用边界元和有限元法，Takemiya[8-9]研究了WIB的隔振效果。基于层状介质中土与结构动力相互作用的半解析边界元法模型，高广运等[10-11]分别分析了二维和三维层状地基中波阻板的隔振效果。随后，针对三维竖向非均匀和饱和地基模型，高广运等[12-13]对轨道交通荷载作用下竖向非均匀地基和饱和地基中波阻板的隔振性能进行了研究。李宁等[14]通过现场试验，先研究了水平激振下混凝土材料的WIB对层状地基的隔振效果，又分析了WIB的埋深对隔振效果的影响，并对比了实测的位移结果与半解析边界元方法计算的结果。基于Biot多孔介质波动理论，结合PML边界条件，高贝贝[15]用时域有限元方法研究了二维地基中储液多孔波阻板的隔振性能。基于Biot多孔介质波动理论和功能梯度材料，周凤玺等[16-17]研究了含液饱和多孔波阻板和梯度波阻板的地基振动控制研究，结果表明含液饱和多孔波阻板和梯度波阻板的地基隔振体系更加具有优越性。利用傅里叶级数展开的方法，引入辅助函数和波函数展开技术，张海等[18]研究了弹性半空间中含直边界半圆形衬砌隧道对SH波的散射解析解。结合Green函数法及裂纹“切割”技术，采用保角映射的方法，杨在林等[19]研究了SH波下方入射时半无限空间界面附近椭圆形弹性夹杂及任意位置直线裂纹对SH波的散射问题。

由于WIB隔振设计属于土与结构动力相互作用问题，由于其复杂性目前常用的分析方法主要是数值模拟(边界元法、有限元法)和试验验证。但是，对于WIB隔振性能的解析分析较少。因此，本文借助复变函数的积分变换法将有限长度的波阻板变换为单位圆，建立了二维弹性地基中矩形波阻板对波场散射问题的控制方程。考虑平面SH波入射，运用波函数展开法得到了二维地基波阻板隔振性能的解析解答。通过数值算例，分析了波阻板剪切模量、波阻板埋深、弹性波入射角度对隔振效果的影响。

1 WIB的保角映射变换

根据复变函数理论，通过映射函数z=ω(η)可将波阻板所在z平面上所占的区域变换为复平面η上的单位圆，保角映射前后的坐标系统如图1所示，其中H表示WIB埋置深度，α表示SH波入射角度，相应的保角映射公式为[20]。

(1)

式中：

c1=cos(2χπ)

(2a)

(2b)

(2c)

(2d)

式中：χ为取决于WIB长宽比a/b的系数；系数c1∶c7仅与χ有关；R为与WIB尺寸有关的实数，可由以下两式中的任意一式计算：

(3a)

(3b)

对于正方形，即长宽比a/b取1时，χ=0.25；而其他矩形，可采用试算法求χ，即估计一个χ值，由式(2)求得c1∶c7，代入式(1)可得映射函数，它是一个微曲的矩形。以宽度0.4 m，长度4.0 m的WIB为例，经试算得到χ=0.106 5，图2给出映射波阻板以及与单位圆的对应关系，将矩形波阻板所在z平面上所占的区域变换为复平面η上的单位圆。

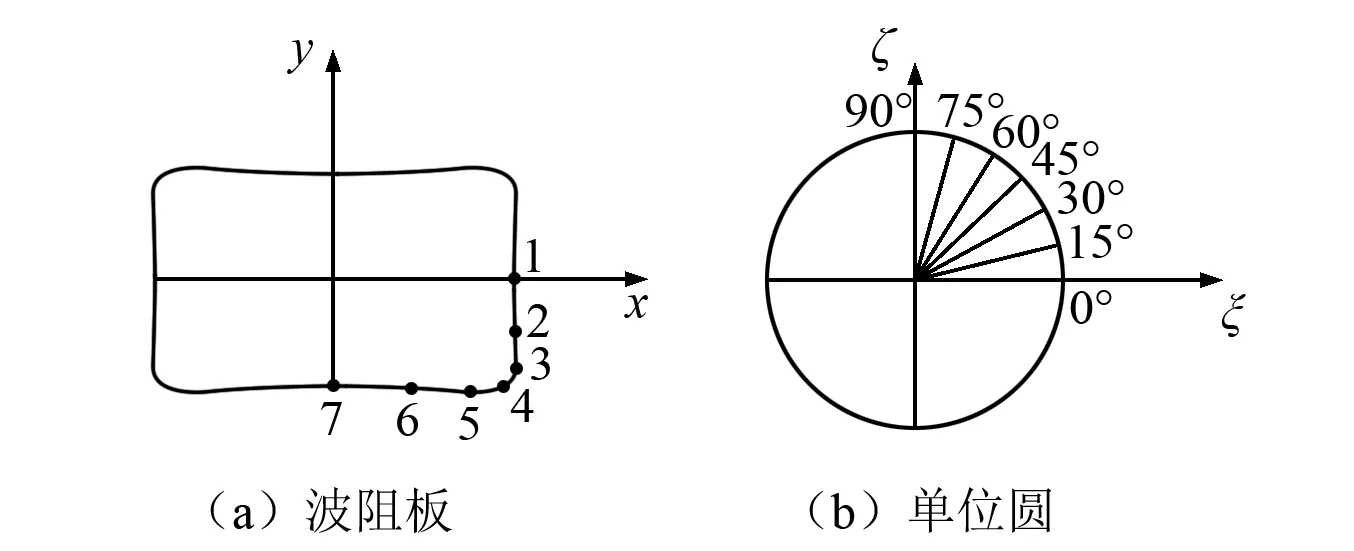
图2 映射波阻板与单位圆的对应关系

2 控制方程

稳态平面SH波入射含WIB的二维弹性地基中，引起了散射波位移场为垂直xy平面的位移分量w(x,y)(省略了时间因子e-iωt)，且应满足Helmholtz方程：

(4)

应力和位移的关系为：

(5a)

(5b)

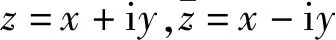
(6)

(7a)

(7b)

而在复坐标系中，应力表达式为：

(8a)

(8b)

式中：θ为曲线坐标系(r,θ,z)中r轴与直角坐标系中x轴之间的夹角。

3 WIB对SH波的散射

3.1 入射波场

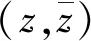
(9a)

(9b)

式中：w0为入射波的波幅；α为入射角；kS为波数。

由(7)可知w(i)和w(r)相对应的应力场为：

(10a)

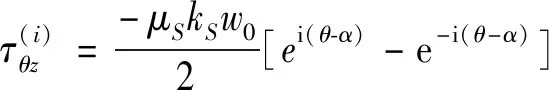
(10b)

(10c)

(10d)

3.2 散射波场

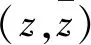
(11)

由式(7)可得到散射波对应的散射应力场为：

(12a)

(12b)

同理，WIB结构内的散射波为：

(13)

所对应的应力场为：

Jn+1(kB|z|)(z/|z|)n+1e-iθ

(14a)

Jn+1(KB|z|)(z/|z|)n+1e-iθ}

(14b)

3.3 边界条件

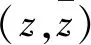
(15a)

(15b)

3.4 问题的解答

将式(9)，式(11)和(13)代入式(15a)，整理后可得

(16a)

将式(10)，式(12)和式(14)代入式(15b)，可得

(16b)

用e-imθ乘方程(16)的两边，并在区间(-π,π)上积分，则得到关于待定复系数An和Bn的理论解的无穷线性方程组：

(17)

其中：

利用截断有限项的方法解出方程组(17)。就可以确定波函数中未知系数An和Bn，并将未知系数An和Bn代入式(9)、(11)、(13)，即求得弹性半空间介质的位移场和WIB的位移场。

4 分析讨论

为验证本文解答的正确性，选取王贻荪[22]对Lamb问题的解析解答。利用突加力问题的闭合解求得了Lamb问题的解答，避免了对难以积分形式解的求积。取弹性地基密度ρs=2×103kg/m3，剪切波速为cs=200 m/s，固有圆频率为ω=10 Hz，剪切模量为μS=80 MPa。对比结果见图3。由图3看出，本文计算值与文献[22]结果相一致，说明本文的算法有效。

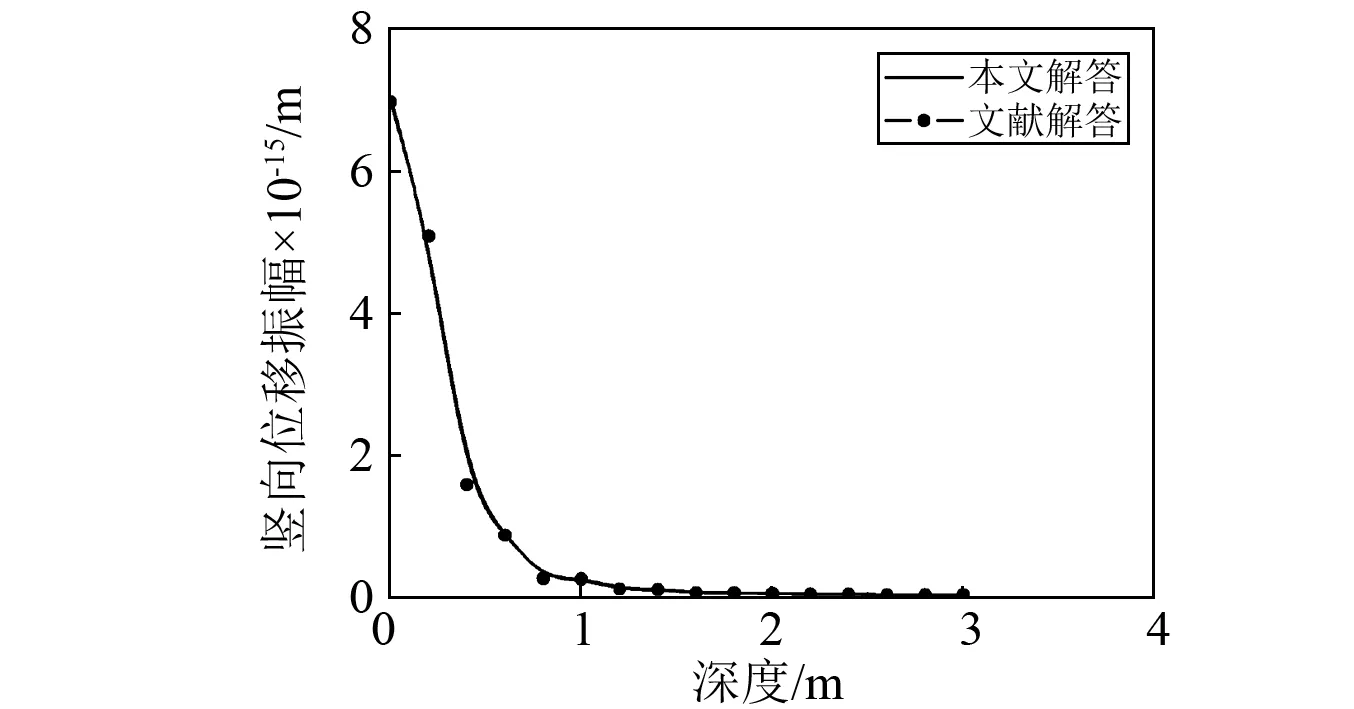
图3 SH荷载激振地表振幅解答对比

对于WIB隔振效果的评价，Woods提出用振幅衰减系数AR来衡量[1]：

AR=有屏障时振幅/无屏障时振幅

且AR≤0.25时隔振效果较好。

为了分析级数项系数对数值计算结果的影响。选取参数a=4 m，b=0.4 m，ρS=2×103kg/m3，ω=10 Hz，μS=80 MPa，kS=0.05，kS/kB=1/3，μB/μS=2，H=0.5b，α=30°。图4给出了不同n的情况下地表竖向位移振幅的变化曲线。由图4知，当散射波系数n取10时可以满足计算精度要求。

分析剪切模量比对隔振效果的影响，选取a=4 m，b=0.4 m，ρS=2×103kg/m3，ω=10 Hz，μS=80 MPa，kS=0.05，kS/kB=1/3，H=0.5b，α=30°。图5绘出了地表振幅衰减系数的变化曲线。由图5知，当WIB的剪切模量与地基的剪切模量比为μB/μS=0.5时，采用WIB隔振体系隔振效果不是很明显，当剪切模量比为μB/μS=1时，可以看出WIB有显著的隔振效果；当μB/μS=2时，隔振效果显著增强。所以，应根据隔振设计实践的需求，合理地选择WIB的剪切模量可以有效提高隔振效果。

图4 竖向位移振幅的变化曲线

图5 不同WIB剪切模量时振幅衰减系数AR变化曲线

其余参数不变，取模量比μB/μS=2时，图6给出了WIB的埋深对地表振幅衰减系数的变化曲线。从图6可以发现，随着埋深的增大对地表振幅的隔振效果减小。

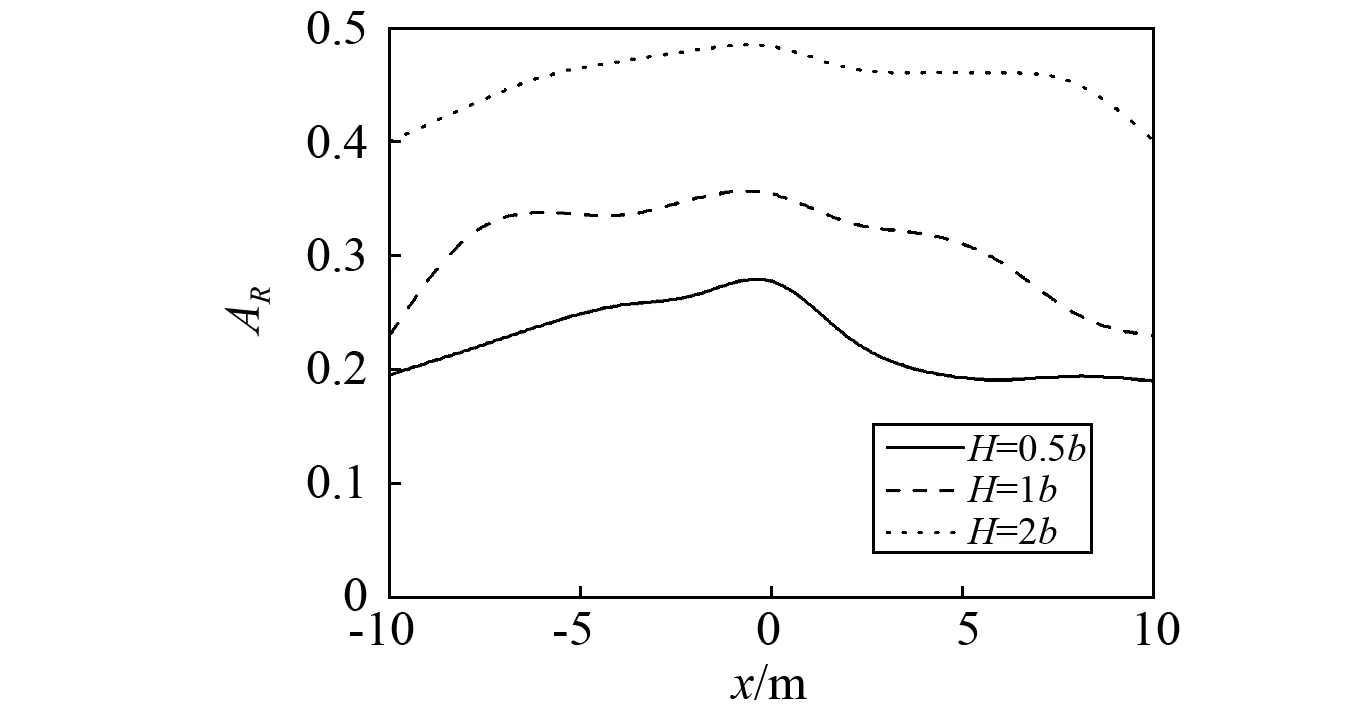
图6 不同WIB埋深时振幅衰减系数AR变化曲线

为了讨论了不同的入射角度变化对地表幅值的影响。图7给出了kS/kB=1/3，H=0.5b时地表振幅衰减系数的变化曲线。由图7知，地震波入射角度α对隔振效果有着明显的影响，随着入射角度的增大隔振效果明显减小，当α=90°时，隔振效果减小尤为明显。

图7 不同入射角度时振幅衰减系数AR变化曲线

5 结 论

运用复变函数的保角映射方法和波场势函数展开法，得到二维弹性地基WIB隔振的解析解答，通过参数分析讨论了WIB剪切模量、埋深、弹性波入射角度对隔振效果的影响，研究表明：随着WIB剪切模量的增大其隔振效果明显增加，随着WIB埋置深度增加隔振效果逐渐减小，并且WIB的隔振效果随弹性波入射角度的增大而减小。