光束通过三棱镜的偏折情况再探讨*
2020-05-18秦琴琴胡志娟
秦琴琴 胡志娟
(上海师范大学数理学院 上海 200234)
三棱镜是一种基本的光束转向元件和色散元件,在光学基本实验中有诸多应用.教材中给出了棱镜最小偏向角θ0的计算[1],并提出可利用公式
(1)
计算棱镜材料的折射率.
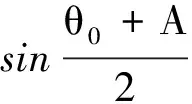
本文详细讨论了光束通过三棱镜的多种偏折情况,给出了三棱镜的顶角和折射率的取值范围对光线是否能从出射边界射出,以及出射光线的偏折情况的影响,并进一步分析了光线的偏向角与折射率、顶角的关系,给出了确定最小偏向角的方法.
1 三棱镜对光的偏折情况
如图1所示为一个顶角为A,折射率为n的三棱镜侧面图.
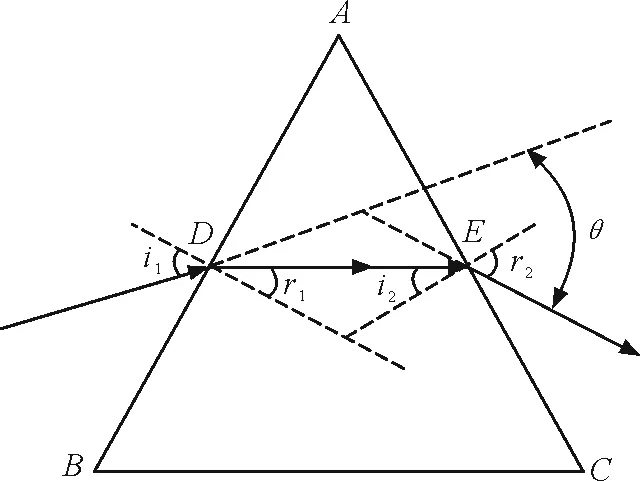
图1 三棱镜侧面图
光线从AB边的D点射入三棱镜并发生折射,到达AC面上的E点,再经过一次折射后从E点射出,两界面的入射角和折射角分别为i1,r1和i2,r2,θ为AC面上的出射光线和AB边的入射光线之间的夹角,即偏向角.
图1中,由折射定律和几何关系有
(2)
A=r1+i2
(3)
由折射定律可知,当入射角i1减小时,r1会随之减小,光线DE会向底面BC偏移,i2会增大.若三棱镜的折射率和顶角满足一定条件,当入射角i1减小到某个值时,三棱镜中的折射光线DE在AC面上发生全发射,如果继续减小入射角,则三棱镜中的折射光线均会在AC面上发生全发射,可见要在AC面上得到出射光线,入射角存在一个最小值.
在教学中有的学生会认为,光束经三棱镜两次折射后的传播方向一定是偏向底面BC的,实际上还可能出现图2所示的情况.当入射角i1逐渐增大时,光线DE在AC面的入射点E会向顶角A移动,这时在AC面的入射角i2将减小.对于材料的折射率不是很大,顶角也不是很大的三棱镜,随着入射角i1的增大,会出现i2=0的情况,继而,光线DE会出现在AC面法线的下方,那么出射光线就会向AC面法线的上方偏折.此时,经三棱镜出射的光线的传播方向并非向三棱镜的底座偏移,而是偏向顶角射出,但出射光线相对于原入射光线仍是向底面BC偏折的.
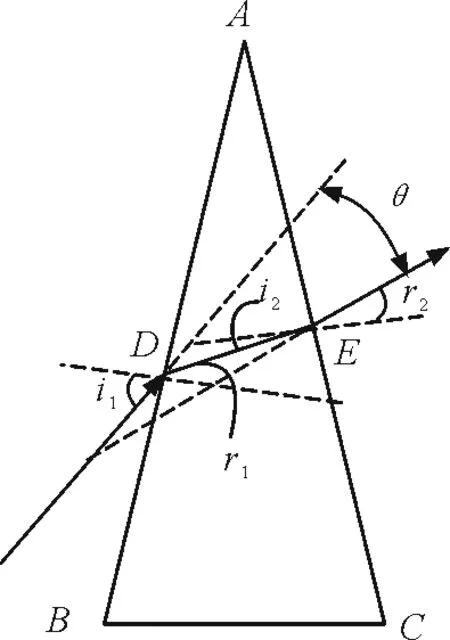
图2 出射光线偏向法线上方
2 入射角i1 折射率n以及顶角A对出射光线的影响
设折射光线DE在AC面上恰好发生全反射时,对应的光线入射角为最小入射角i1min,此时,AC面上发生全反射的临界角满足
结合式(2)、(3)可得最小入射角i1min、折射率n及顶角A的关系为
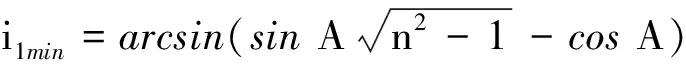
(4)
从式(4)中可以看出,AB边上的入射光线的最小入射角i1min与棱镜折射率n、顶角A均有关系.在折射率n不变的情况下,顶角A越大,i1min也越大.当A增大到某一特定的值,i1min可能增大到90°,这种情况下,从AB边上以任意角度入射的光线,都会在AC面上发生全发射,设顶角A的这一特定值为Amax,那么,棱镜的顶角A超过Amax后将不会从AC面上得到出射光线.利用
i1min=90°
并由式(2)、(3)可求得
因此,给定三棱镜的折射率n=2.4时,则对应的Amax= 49.2°,所以当顶角A=60°,已经超过了有光线出射时要求的最大顶角值,因而不会有光线从AC面射出.
此外,若顶角A越小,i1min也会越小,当A减小到某值Amin,i1min会减小到零,此时恰好所有入射光线都可以从AC面射出.利用
由几何关系可得
而对于顶角A小于极小值Amin的三棱镜,光线以任意角度入射,都会从AC面射出.但是在不同条件下,光线经三棱镜后,出射光线的传播方向可能偏向底面BC,也可能偏向顶角A,偏转方向的临界条件可以通过三棱镜中DE光线恰好垂直入射到AC面上所对应的入射角来判断,此时入射角i1满足
sini1=nsinA
而当入射角i1>arcsin(nsinA)时,折射光线DE将从E点入射到AC面,且出现在AC面的法线(过E点)的上方(如图2所示),那么,出射光线将向顶角A偏折.
图3给出了不同折射率的三棱镜的最小入射角随着顶角的变化关系,从图中可以看出最小入射角i1min随着三棱镜顶角A的增大而增大,图中直线PM表示三棱镜顶角A增大到极大值Amax后,对应的最小入射角都为90°,当三棱镜的顶角取PM直线上的值时,无论光线的入射角取何值,折射光在棱镜内的AC面均会发生全反射,无出射光线产生.每条曲线与横坐标的交点对应着顶角A的极小值Amin.
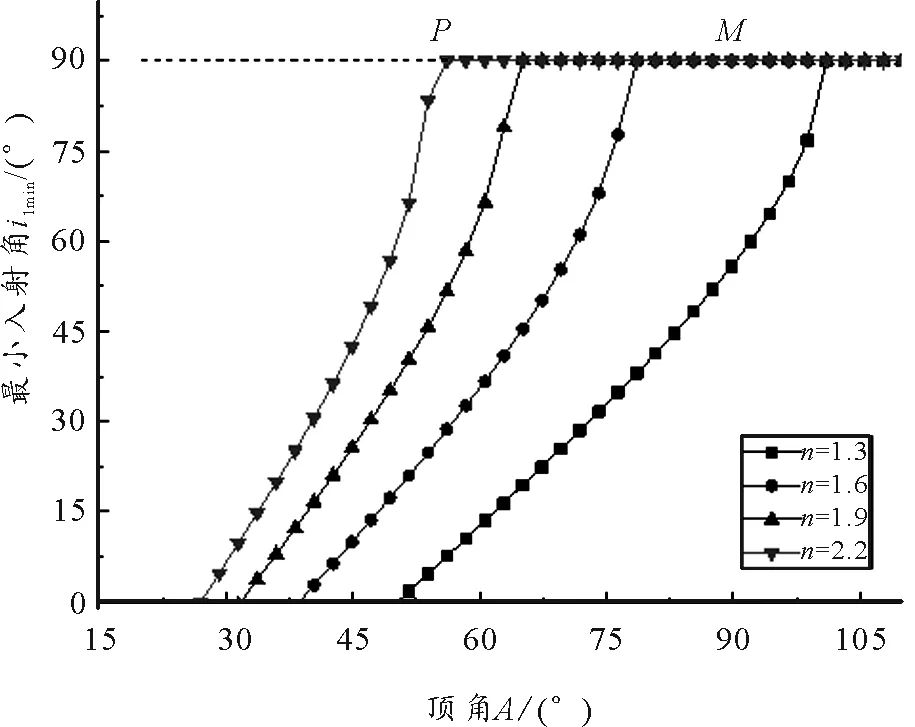
图3 不同折射率n下i1min-A关系
此外,顶角A的这两个临界值,也可以用代数求解的方法得到,设Amin,Amax分别对应最小入射角等于零和90°的情况,分别将i1min=0和i1min=90°代入式(4),有
(5)
(6)
解式(5)、(6)也可得
这与上面的分析是一致的.综上,在三棱镜的折射率n不变时,顶角A对出射光线的影响有以下规律.
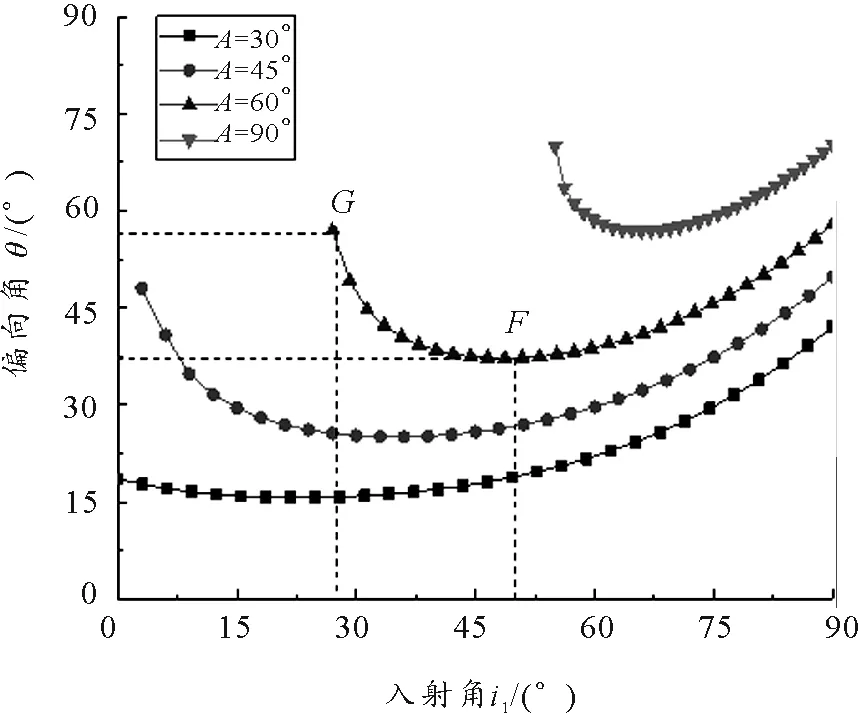
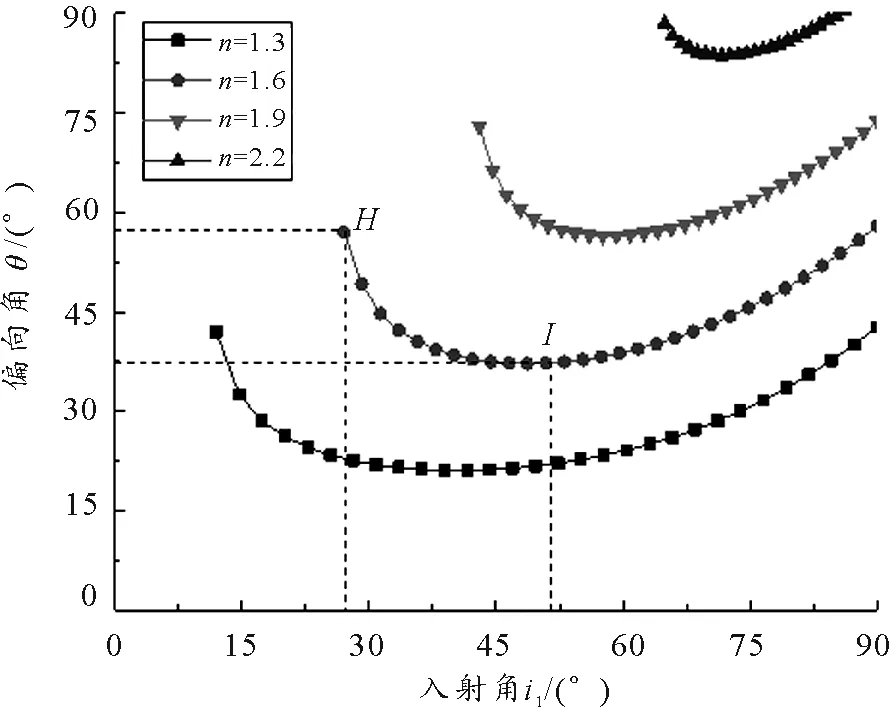
(1)当顶角A i1>arcsin(nsinA) 出射光线的传播方向将偏向顶角A(往AC面过E点的法线上方偏折),当i1 (2)当Amin (3)当A>Amax时,从AB面以任意角度入射的光线,进入三棱镜后,均会在棱镜内AC面上发生全发射,因此,不会有光线从AC面射出. 同理,当三棱镜的顶角A不变时,折射率n也会对最小入射角产生影响.由式(4)知,当折射率n增大时,i1min也随之增大,当n增大到某个值n′时,i1min增大到90°,这时由折射定律和几何关系可求得折射率的极大值 而折射率n值越小,对应的i1min也越小,当n减小到某值n″时,i1min可能减小到零,此时对应折射率的极小值 图4是具有不同顶角A的三棱镜的最小入射角i1min随折射率n的变化关系曲线. 图4 不同顶角A下i1min-n关系 从图4可以看出最小入射角随着折射率的增大而增大.图中线段QN表示折射率n取值达到某值n′后,AB面上任意角度入射的光线均在AC面上发生全反射.曲线与横坐标的交点表示折射率n的极小值n″,当n小于该值时,AB面上任意角度入射的光线均能从AC面射出.同样的,在这种情况下存在出射光线向AC面法线上方偏折的情况,其临界条件可以由DE光线恰好垂直入射到AC面时所对应的入射角来决定,即 i1=arcsin(nsinA) 当三棱镜顶角A不变时,折射率n对出射光线的影响规律可总结如下. 根据图1和图2,由几何关系可得三棱镜AC面出射光线与AB面入射光线之间的偏向角θ之间的关系为 θ=i1±r2-A (7) 其中加号表示出射光线经AC面向法线下方偏折,减号表示出射光线经AC面向法线上方偏折.结合折射定律可进一步算得偏向角与入射角i1、折射率n、顶角A的关系为 cosAsini1]-A (8) 从上式可以看出当三棱镜的参数n和A一定时,偏向角随着入射角的变化而变化. 图5是棱镜折射率n=1.5时,取不同的顶角A值,偏向角θ与入射角i1的关系曲线,图6是棱镜顶角为A=60°时,取不同的折射率n值,偏向角θ与入射角i1的关系曲线,θ-i1关系曲线上的点代表有出射光线时偏向角和入射角的对应关系. 图5 n=1.5时不同A对应的θ-i1关系曲线 图6 A=60°时不同n对应的θ-i1的关系曲线 从图5和图6可以看出,当棱镜折射率和顶角一定时,偏向角随着入射角的增大呈现先减小后增大的趋势.图中每条曲线最左端处对应的横坐标值为棱镜AC面有光线出射时需满足的最小入射角i1min值.图5中参数n=1.5,A=30°对应的曲线覆盖入射角全区段,这表示当光以任意角度入射到以该参数制作的三棱镜上时,光线均能从AC面射出,不会发生全反射.图5和图6中的θ-i1关系曲线可以看出,偏向角存在一个最小值θmin,在图5中当三棱镜的顶角A增加,出现最小偏向角所对应的入射角也随之增加.在图6中,三棱镜顶角A一定的情况下,棱镜的折射率越大,出现最小偏向角时对应的光线入射角也会随之增加.可计算出最小偏向角与三棱镜参数之间有如下关系 (9) 以参数n=1.5,A=60°的三棱镜为例,代入式(4)和式(9)中,得到最小入射角和最小偏向角分别为i1min=27.9°和θmin=37.2°.此外,如果知道θ-i1关系曲线图,也可以直接从θ-i1关系曲线中确定最小入射角和最小偏向角的大小,曲线左端点处的横坐标代表最小入射角的值,曲线最低点处的纵坐标值即为最小偏向角的值.如图5中G和F两点分别代表n=1.5,A=60°时的θ-i1关系曲线上的左端点和最低点,通过定位可确定两点的坐标分别为:G(27.5,56.5),F(50.1,37.5),表示当棱镜参数取n=1.5,A=60°时,对应的最小入射角为27.5°、最小偏向角为37.5°.同样,在图6中当棱镜参数取n=1.5,A=60°时曲线所对应的最小入射角和最小偏向角(即H,I两点),得到i1min=27.2°,θmin=37.4°,可见在误差允许范围内通过曲线关系图确定最小入射角和最小偏向角与公式得出的结果非常接近. 本文分析了光束通过三棱镜的偏折情况,讨论了入射角、折射率、棱镜顶角对出射光线偏折方向的影响,指出三棱镜的折射率、顶角存在着极小值和极大值的取值范围,当棱镜折射率或顶角小于其极小值时,以任意角度入射的光线都能从三棱镜另一侧面射出;当折射率或顶角的取值处在极小值和极大值范围之间,光线的入射角大于最小入射角时,才能在棱镜另一侧面得到出射光线,且最小入射角随着棱镜折射率和顶角的增大而增大;当折射率或顶角大于其极大值时,以任意角度入射的光线均发生全反射而不会有出射光线产生.此外,讨论了光线偏向角与三棱镜参数的关系,光线偏向角随着入射角的增大呈现先减小后增大的变化规律,且最小偏向角随着棱镜折射率和顶角的增大而增大.本文的分析和讨论有利于学生深入了解三棱镜对光线的转向情况,也能为三棱镜的设计提供参考.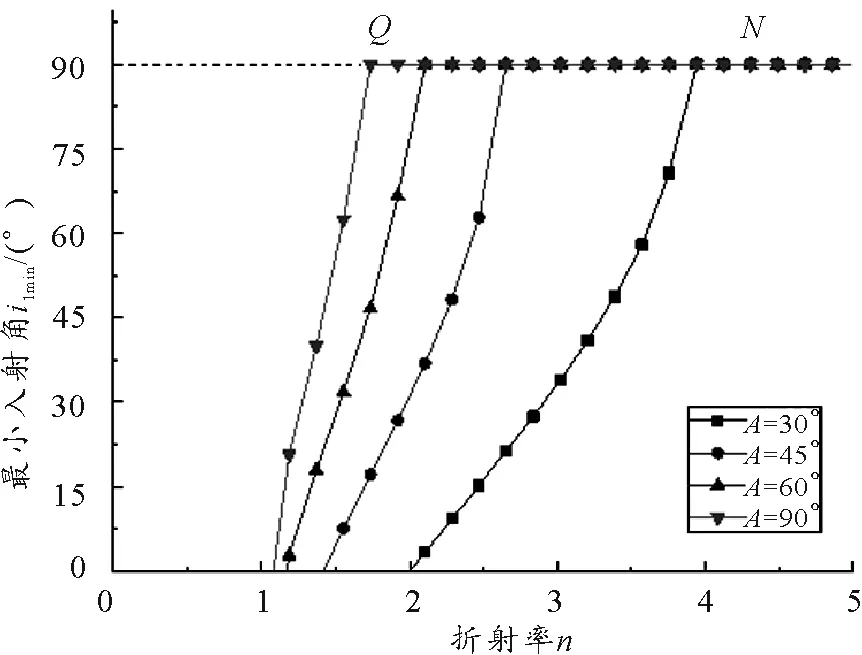
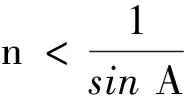

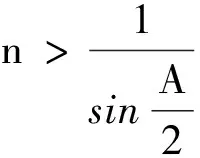
3 不同参数下偏向角随入射角的变化情况

4 总结
