1 000 kV苏通大跨越输电塔线体系气动弹性模型设计与分析

赵 爽， 晏致涛,2， 李正良， 董建尧， 聂小春

(1.重庆大学 土木工程学院，重庆 400044；2.重庆科技学院 建筑工程学院，重庆 401331；3.华东电力设计院有限公司，上海 200001)

拟建的苏通大跨越输电塔线路(下文简称苏通大跨越)是迄今为止世界上塔身最高、跨度最长的输电线路。风荷载作用下，由于导线与输电塔的耦合运动、流体与运动结构的耦合、三维气动力之间的耦合，大跨越输电塔线体系成为相当复杂的耦联柔性体系。气动弹性模型风洞试验是深入研究各种风致耦合振动现象的有效手段。

Bayar[1]制作刚性模型，模拟格构式输电塔外形，通过风洞试验研究密实度、风向角、风攻角等参数对阻力系数的影响，提出了阻力系数的计算公式，然而刚性模型测定的属于静态风效应。输电线风洞试验的研究，早期是通过节段模型获取阻力系数，然而模型风洞试验的结果通常要比实测结果大得多。Ball等[2]认为模型比例和边界条件会引起这种差异，但是主要原因却没有发现。由于风洞实验室的限制，Wardlaw等[3]采用小比例设计方案制作全跨输电线的气动弹性模型，通过风洞试验研究其动力行为。然而，与桥梁的缆索不同，输电线单位长度的质量和刚度均很小，从而过小的相似比使其气动弹性模型在结构基本缩尺律和构件层面的缩尺律等方面都存在一些问题。由于输电线气动弹性模型设计的困难，楼文娟[4]按照相似准则设计全塔气动弹性模型，通过风洞试验获得了风振响应和风振系数，研究结果未考虑输电线影响。Loredo-Souza等[5]提出一种变比例的输电线模型设计方案，采用该方案，可以进一步缩小输电线模型的跨度，从而有效地解决了输电线气动弹性模型设计难题。在此基础上，诸多学者进行了塔线体系气动弹性模型的风洞试验。梁枢果[6]以500 kV的某高压输电线路为背景，除了采用变比例输电线模型方案，其它缩尺率均满足相似准则，从而设计出精细的塔线体系气动弹性模型，研究了塔线耦联对输电塔风振响应的影响。同时，在大跨越输电塔线体系的风洞试验研究上也取得了进展。李正良[7]以1 000 kV汉江大跨越特高压输电线路为工程背景，对主跨1 650 m，塔高181.8 m的塔线体系，通过放松输电塔的Froude数相似准则进行了气动弹性模型风洞试验研究。邓洪洲等[8-10]以500 kV江阴大跨越高压输电线路为工程背景，对主跨2 300 m，塔高346.5 m，构件为角钢组合断面的塔线体系，通过气动弹性模型的风洞试验研究了塔线体系的风致响应和风振控制。郭勇等[11-14]以500 kV舟山大跨越高压输电线路为工程背景，对主跨2 750 m，塔高370 m的塔线体系，通过放松输电塔的Froude数相似准则进行气动弹性模型的风洞试验并结合时域和频域分析，研究了塔线体系的风致响应和风振控制。

以往的研究为输电塔线体系风洞试验的气动弹性模型设计提供了参考。对于塔高和跨度小的塔线体系而言，已经有了成熟的气动弹性模型设计方案，对于苏通大跨越，目前还存在以下问题没有解决。为了模型制作的可行，需要放松苏通大跨越输电塔模型的Froude数相似准则，基于同一风速原则，输电线模型将不满足Strouhal数相似准则，进而气动阻尼不满足理论相似比；由于输电线垂跨比大，采用传统的变比例输电线模型设计会导致模型的气动阻力与理论值的误差大于5%；塔身主材采用钢管混凝土材料，高风速下混凝土会因为受拉失效，从而影响实验结果的准确性；风洞实验室难以模拟梯度风高度以上的风剖面，需要对风洞试验结果进行处理，考虑梯度风高度的影响。本文通过刚性模型的风洞试验获取输电塔的气动力参数，进一步采用有限元模型分析输电塔放松Froude数相似准则和采用传统变比例输电线模型对输电塔位移、绝缘子内力、绝缘子风偏角和输电线位移的影响。通过增大输电线弹性刚度和采用公式推导出的精确变比例输电线模型，设计塔线体系气动弹性模型。在此基础上通过有限元模型分析梯度风高度和钢管混凝土的材料非线性对输电塔位移、绝缘子内力、绝缘子风偏角和输电线位移的影响。通过本文的研究，为此类塔线体系的气动弹性模型设计提供参考，并保证进一步的气动弹性模型风洞试验结果具有参考价值。

1 工程简介

苏通大跨越，属于淮南-南京-上海(北环)走向的1 000 kV双回路交流输变电线路试验示范工程的关键跨越。采用耐张塔-直线塔-直线塔-耐张塔布置，整个耐张段约5 km，导线与地线的跨度和垂度，如表1所示。采用6分裂导线，间隔棒间距45 m，导线物理参数，如表2所示。地线物理参数，如表3所示。直线塔高455 m，采用钢管混凝土的结构方案，混凝土灌到360 m高度处，耐张塔高112 m，主跨2 600 m。设计风速40 m/s，按B类地貌考虑。苏通大跨越示意图，如图1所示。

(a)输电塔(m)

(b) 塔线体系(m)

Tab.1 The span and sag of conductors andground wires (m)

类别边跨中间跨边跨档距111326001344地线垂度42.5231.563.4导线垂度45245.967.1

表2 JLHA1/G6A-500/400钢芯铝绞线物理参数

Tab.2 Physical parameters of JLHA1/G6A-500/400 ACSR

截面积/mm2保证拉断力/kN单位长度质量/(kg·km-1)外径/mm903.73860.224567.4139.14

表3 OPGW-350T物理参数

2 刚性模型气动力

在进行气动弹性模型设计之前，应该先进行刚性模型的气动力测试。刚性模型按照1/120的几何相似比设计[15]。输电塔构件为圆形截面，需要考虑Reynolds数影响，本文通过对原型节段的数值模拟和与之对应的节段模型风洞试验分别获得彼此的Reynolds数，根据Reynolds数与阻力系数的曲线图[16]，通过对模型迎风直径的修正来考虑Reynolds影响。采用不锈钢管制作输电塔刚性模型，通过增加钢管厚度保证其刚度。制作好的刚性模型，见图2。刚性模型采用五分量应变天平测量气动力，采样时间10 s，采样频率800 Hz，试验风速11.11 m/s，来流风向垂直于线路走向。通过刚性模型确定输电塔各段的气动力参数，阻力系数的分布，见图3。

图2 刚性模型

图3 阻力系数分布

3 气动弹性模型设计

气动弹性模型难以满足所有相似准则，根据研究目的，可以放松部分相似准则。采用谐波合成法[17-18]模拟风场。经对比，模拟风场与预期值吻合度好。输入刚性模型风洞试验确定的气动力参数，通过有限元模型计算塔线体系的塔身顺风向位移、上横担悬挂绝缘子内力、上横担悬挂绝缘子风偏角和上横担悬挂导线的跨中顺风向位移。计算数据均还原到原型结构。

3.1 放松输电塔Froude数的塔线体系模型设计

输电塔杆件以轴力为主，按二元杆考虑，通过Strouhal数相似准则和Cauchy数相似准则，杆件横截面积的相似比SA与频率相似比Sf的关系表达式为

(1)

式中:SE为弹性模量的相似比，Sg为几何相似比。

苏通大跨越输电塔杆件规格多，严格按照相似准则设计时，由于模型杆件横截面积很小，不能找到合适材料制作模型骨架。为了解决这个问题，可以通过放松输电塔模型的Froude数相似准则来增大模型杆件的横截面积。这样，根据Strouhal数相似准则，风速相似比Sv=SfSg。

输电线的结构阻尼小，强风下以气动阻尼为主，输电线模型第i阶模态的气动阻尼比[5]表达式为

(2)

(3)

考虑风洞实验室的最大截面尺寸(22.5 m×4.5 m)后，取Sg=1/120。模型骨架选用毛细不锈钢材料，SE=1/1。由模型材料规格确定SA=16.4182/1204，进一步根据公式得到Sf=16.418/1。满足几何相似、Strouhal数相似准则(输电线不满足)、Cauchy数相似准则、Reynolds数相似准则、Froude数相似准则(输电塔不满足)和惯性参数(输电线不满足)后确定的相似比，如表4所示。当放松输电塔Froude数相似准则，基于同一风速相似原则，表4中的相似比存在2个问题：①输电塔模型和输电线模型的频率相似比不一致，输电线模型将不满足Strouhal数相似准则，进而阻力相似比小于理论值1。这会导致输电塔位移的动力响应偏小，绝缘子内力和风偏角以及输电线位移的动力响应偏大；②输电线模型的质量相似比大于理论值1/1203，由于输电线在风荷载下为准静态响应[20]，质量在一定范围内变化影响不大。输电线的刚度矩阵由重力刚度、弹性刚度和几何刚度构成，本项目通过改变输电线模型的弹性刚度对模型进行修正。

通过对比5种模型工况，研究输电线改变弹性刚度对风致响应的影响。工况1为输电塔放松Froude数的塔线体系模型，工况2～5为输电塔放松Froude数后，输电线刚度分别为1.5倍～3倍(间隔0.5倍)的塔线体系模型。与原型结构对比，各工况的塔身位移、绝缘子内力、绝缘子风偏角和导线位移的相对误差，分别见图4、表5、表6和表7。图4(a)表明，放松输电塔Froude数相似准则和改变输电线弹性刚度对塔身位移平均值影响小。图4(b)中，放松输电塔Froude数相似准则后，塔身位移均方根值比理论值偏小，其相对误差由下到上逐渐减小。这是由于输电塔与输电线的频率不一致，输电线气动阻力变小时，塔线耦合下输电塔的动力响应反而变小。增大输电线弹性刚度，位移均方根值增大，与理论值比较，其相对误差由下到上逐渐增大。输电线弹性刚度为1.5倍～3倍(间隔0.5倍)时，均方根位移绝对值最大的相对误差分别为8.34%、5.81%、4.76%、3.83%和3.60%。

(a)平均值

(b)均方根值

表5中，放松输电塔Froude数相似准则对绝缘子内力平均值影响小，增大输电线模型刚度，绝缘子内力平均值增大，并且相对误差均小于5%。表6和表7中，输电塔放松Froude数相似准则对绝缘子风偏角和输电线位移的平均值影响小，增大输电线模型刚度，两者的平均值减小，并且相对误差均小于5%。表5～表7表明，放松输电塔Froude数相似准则，绝缘子内力和风偏角以及输电线位移的均方根值均增大，相对误差大于5%，但增大输电线模型刚度后响应的均方根值减小。以上分析表明，在一定范围内增大输电线模型刚度对放松输电塔Froude数相似准则的塔线体系模型具有修正作用。

表4 放松输电塔Froude数相似的塔线体系相似比

表5 改变输电线弹性刚度对绝缘子内力影响(%)

表6 改变输电线弹性刚度对绝缘子风偏角影响(%)

表7 改变输电线弹性刚度对输电线位移影响(%)

3.2 采用变比例输电线模型的塔线体系模型设计

多跨塔线体系，跨度通常是塔高的十几倍甚至几十倍，在风洞试验中需要跨度相似比的进一步缩小。变比例输电线模型是将几何相似比乘以变比例系数γ得到模型的跨度相似比。输电线要满足变比例前后质量、阻力和频率一致的原则[5]。在已知跨度和垂度时，通过积分得到两端等高的悬链线线长表达式为

(4)

(5)

式中：s为垂度。质量一致的表达式为

(6)

(7)

表8 采用变比例输电线模型的塔线体系相似比

分别对Davenport提出的变比例输电线模型(简称变比例1)和本文提出的精确变比例输电线模型(简称变比例2)采用有限元分析，对比其结构的风致响应与理论值的相对误差。其中，塔身位移、绝缘子内力和绝缘子风偏角的相对误差，分别见图5、表9和表10。图5中，变比例1的位移平均值和均方根值比理论值偏大，变比例2的和理论值的吻合度好。变比例1和变比例2的平均位移的绝对值最大的相对误差分别为5.58%和1.94%，均方根位移的绝对值最大的相对误差分别为6.48%和3.17%。表9和表10中，变比例1的绝缘子内力和风偏角的平均值、均方根值比理论值偏大。由于直线塔和耐张塔的输电线挂点有高差，采用两边等高的线长公式时，变比例2的绝缘子内力和风偏角的平均值、均方根值同样比理论值偏大，但是其相对误差在5%以内，与理论值吻合度好。以上分析表明，采用变比例2的设计方案更合理。

(a)平均值

(b)均方根值

类别变比例1变比例2平均值相对误差7.212.28均方根值相对误差13.021.83

表10 变比例输电线模型对绝缘子风偏角影响(%)

3.3 苏通大跨越塔线体系模型设计

通过增大输电线的刚度和采用本文提出的精确变比例输电线模型设计苏通大跨越塔线体系的气动弹性模型。输电线模型采用碳素线制作，直径按设计的迎风外径取值，免除包裹“外衣”的处理过程，由此确定输电线模型的弹性刚度将增大2.161倍。采用γ=0.5的精确变比例输电线模型方案，与刚性模型设计一样，气动弹性模型通过改变迎风外径来满足Reynolds数相似准则，塔身修正系数μ不为定值，与位置有关，输电线的修正系数μ=0.917。设计模型相似比，见表11。

采用有限元分析，对比本文设计模型和未修正模型(不改变输电线弹性刚度和采用传统变比例输电线模型)的风致响应与理论值的相对误差。塔身位移、绝缘子内力、绝缘子风偏角和导线位移的相对误差，分别见图6、表12、表13和表14。无修正模型和本文设计模型塔身的平均位移的绝对值最大的相对误差分别为5.08%和2.94%，均方根位移的绝对值最大的相对误差分别为6.90%和3.57%。就绝缘子内力、绝缘子风偏角和导线位移而言，无修正模型的均方根值的相对误差大于5%，而设计模型的平均值和均方根值的相对误差均小于5%。结果表明，苏通大跨越设计模型与理论值吻合度好。

(a)平均值

(b)均方根值

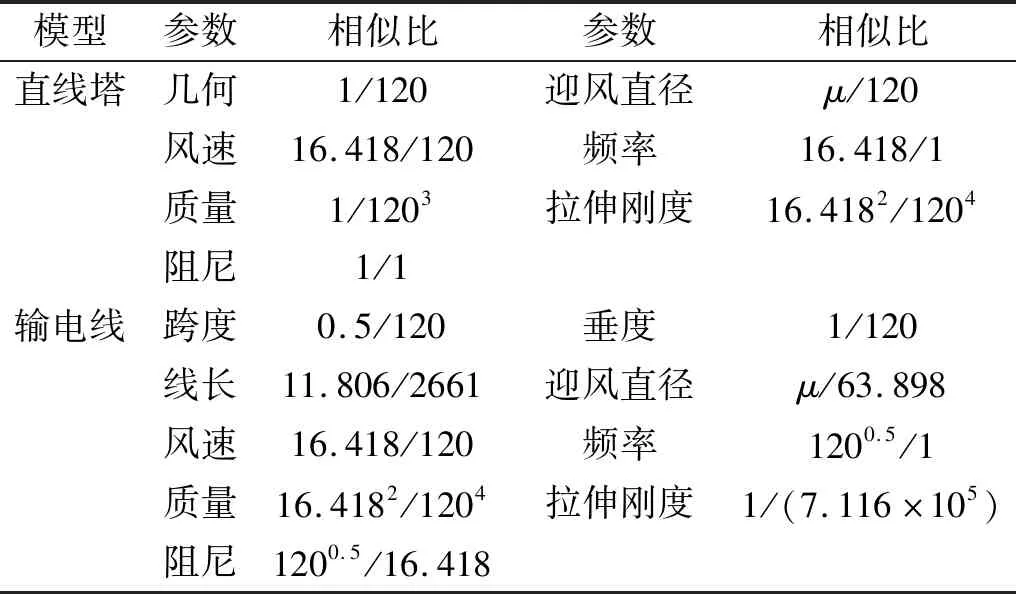
模型参数相似比参数相似比直线塔几何1/120迎风直径μ/120风速16.418/120频率16.418/1质量1/1203拉伸刚度16.4182/1204阻尼1/1输电线跨度0.5/120垂度1/120线长11.806/2661迎风直径μ/63.898风速16.418/120频率1200.5/1质量16.4182/1204拉伸刚度1/(7.116×105)阻尼1200.5/16.418

表12 不同设计模型的绝缘子内力误差(%)

Tab.12 Internal force error of insulator in different design models(%)

类别无修正模型设计模型平均值相对误差7.522.16均方根值相对误差19.014.00

表13 不同设计模型的风偏角误差(%)

Tab.13 Windage yaw angle error of insulatorin different design models(%)

类别无修正模型设计模型平均值相对误差3.350.93均方根值相对误差11.460.07

表14 不同设计模型的输电线位移误差(%)

Tab.14 Transmission line displacement error ofinsulator in different design models(%)

类别无修正模型设计模型平均值相对误差-1.63-4.39均方根值相对误差7.72-2.36

4 其他影响因素分析

4.1 材料非线性

由于模型构件的尺寸小，难以制作复合材料模拟钢管混凝土，并且气动弹性模型的相似准则适用于线弹性结构。通过有限元软件建模对比分析是否考虑钢管混凝土材料非线性对输电塔风致响应的影响。分析表明，在设计风速下，部分试验工况的部分钢管混凝土会因受拉而退出工作，但是与设计模型的风致响应对比，考虑钢管混凝土拉压的非线性本构后风致响应的最大相对误差为3.858%，影响小。因此，对于该模型设计，可以忽略混凝土因受拉而退出工作的影响，只需要采用改变钢材截面积来模拟钢管混凝土的抗压刚度，并保持外径和质量一致即可。

4.2 梯度风高度

风洞实验室不能准确模拟梯度风高度以上平流层，通过数值模拟B类地貌的理论风场，梯度风高度以上采用无湍流度的梯度风风速，并用有限元模型计算出考虑梯度风高度的风致响应。定义梯度风高度修正系数为考虑梯度风高度的风致响应值与不考虑梯度风高度的风致响应值的比值。风洞试验结果通过乘以梯度风高度修正系数来弥补风场模拟的不足。

设计风速下，塔身位移响应的梯度风高度修正系数沿高度分布如图7。不同风速下，测量响应平均值和均方根值的梯度风高度修正系数分别如图8和图9。将拟合公式附在相应的图中，其中，η表示梯度风高度修正系数；H为高度；v为平均风速；下标ut、uc、T、θ、mean、R.M.S分别表示输电塔位移、输电线位移、内力、风偏角、平均值、均方根值。图7中，输电塔位移的梯度风高度修正系数与高度呈线性关系，是否考虑梯度风高度对均方根位移的影响大，对平均位移的影响小，考虑梯度风高度后位移均变小。图8中，就响应平均值的梯度风高度修正系数而言，输电塔位移、绝缘子风偏角和输电线位移的与风速呈线性关系，然而绝缘子内力都与风速呈非线性关系，是否考虑梯度风高度对平均响应的影响小，考虑梯度风高度后响应的平均值均变小。图9中，就响应均方根值的梯度风高度修正系数而言，输电塔位移、绝缘子内力、绝缘子风偏角都与风速呈非线性关系，然而输电线位移都与风速呈线性关系，是否考虑梯度风高度对输电线位移均方根响应的影响小，对塔顶位移的影响大，考虑梯度风高度后响应的均方根值均变小。

图7 不同高度的塔身位移梯度风高度修正系数

图8 不同风速下平均响应的梯度风高度修正系数

图9 不同风速下均方根响应的梯度风高度修正系数

5 结 论

(1)当输电塔放松Froude数相似准则，基于同一风速相似原则，输电线气动阻力将会偏小。由于输电塔和输电线的频率不一致，输电塔位移的动力响应偏小，绝缘子内力和风偏角以及输电线位移的动力响应偏大。通过增大输电线的弹性刚度进行修正，苏通大跨越设计模型的风致响应与理论值吻合度好。

(2)当输电线的垂跨比大时，采用传统的变比例输电线模型，输电线模型的气动力偏大。通过公式推导确定精确变比例输电线模型的设计方案。塔线体系下，对比传统变比例输电线模型和精确变比例输电线模型的风致响应，结果表明前者与理论值的误差大，后者与理论值的吻合度好。

(3)通过增大输电线的弹性刚度和采用精确变比例输电线模型方案设计出苏通大跨越塔线体系气动弹性模型。对比无修正模型与设计模型的风致响应，结果表明前者与理论值的误差大，后者与理论值的吻合度好。

(4)通过有限元分析，设计风速下少数钢管混凝土构件中混凝土会因为受拉失效而退出工作，对输电塔风致位移的影响小。

(5)是否考虑梯度风高度，对平均响应影响小，对均方根响应影响大，对输电线位移的平均值和均方根值的影响小，对塔顶位移均方根值的影响大。塔身位移平均值和均方根值的梯度风高度修正系数与高度呈线性关系。塔身位移平均值、绝缘子风偏角平均值、输电线位移平均值和均方根值的梯度风高度修正系数与风速呈线性关系。其它响应的梯度风高度修正系数与风速呈非线性关系。