大型水陆两栖飞机舱段入水冲击实验研究
2019-07-08张家旭褚林塘
孙 丰, 魏 飞, 吴 彬, 张家旭, 褚林塘
(1. 高速水动力航空科技重点实验室,湖北 荆门 448035;2. 中国特种飞行器研究所,湖北 荆门 448035;3. 中航通用飞机有限责任公司,广东 珠海 519000)
近年来随着通用航空的迅猛发展,水上/水陆两栖飞机的价值不断得到体现,目前只有少数几个国家有能力研制大型水陆两栖飞机,国际上有代表性的水上/水陆两栖飞机机型有加拿大的CL-415、日本的US-2、俄罗斯的别-200以及美国的LAKE系列等,这些机型的性能体现了国外在相关领域的水平。国内从上个世纪70年代至今已成功研制了水轰5及鲲龙两型大型水上/水陆两栖飞机,鲲龙大型水陆两栖飞机的研制,对着水性能提出了更高要求,促进了着水冲击问题研究的开展。
水上/水陆两栖飞机在水面起降时,将产生复杂的流固耦合作用,在此过程中飞机要承受复杂的水动载荷,着水冲击载荷有着历程短、峰值高的特点,是水上/水陆两栖飞机结构设计及强度校核的主要载荷之一。水上/水陆两栖飞机船体横截面为楔形,国内外开展了大量楔形体入水撞击实验[1],用来分析着水载荷特性。Chuang[2]开展了一系列不同斜升角的楔形体入水实验,研究发现斜升角小于3°时,入水过程存在明显的气垫效应,变形体压力明显小于刚性体。Ochi等[3]根据船模试验数据分析,发现只有达到一定的相对速度,才能产生明显的砰击压力,给出了船底砰击压力估计的经验公式。Ei-Mahdi等[4]对不同斜升角的刚体模型压力试验结果进行了分析,给出了最大冲击压力估算公式。Aboulghit[5]开展了常速度楔形体和椎体刚性模型入水试验,分析了不同速度下的冲击力。Panciroli[6]、莫立新[7]及孙辉[8]等都对弹性楔形体入水试验进行了探索,分析了弹性变形对冲击载荷的影响。王明振[9]和褚林塘[10]选取水陆两栖飞机船体截面开展了入水冲击试验,研究了水陆两栖飞机着水载荷特性。
国内外关于入水冲击的理论及数值研究较多[11-12],这些研究成果急需试验的验证。一直以来关于水陆两栖飞机着水载荷的研究都以缩比刚性模型为主,不能考虑结构弹性变形对试验结果的影响,且缺乏缩尺比对载荷试验结果影响研究。通过水箱舱段着水载荷试验,测试着水过程水箱加速度、箱底压力分布,分析着水载荷特性,为水箱的结构设计和强度校核提供依据,同时为分析弹性变形及缩尺比对载荷的影响分析提供支持。
1 二维水动力冲击理论
水上飞机着水属于水动力冲击问题,可简化为楔形棱柱体与静水面撞击模型。水上飞机降落时砰击问题的理论研究是以经典的二元楔形体入水冲击理论为基础开展的,斜升角为β、单位长度质量为M的楔形体以初速度V0垂直落入水中,如图1所示,在任意下落深度为z处,c0为静水面处浸湿半宽,c为考虑水面隆起的实际浸湿半宽,ηb为考虑水面隆起的实际浸湿深度,应用动量守恒定理可得
MV0=(M+m)V
(1)
式中 :m为每单位长度的附加质量;V为任意下落深度处的垂向速度。

图1 楔形体入水冲击
对式(1)进行微分,可得冲击过程中任意瞬时作用于楔形体上的冲击力为
(2)
由式(2)可知,冲击力求解的关键取决于附加质量的准确度,Von-Karman及Wagner都使用平板拟合方法确定附加质量,如式(3),但浸湿半宽的形式不同,Von-Karman将浸湿半宽取为c0,Wagner取为c=πc0/2。
(3)
式中:ρ为水的密度。
1 试验设计
本试验件取自大型水陆两栖飞机机身中段水箱区域的结构,舱内安装有桁条、肋板、防晃板和隔板等构件,顶部和外端框安装有耳片接头,可用于试验过程中的起吊和悬挂。整个试验件长约1 600 mm,宽约3 200 mm,高约2 100 mm,空舱重量约为400 kg,底部斜升角30°。由于该试验件尺寸较大,配平、吊装、入水后的保护措施等问题都与以往同类试验有较大差异,通过在模型两侧对称位置布置配重袋,解决了模型配重及配平问题;通过有限元仿真分析确定了吊装点的强度,据此确定吊装方案;为了防止试验过程中模型倾覆,根据入水仿真预估模型入水深度,确定了保护绳的长度,保护绳既不会影响模型入水试验,又能起到保护作用。
图2为试验件吊装示意图,通过脱钩器与吊装钢索实现试验件与起吊装置的连接,保护绳用来防止模型入水后发生倾覆,试验中采用自由落体的方式,试验是在中国特种飞行器研究所的迫降水池中进行的,该水池主尺度为60 m×60 m×5 m。试验程序包含以下步骤:将试验模型配重到所需的重量状态,安装试验装置和试验件,检验传感器、采集系统、脱钩器等设备是否运行正常,调整试验件位于试验水域上方指定高度处,启动采集设备进行数据采集,遥控脱钩器脱钩,实现试验件入水,回收试验件,通过对比对称位置处的压力曲线判断模型是否垂直入水,分析数据的有效性。

图2 试验件吊装示意图

图3 传感器布置方案
试验采集参数包括:加速度(g)、压力(kPa),传感器的布置方案如图3所示,由于模型为弹性体,因此加速度应布置在刚度较大的位置,尽量避免测试数据出现过大的波动,图中所示的方框代表加速度传感器布置位置,圆圈代表压力传感器,共14个。其中P1-1、P3-1分别与P1、P3对称,用于验证模型是否对称入水。
试验包括3个重量状态,分别为空舱400 kg着水、配重至600 kg着水以及配重至1 200 kg着水,入水方式为自由落体着水,最大落水高度为2.5 m。表1为试验工况,表2为测试所需设备。
2 试验结果分析
图4为某工况下高速摄像系统拍摄的入水过程,图5为某工况下P1和P1-1位置处的压力时历曲线,由图可知,对称位置的压力曲线基本一致,由此判定模型入水过程的对称性。
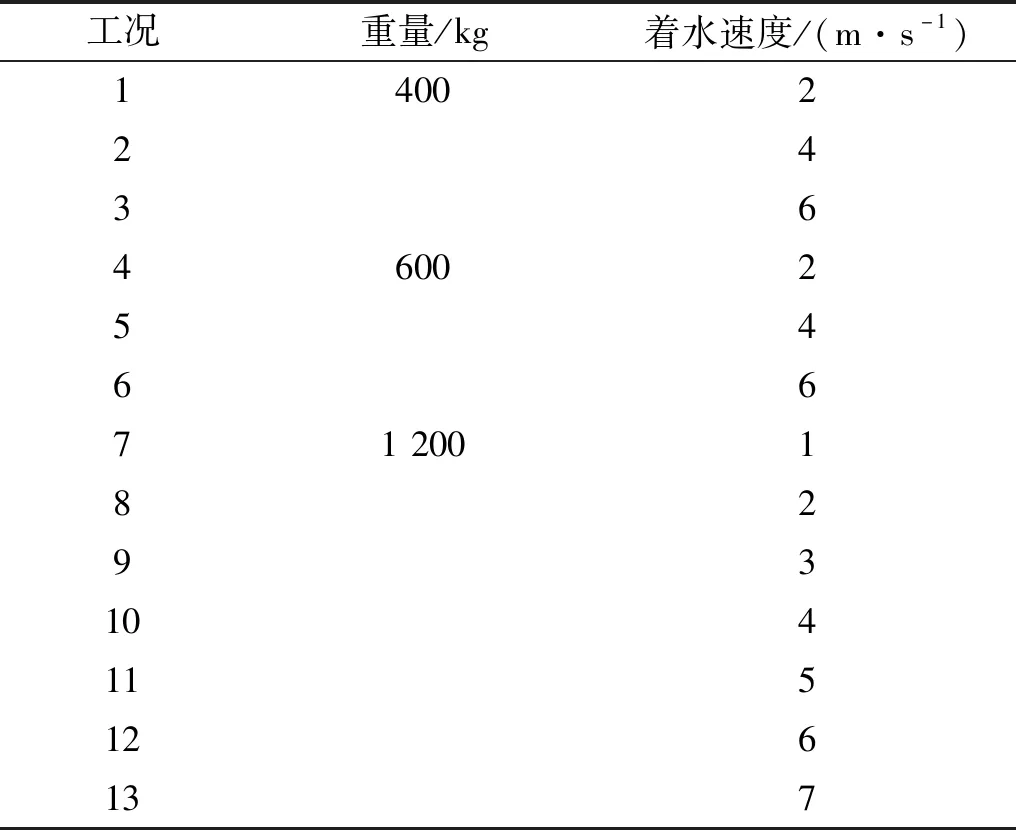
表1 试验工况

表2 测试设备

图4 入水过程

图5 对称位置压力
2.1 局部压力分析
选取工况6中横剖面处各测点压力时历曲线进行分析,如图6所示,由图可以看出,局部压力曲线呈现峰值大脉宽短的特点,随着测点距中纵剖面的距离的增大,压力传感器触水时刻越滞后,压力产生的时刻因此而延后,相邻两个测点的压力峰值时间间隔不断增大。从测点P5开始,压力曲线都出现了两个峰,通过分析试验录像可知这些测点的第一个压力峰应该由模型入水后产生的喷溅引起的,第二个压力峰是入水后的冲击产生的,两个压力的量值相当,文献[7]中同等规模的模型试验结果也出现了两次压力峰。
图7为舱段底部压力分布,图7(a)为工况4、5、6下各测点的压力峰值分布,可以看出,除个别测点外压力峰值大小基本沿着底面向上呈指数快速衰减,着水速度越大压力峰值越大,压力峰值分布衰减速度也越快;图7(b)为工况6下不同时刻各测点压力分布,图中11个时刻分别对应P1至P11压力测点峰值出现时刻,该工况下P12测点没有出现明显的冲击压力峰值,相同时刻,水面以下的各测点的压力随着水深的增加而逐渐减小,最大压力出现在自由液面附近,随着入水深度的增大,压力分布曲线形状逐渐变得平坦。
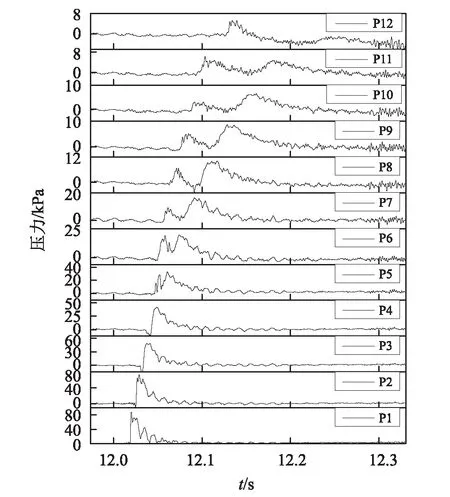
图6 局部压力时历曲线

(a)

(b)
2.2 加速度分析
图8为不同重量状态加速度峰值随入水速度变化曲线,由图可知,相同重量状态下,入水速度越大,加速度峰值越大,随着重量的增大,加速度峰值与入水速度关系的非线性越明显;相同速度下,重量越大,加速度峰值越小。

图8 加速度峰值随入水速度变化
公式(2)显示了冲击力是浸湿半宽的函数,无法给出时历的冲击力曲线,为了方便对比,将理论和试验的加速度结果整理为对应给定浸湿半宽的变化,将两种附加质量形式下的理论计算结果与试验结果进行对比,确定二者的适用性。图9为各重量状态在相同着水速度下加速度随浸湿半宽变化的试验结果,可知,重量越小,最大加速度对应的浸湿半宽越小,相同浸湿半宽处,入水前期,重量越大,加速度越小,入水后期,重量越大,加速度越大。

图9 不同重量下加速度随浸湿半宽的变化
选取3个有代表性的工况对不同着水速度下加速度随浸湿半宽的变化进行分析,图10~图12分别为工况9、11、13不同浸湿半宽下加速度的理论值与试验值,图中选取7个浸湿半宽点下的加速度进行分析,这7个点基本涵盖了模型从入水到最大浸深过程,总体看来速度对加速度随浸湿半宽的变化影响较小,Von-Karman理论与Wagner理论都与试验存在较大偏差,Von-Karman理论更接近试验结果,随着速度的增大,Wagner理论与试验结果的偏差越大,Wagner理论结果显示加速度峰值在较小浸湿半宽下产生,Wagner认为水面隆起增大了浸湿半宽,导致了附加质量被高估,这与骆寒冰等研究的中结论一致,造成理论与试验结果偏差大的原因主要包括:附加质量计算公式为近似估算,与实际存在偏差;入水冲击理论是基于刚体假设的基础建立的,而试验模型为弹性体;理论忽略结构所受的重力、浮力、水阻力等外力。图10中的试验结果曲线中加速度出现了负值,而理论结果却没有出现相同的现象,通过对所有工况的试验结果分析发现,着水速度小于3 m/s时都存在该现象,速度越小越明显,这主要是由于理论推导过程忽略的结构重量导致的,在重力的作用下,结构入水初期会有一个短暂的加速过程,着水速度越小,重力对结构入水过程影响越大,该加速过程越长,与理论的偏差也随之增大;模型重量越大,该现象也越明显,如表3所示。综上,Von-Karman理论适用于二元弹性体模型大速度着水时的定性分析。
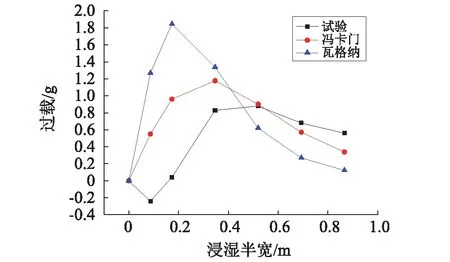
图10 3 m/s速度下加速度随浸湿半宽的变化

图11 5 m/s速度下加速度随浸湿半宽的变化
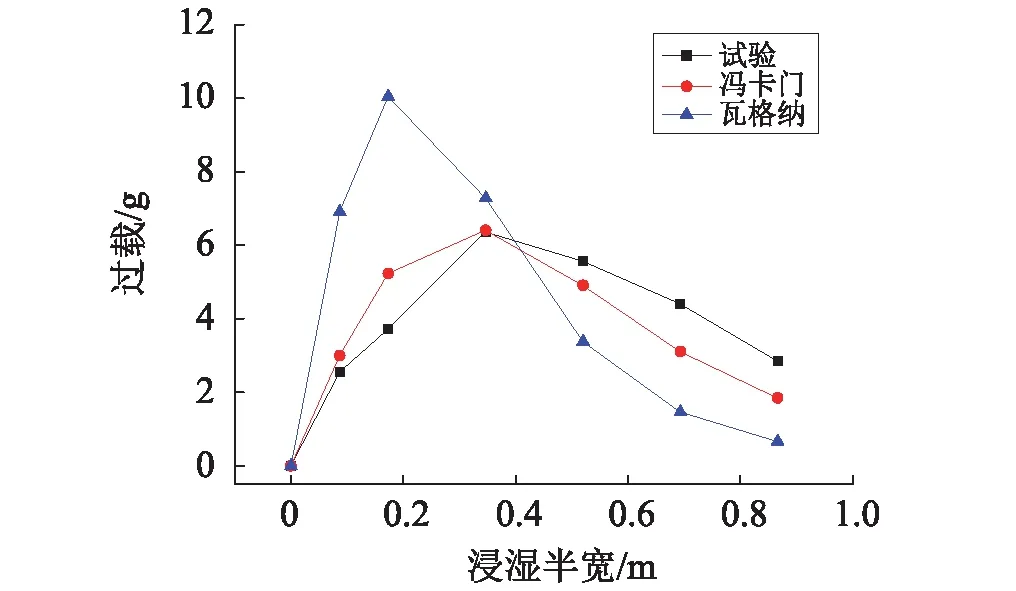
图12 7 m/s速度下加速度随浸湿半宽的变化

表3 相同浸湿半宽处各重量状态的负向加速度
3 结 论
针对大型水陆两栖飞机舱段在不同速度和重量状态下开展着水载荷试验,研究重量及着水速度对着水载荷的影响,并对比理论及试验结果,得到结论如下:
(1)局部压力曲线出现了二次峰值现象,两个压力的量值相当,在强度校核时应给予考虑;
(2)着水速度越大相同位置处压力峰值越大,横剖面上压力峰值分布衰减速度也越快;
(3)加速度峰值随着重量和入水速度的增大非线性增大;随着重量的增大,加速度峰值对应的浸湿半宽增大,速度对此影响较小;随着重量的增大,加速度与速度的关系的非线性越明显;
(4)Von-Karman理论较Wagner理论更接近试验结果,Wagner理论高估了附加质量,导致加速度峰值发生在较小的浸湿半宽;着水速度越小,模型重量越大,重力对结构入水过程影响越大,与理论的偏差也随之增大。
