落水洞直径对岩溶泉流量影响的试验研究

温忠辉+张依楠+苏佳林

摘要：基于裂隙-管道介质物理模型，通过设计多组试验方案，研究落水洞直径的改变对岩溶含水系统调蓄能力及泉流量过程的影响。经试验数据分析发现：调蓄系数随着落水洞直径增大而增大；在低强度下，落水洞直径的改变对裂隙和落水洞共同释水阶段的衰减能力影响不大，而在高强度下，其衰减能力随着落水洞直径的增大明显减小；底部管道释水阶段的衰减系数不受补给强度和落水洞直径的影响，其值约为0.0017 1/h ；调蓄系数与第一阶段衰减系数的乘积与落水洞直径无关，与补给强度呈负相关关系。

关键词：岩溶泉流量；物理试验；落水洞直径；调蓄系数；衰减系数

中图分类号：P641 文献标识码：A 文章编号：1672-1683（2017）04-0111-06

Abstract：Using the physical model of fissure-conduit media，we designed several experiments to study the effects of sinkhole diameter variations on the storage capacity and spring flow process of the karst aquifer system.Data analysis revealed that the regulating coefficient increased with the increase of sinkhole diameter.At low recharge rates，the variation of sinkhole diameter had little effect on the attenuation capacity at the stage where the fissure and sinkhole released water simultaneously.However，at high recharge rates，the attenuation capacity obviously declined with the increase of sinkhole diameter.The attenuation coefficient at the stage where the bottom pipeline released water was about 0.0017 1/h，and it was not affected by the recharge rate or the sinkhole diameter.The product of the regulating coefficient and the attenuation coefficient of the first stage was negatively correlated to the recharge rate，but was independent of the sinkhole diameter.

Key words：karst spring flow；physical experiment；sinkhole diameter；regulating coefficient；attenuation coefficient

1 研究背景

在我國西南岩溶地区，虽降水充沛，但由于该地区的落水洞、岩溶漏斗、地下河天窗等地表岩溶地貌极其发育，大气降水及地表水会沿着这些岩溶通道集中入渗补给地下水，从而导致地表水匮乏，人水矛盾突出[1]，并且水资源短缺问题将随着岩溶地貌进一步发育而更加严重。近年来，许多学者对西南岩溶地区含水系统水动力特征展开研究，以便为解决水资源问题提供有力的理论支撑。

落水洞作为岩溶垂直发育阶段的产物，是岩溶含水介质内主要的集水区域和过流通道[2]。其在形成的初始阶段，侵蚀作用以沿垂直裂隙的溶蚀为主。当孔洞扩大以后，补给强度很大时，大量地表水流集中汇入落水洞，水流所携带的大量泥沙石砾不断地对洞壁四周进行磨蚀，同时还会伴随着岩体的崩塌，使落水洞迅速扩大[3]。相比落水洞的扩大速度，岩溶裂隙和地下河因受地下水流的溶蚀所引起的尺寸改变可忽略。落水洞除起着汇水和输水作用外，在补给强度很大的情况下，落水洞内很可能来不及消水，水位壅高[4]，这时落水洞还起着储水作用。由此可见，落水洞对岩溶含水介质水流运动有着重要影响。

岩溶含水介质水流运动研究的一个重要方面是泉流量过程的研究，特别是泉流量衰减过程[5]。泉流量衰减过程不仅反映含水层的结构特征，亦反映含水介质对地下水的调蓄能力。黄敬熙[6]利用流量衰减方程计算各亚动态贮水量占总贮水量的百分比，分析了洛塔地区不同块段岩溶水的主要赋存形式。程星等[7]从影响岩溶地下水调蓄功能的因素出发，对影响岩溶泉流量衰减的岩性、构造、降水入渗方式、洞穴地貌演化阶段、排泄条件等因素进行了定性分析。孙晨等[8]利用裂隙-管道双重介质物理模型，定量分析了泉口大小、降雨、蓄水状态等对泉流量衰减过程的影响。

目前，针对落水洞对岩溶泉流量过程影响的研究还未多见。本文将以落水洞为研究对象，探究岩溶通道的发育程度对含水系统地下水流运动规律的影响。因实测资料有限，理想化数学模型适用范围受限制，所以依据西南岩溶地区的水文地质概念模型，建立了含有落水洞的裂隙-管道介质物理模型，通过改变落水洞直径来探讨其对岩溶含水系统调蓄能力及泉流量过程的影响，以期为岩溶地貌发育对地下水流运动规律影响的研究提供参考。

2 研究方法

2.1 物理模型

物理模型之所以成为研究岩溶含水系统的有效工具，是因为其在一定程度上可以按照野外实际的水文地质条件进行任意改变[9]。本文通过对裂隙-管道介质水文地质概念模型合理简化，建立了如图1中的裂隙-管道介质物理模型。该物理模型由三部分组成：裂隙-管道介质区、降雨补给系统、流量采集系统。裂隙-管道介质模拟区长1.20 m，高 0.89 m，宽0.04 m，其中水平层间裂隙隙宽为2 mm，共设8层；垂直裂隙隙宽为1 mm，每层10条。裂隙网络右侧和底部均设置一条截面为0.04 m×0.04 m的方形管道，其中右侧管道模拟落水洞，底部管道模拟地下暗河。降雨补给系统采用共同补给方式，即裂隙分散补给和落水洞集中补给，并通过调节阀门控制补给强度大小。流量采集系统与底部管道连通的泉口处接有电磁流量计，以便实时记录出口流量的变化过程。

3 试验过程与结果分析

3.1 试验过程

3.1.1 方案设计

准备2种不同尺寸的垫片，其中尺寸为85 cm×4 cm×0.5 cm的垫片4个，尺寸为85 cm×4 cm×0.25 cm的垫片1个。然后，将两种垫片进行随机组合，放入模型右侧的落水洞中，以改变落水洞的直径。落水洞直径从2 cm增加到4 cm，每增加0.25 cm为一组方案，共九组试验方案。

此外，由于泉流量过程与补给强度有关，为保证结果的合理性与可靠性，每组方案下设置多种不同补给强度。

3.1.2 操作过程

开启补给阀门，并保持补给强度不变，直至装置内水位不再变化时停止补给。当泉口停止排水时，即为一个完整的泉流量过程。此过程由电磁流流量计每隔一秒记录一次，数据可用U盘直接从温压补偿流量积算器设备中拷贝，节省人力与时间。

3.2 结果分析

3.2.1 泉流量过程

根据试验所得到的时间流量序列，绘制泉流量过程曲线，见图2。由图2可见，一个完整的泉流量过程分为三个阶段：上升阶段，平稳阶段和下降阶段。其中下降阶段又分为四个阶段，先陡然下降，再平缓下降，后急剧减小至零，最终以零流量持续至断流。其中，后两个阶段是当模型中水位降至泉口后的衰减过程，由于此阶段泉口不饱和，流量计无法准确测出其流量值。因此，在后面分析中不做考虑。不同补给强度及不同落水洞直径情况下，其泉流量过程曲线均与图2类似。

3.2.2 补给强度与稳定水位

补给强度与稳定水位存在着正相关关系，补给强度越大，稳定水位越高。本试验共有九种不同的落水洞直径方案，取落水洞直径为2 cm、2.5 cm、3 cm、3.5 cm和4 cm五种情况，将其不同补给强度下的稳定水位点绘在同一张图上，见图3。

由图3可见，这些散点大致分布在某一固定的直线上，经计算可确定这一直线方程为y=0.011 36 x+0.988 09。即在不同的落水洞直径下，补给强度与稳定水位之间的关系是确定的。

3.2.3 调蓄系数

选取各方案下泉流量过程的第一阶段，即泉流量上升阶段，采用式（2）计算不同直径的落水洞的调蓄系数，计算结果见表1，并绘图4。

由表1可见，同一直径下，补给强度越大，调蓄系数越小。由前面可知，补给强度越大，稳定水位越高，模型中蓄水量越大，但同时达到稳定水位所需要的时间也越长，因而，补给量在模型中滞留的比例越小，调蓄能力越弱。由图4可见，在同一补给强度下，调蓄系数随着落水洞直径的增大有增大的趋势。由前面可知，补给强度相等时，稳定水位也基本相等，落水洞直径越大，模型中蓄水量越大，同时达到稳定水位所需时间基本相等，因而，补给量在模型中滞留的比例越大，調蓄能力越强。

3.2.4 衰减系数

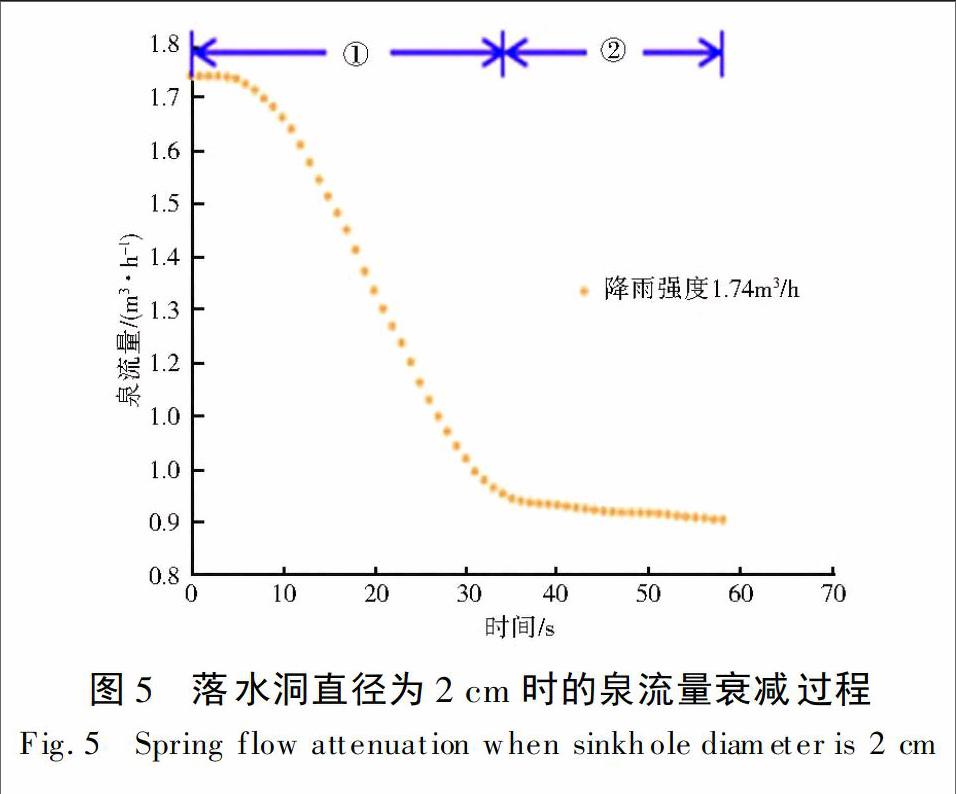
泉流量衰减过程仅考虑前两个阶段，即陡然下降阶段和平缓下降阶段，详见图5中的①和②。经数据分析可知，前者为裂隙和落水洞共同释水阶段，后者为底部管道部分释水阶段。采用式（3）分别对两个阶段进行曲线拟合，求出相应的衰减系数。

（1）第一阶段衰减系数。

裂隙和落水洞共同释水阶段的衰减系数与补给强度和落水洞直径的关系见图6和图7。由图6可见，衰减系数随着补给强度先增加后趋于不变，转折点在补给强度为1.5 m3/h左右。其它不同直径落水洞的第一阶段衰减系数变化趋势均与上述相同。由图7可见，在不同补给强度下，衰减系数均随着落水洞直径的增大而减小。其中在低强度下，落水洞直径的改变对衰减能力的影响不大，斜率小于0.001。而在中等强度和高强度下，衰减系数均随着落水洞直径的增大呈直线下降趋势。这是因为补给强度越高，稳定水位越高，不同直径落水洞的稳定蓄水量相差越大。

此外，利用式（4）计算第一阶段的衰减速率，取其中五种直径，点绘其衰减速率与补给强度的散点图。由图8可见，同一直径下，衰减速率随着补给强度的增加先增加后趋于平稳，转折点在补给强度为1.7 m3/h左右。在低强度下，不同直径落水洞下的衰减速率相差不大。高强度下，落水洞直径越大，其衰减速率越小。上述变化规律与衰减系数基本一致。

（2）第二阶段衰减系数。

底部管道释水阶段的衰减系数与补给强度和落水洞直径的关系见图9和图10。由图9可知，衰减系数随着补给强度变化不大，因此，可求其均值作为不同直径落水洞下的衰减系数。由图10可知，落水洞直径的改变对底部管道释水能力的影响不大。经计算，第二阶段的衰减系数大约为0.001 7 1/h ，数量级为-2，比第一阶段小一个数量级。平均衰减时间为23 s，相当于模型蓄水一半时第一阶段的衰减历时。

由表2可见，B值范围在0.007～0.012。在同一补给强度下，不同直径落水洞的B值相差不大，可认为B值与落水洞直径无关。在同一直径下，B值随着补给强度增大而减小。经计算，可确定B与i之间的关系为：B=-0.004 29i+0.016 24。

4 结论

本文通过设计多种试验方案，探讨了落水洞直径大小对岩溶含水系统调蓄能力及泉流量衰减过程的影响。主要得出以下结论。

（1） 调蓄能力与补给强度呈负相关关系，与落水洞直径呈正相关关系。

（2）裂隙和落水洞共同释水阶段的衰减系数随着补给强度先增加后趋于不变，存在转折点。在低强度下，落水洞直径的改变对衰减能力影响不大。而在高强度下，衰减能力随着落水洞直径的增大明显减小。

（3） 底部管道释水阶段的衰减系数不受补给强度和落水洞直径的影响，衰减系数大约为0.001 7 1/h ，比第一阶段小一个数量级。

（4） 调蓄系数与第一阶段衰减系数的乘积与落水洞直径无关，与补给强度呈负相关关系。