盐湖地区RC桥梁结构时变车桥耦合振动寿命预测研究

李双营， 赵建昌

(1. 兰州交通大学 土木工程学院，兰州 730070；2. 青海民族大学 建筑工程学院，西宁 810007)

钢筋锈蚀是影响RC桥梁结构耐久性和使用寿命的重要因素之一。一般情况下，铁路混凝土桥梁中钢筋腐蚀主要由于混凝土碳化至钢筋表面，而使钢筋表面的钝化膜赖以存在的碱性环境被破坏所致，也就是钢筋混凝土保护层被碳化。同样，在近海区域或盐湖地区，铁路混凝土桥梁中钢筋表面集聚较高浓度的氯离子，氯离子侵蚀是导致钢筋锈蚀的首要因素[1]，而盐湖地区氯离子对钢筋锈蚀程度要比近海区域环境更加严重和恶劣。我国的盐湖带主要分布于西北和内蒙境内，其盐湖面积约占国土面积的一半，盐湖含盐量非常高，尤其是青海、新疆、西藏和内蒙境内盐湖含盐量分别高达278.96 g/L、 340.51 g/L、 269.39 g/L和195.45 g/L，其中，对RC桥梁结构锈蚀的Cl离子浓度达到92.29～204.209 g/L[2]。由此可见，我国青藏铁路线桥梁和内蒙古境内铁路线桥梁大多处于Cl离子侵蚀环境下，这就使得盐湖地区氯离子侵蚀成为威胁RC桥梁结构健康的首要因素。

随着高速列车速度的不断提高，其高速运行时产生的垂向振动也逐渐增强。当列车通过桥梁时，在轨道不平顺激励下，桥梁在荷载的作用下发生强迫振动，从而产生车桥耦合振动，其振动频率随着列车速度的增加而逐渐增大，而当桥梁本体的振动频率和列车垂向振动频率相同时，产生共振现象。尤其是在盐湖地区的RC桥梁结构长期遭受氯离子锈蚀情况下，当列车高速通过桥梁时，一旦共振产生，则桥梁振幅较大，进而引起桥梁上部结构受力发生变化和桥梁振动加剧，可能导致桥梁混凝土开裂和钢筋断裂等危害，进而危及桥梁结构的安全。

在RC桥梁结构长期遭受氯离子锈蚀情况下，研究RC桥梁框架结构时变振动损伤问题具有非常重要的理论与工程意义，因此，许多专家和学者对Cl离子锈蚀情况下，RC桥梁结构安全性方面开展了大量理论和试验科研工作，其目的是研究运行于盐湖地区RC桥梁上高速列车的振动对桥梁结构状态的影响和损伤，并提出应对策略，并且也得到了大量的研究成果。但是，目前为止，这些研究方向和成果主要表现为两个方面，其一，盐湖地区氯离子对RC桥梁的锈蚀模型的建立，及其对桥梁结构的寿命预测。例如，确定了RC桥梁结构可靠度锈蚀模型[3]、提出了考虑荷载影响和氯离子结合能力的沿海在役钢筋混凝土桥梁的钢筋锈蚀模型[1]、氯离子锈蚀情况下混凝土结构耐久性及寿命预测研究[4-5]；其二，普通环境下(无氯离子锈蚀情况下)，车桥耦合振动影响因素和机理分析。例如，文献[6]从列车系统与桥梁之间能量传递、耦合系统的特征方程和反馈机制三个方面综合考虑，提出一种避免耦合振动的方法；文献[7]在轨道不平顺激励下，用统计线性化方法分析车桥非线性随机振动，取得良好的结果；虽然这些方法在确定车桥耦合振动模型时，既综合考虑了车辆、轨道、桥梁各部件相互作用力和车辆重力因素，也考虑了随机性的轨道不平顺激励，但是没有考虑列车运行速度对车桥耦合振动的影响。

综上所述，对于既考虑氯离子锈蚀又考虑列车运行速度情况时，RC桥梁整体结构振动特性的研究还未曾涉及。 因此，本文旨在对盐湖地区氯盐侵蚀环境下，列车以不同速度在桥梁上运行时，进行RC桥梁结构振动性能研究，得到列车以不同速度在RC桥梁上运行时的荷载影响因子f(δ)，从而构建既考虑氯离子结合能力又考虑基于列车运行速度的荷载影响因子f(δ)的盐湖地区RC桥梁结构使用寿命预测模型，实现对盐湖地区RC桥梁整体结构多龄期时变车桥耦合振动剩余使用寿命的预测。

1 盐湖地区RC桥梁结构使用年份预测

1.1 Cl离子诱发RC桥梁钢筋锈蚀的机理

由于盐湖地区RC桥梁长期与氯离子接触，因此，氯离子以扩散或毛细孔吸附的方式侵入到RC桥梁结构内部的钢筋表面，开始电化学反应，造成钢筋锈蚀。这种锈蚀是一个很复杂和产物多样性的电化学过程，因为其不但要满足阴、阳极反应条件外，还要具备传输通道、电子通道和热力学条件，当这几个条件满足后，钢筋锈蚀反应才能开始和持续发展[8]。锈蚀过程，如图1所示。

图1 氯离子锈蚀机理

由图可知，锈蚀过程如电池作用，锈蚀电池的电压为钢筋表面的电位差所产生，而锈蚀电池电极为阳极或阴极效果的钢筋不同表面所形成，因此，钢筋锈蚀过程构成电化学反应，反应过程如下。

(1)阳极反应

在阳极，铁失去电子变成铁离子，经过化学反应生成水溶性氯化铁(FeCl2·4H2O)，于是钢筋表面钝化膜被破坏。

Fe→Fe2++2e-

(1)

Fe2++2CI-+4H2O→FeCI·4H2O

(2)

(2)阴极反应

在阴极，水、氧和从阳极传输过来的电子发生化学反应，生成氢氧根离子，该反应并不造成钢筋的锈蚀，反而会起到保护作用。

O2+2H2O+4e-→4OH-

(3)

(3)生成物

水溶性氯化铁(FeCl2·4H2O)向含氧量较高的RC孔溶液中迁移，生成Fe(OH)2。根据环境条件，这些中间产物将继续进行反应，最终生成铁锈。

FeCI·4H2O→Fe(OH)2+2HCI+2H2O

(4)

4Fe(OH)2+O2+2H2O→4Fe(OH)3

(5)

通常情况下，盐湖地区氯离子通过扩散和毛细管吸附等方式进入并渗透RC桥梁保护层，到达钢筋表面，进而与钢筋钝化膜发生以上化学反应，最终导致钝化膜局部破坏而引起钢筋锈蚀。

1.2 RC桥梁Cl离子扩散模型

氯离子在RC中的扩散过程是一维扩散，其扩散过程符合Fick第二扩散定律[9-10]。基于Fick第二扩散定律的理论、质量守恒定律和实际工程经验总结，得到RC中氯离子扩散的控制方程

(6)

式中:C为氯离子质量分数，%；t为时间；x为距混凝土表面的距离；D为混凝土中氯离子扩散系数，m2/s，Cl离子扩散系数受RC质量与环境影响而具有时间相关性，Thomas等[11]提出了氯离子扩散系数随时间变化的表达式

(7)

式中:Dt为时间t时RC中氯离子扩散系数；D0为时间t0时RC中氯离子扩散系数；t为时间，a；m为模型参数。

实际工程中，RC桥梁上通常有列车运行，引入影响氯离子扩散的荷载影响因子f(δ)和考虑氯离子结合能力的参数R[12]。因此，得到考虑荷载影响因子及氯离子结合能力的RC桥梁氯离子扩散修正模型。

(8)

1.3 RC桥梁结构使用寿命修正计算模型

氯离子侵入混凝土引发钢筋锈蚀是导致盐湖地区RC桥梁结构破坏的最主要的也是最危险的原因。在1.2节基础上，本文根据吴庆令所提出的用于计算海工混凝土中钢筋开始锈蚀时间的寿命计算模型，将该模型中的相关参数进行修正，建立考虑f(δ)(包括列车运行速度)和氯离子结合能力的盐湖地区RC桥梁结构使用寿命数学模型，如式(9)所示。

(9)

式中:tcr表示剩余使用寿命(a)；K表示混凝土氯离子扩散性能的劣化效应系数；ccr表示临界氯离子浓度。

2 基于虚拟激励法的RC桥梁车桥垂向耦合振动分析

当列车通过桥梁时，在轨道不平顺激励下，桥梁在荷载的作用下发生强迫振动，因此，发生车桥耦合振动，这种振动既包括垂向振动也包括横向振动，其振动频率随着列车速度的增加而逐渐增大，加速度和位移也逐渐增强，因此，轨道不平顺是车桥耦合系统的主要激励。虚拟激励法的优点是将简谐振动分析用于平稳随机振动分析，将确定性时间历程分析应用于非平稳随机振动分析，从而精简计算过程，并能保持计算结果的精确[13]。由车辆动力学的研究表明[14]，车辆垂向与横向振动之间的耦合效应较弱，再基于本文分析车桥耦合振动目的主要是为了研究和得到氯离子对RC桥梁扩散渗透作用的主要影响因素荷载影响因子f(δ)，得到不同车速下荷载影响因子f(δ)的取值情况，而f(δ)的取值与列车垂向振动位移h及列车车体质量有关，与列车横向振动无关，因此，对车辆的横向振动暂未做研究。本文将轨道不平顺视为多点平稳随机激励，基于虚拟激励法研究不同车速下车桥时变耦合系统的垂向随机动力特性。

2.1 车辆垂向模型及运动方程

2.1.1 车辆垂向模型

铁路客车车辆一般由车体、2个转向架、4个轮对等主要部件组成，主要部件都简化为刚体。车体和转向架之间通过二系悬挂装置连结，转向架和轮对通过一系悬挂装置连接，悬挂装置主要由弹簧阻尼器组成，因此车辆为多自由度的振动系统。其中，车体和转向架分别有横移、沉浮、侧滚、摇头和点头5个自由度。在建模时，忽略车体、转向架、轮对的弹性变形和横向振动，因此仅考虑浮沉和点头2个自由度。车辆系统垂向模型，如图2所示。

图2中，zc和βc分别表示车体浮沉运动和点头运动；zt1和βt1分别表示前转向架浮沉运动和点头运动；zt2和βt2分别表示后转向架的浮沉运动和点头运动；zw1～zw2分别表示4个轮对的浮沉运动；lc是车辆定距的之半；lt是车辆轴距之半。

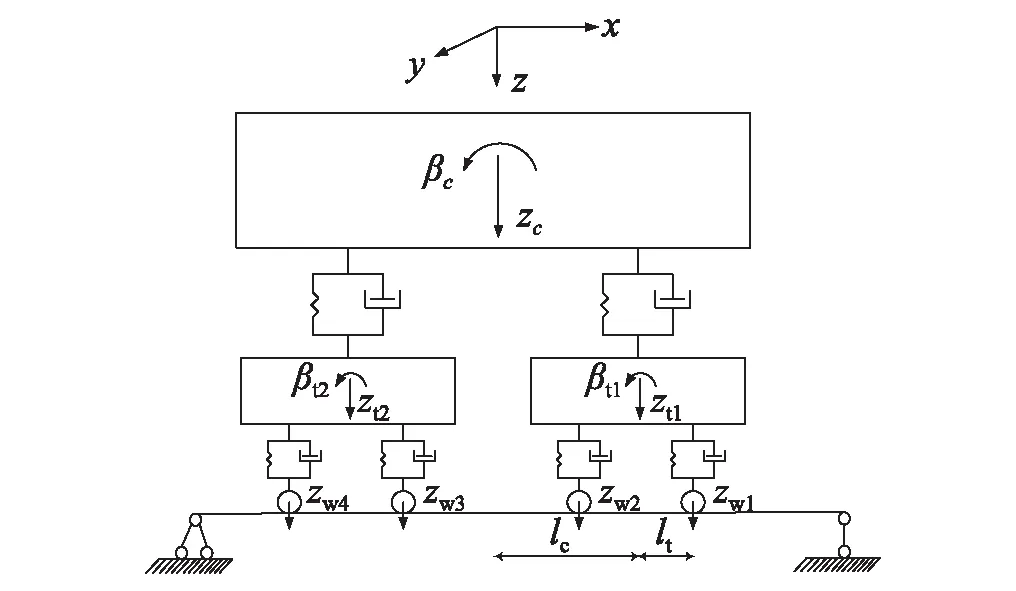
图2 车辆垂向模型

2.1.2 车辆运动方程

由车辆垂向模型图，建立矩阵形式的车辆系统运动方程，如式(10)所示。

(10)

2.2 桥梁系统运动方程

考虑实际RC桥梁结构的复杂性，本文采用有限元法建立桥梁模型，在建立RC桥梁模型时，RC桥梁各结构通过杆单元、梁单元、板壳单元等模拟。RC桥梁系统采用空间梁单元，每单元形成6个自由度，沿着x,y,z轴的平移和绕着3轴的转动，则RC桥梁系统的运动方程如式(11)所示。

(11)

2.3 车桥(垂向运动模型)时变耦合关系及虚拟荷载

2.3.1 车桥垂向模型耦合关系的建立

轮轨相互作用模型(轮轨接触关系)是车桥系统的关键问题，而垂向轮轨关系又是车桥系统垂向振动最主要研究问题，但是，计算轮轨之间垂向相互作用力的过程比较复杂，本文不再赘述。车桥耦合系统垂向随机振动分析模型，如图3所示。

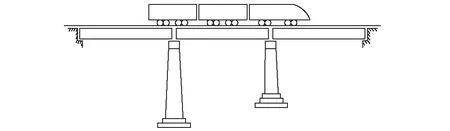
图3 车桥耦合系统垂向随机振动分析模型

同时，借鉴文献[15]的方法，可认为桥梁对车辆的垂向力直接作用于转向架，因此，得到车桥系统垂向运动模型，如式(12)所示。

(12)

2.3.2 车桥时变耦合系统的虚拟激励

车桥垂向耦合系统运动方程式(12)可写成

(13)

式中:F1(t)为车辆重力引起的确定性荷载项；F2(t)为轨道高低不平顺引起的不确定性随机荷载项。

在构造虚拟激励响应过程中，假设轨道高低不平顺为零均值平稳过程，则车桥耦合系统响应的均值为

(14)

由式(13)明显看出，车桥耦合系统响应的均值是由确定性荷载项F1(t)引起的确定性荷载项。

在构造虚拟激励响应过程中，假设轨道高低不平顺为零均值平稳过程，则车桥耦合系统响应的均值为

(15)

由式(15)明显看出，车桥耦合系统响应的均值是由确定性荷载项F1(t)引起的。

车桥耦合系统响应的方差矩阵为

(16)

根据维纳-辛钦关系，式(16)可转化为

(17)

式中:Suu为车桥耦合系统响应的自功率谱矩阵。

因为本文已经假设轨道不平顺为零均值的平稳随机过程，所以第i个轮对所在位置处的轨道不平顺为

F(t)=[F(t-τ1)F(t-τ2)F(t-τ3)F(t-τ4)]T

(18)

则构造的车桥耦合系统虚拟激励可表示为

(19)

式中：Q=(e-iwτ1e-iwτ2e-iwτ3e-iwτ4)T。

由2.1和2.2节可知，车辆系统空间模型独立自由度总数为6个，RC桥梁系统每个单元节点自由度也为6个，然后将轨道高低不平顺作为激励源，采用虚拟激励法建立系统分析模型，构造虚拟激励，运用分离迭代法求解车桥耦合系统振动方程，从而进行车桥系统空间随机振动的研究。

2.3.3 车速对车桥时变耦合振动的影响

以青藏铁路客运专线某三跨32 m简支梁为例，计算车辆采用中国CRH380A型高速列车，采用德国低干扰谱分析车辆桥梁垂向系统随机动力响应，建立简支梁垂向车桥耦合动力方程，利用 MATLAB软件编制车桥垂向耦合振动程序。

随着列车车速的增加，车桥耦合振动呈现不同的响应规律，因此，本文将列车车速划分为7个等级，平均每60 km/h表示1个等级。图4所示为列车在60 km/h～420 km/h不同速度等级下，通过RC桥梁时的列车垂向振动加速度响应概率密度曲线；图5和图6分别所示为列车在60 km/h～420 km/h不同速度等级下，通过RC桥梁时的列车垂向振动位移和垂向振动加速度的均值与标准差。

图4 中跨跨中列车垂向加速度响应概率密度分布

图5 中跨跨中列车垂向振动位移分布

图6 中跨跨中列车垂向振动加速度分布

由图4可知：随着列车车速逐渐增加，中跨跨中列车垂向振动加速度响应概率密度曲线峰值也向右移动，与此同时，中跨跨中列车垂向振动加速度响应概率密度曲线峰值逐渐减小，但是，中跨跨中列车垂向振动加速度响应分布范围却变得增大，这种情况与图6中中跨跨中列车垂向振动加速度响应均值及标准差的分布状况完全相符。由图4～6得出：随着列车车速逐渐增加，中跨跨中列车垂向车桥耦合振动响应均不同程度增大，不论是列车垂向振动加速度均值和标准差还是列车垂向振动位移的均值和标准差，它们都同时在列车运行速度达到300 km/h时达到最大，也就是说在列车运行速度达到300 km/h时出现响应峰值，造成这种状况的主要原因为：当本文选取的CRH380A型高速列车以300 km/h的运行速度通过青藏铁路客运专线三跨32 m桥梁时，在轨道不平顺激励下，桥梁在荷载的作用下发生强迫振动，此时，该RC桥梁的一阶自振频率与列车所发生的强迫垂向振动频率基本相等，因此，系统发生车桥耦合共振。

3 荷载影响因子的确定

合理地确定荷载影响因子有利于科学评定氯离子侵蚀下RC桥梁的承载力和使用寿命。文献[16]中分别对潮汐循环、水下区和近海大气区3种环境下的试验结果进行二次多项式拟合，得到荷载影响因子。但是，该方法仅考虑桥梁的本身载荷而未考虑列车重量及其运行速度，因此，该方法的结果不适用于RC桥梁Cl离子扩散模型中。本文基于能量守恒定律计算列车运行于RC桥梁上时的荷载影响因子。

3.1 假定条件

列车以不同速度运行于RC桥梁时，RC桥梁结构上的应力和变形分布比较复杂，因此，精确地计算振动引起的冲击载荷、荷载影响因子及被振动冲击RC桥梁结构中由振动冲击载荷引起的应力和变形非常困难。本文采用简化计算方法，并且提出假设条件：①假设列车的变形忽略不计，即认为列车是刚体。从开始振动冲击到振动冲击产生最大位移时，列车与RC桥梁结构一起运动，而不发生回弹；②认为列车振动冲击载荷引起的应力和变形在振动冲击瞬间遍及被冲击RC桥梁结构，并假设被冲击RC桥梁结构仍处于弹性范围内；③假设振动冲击过程中没有其他形式的能量转换，机械能守恒定律仍然成立。

3.2 能量守恒定律的应用

列车运行于RC桥梁时，由于轨道不平顺引起的垂向振动过程，如图7所示。

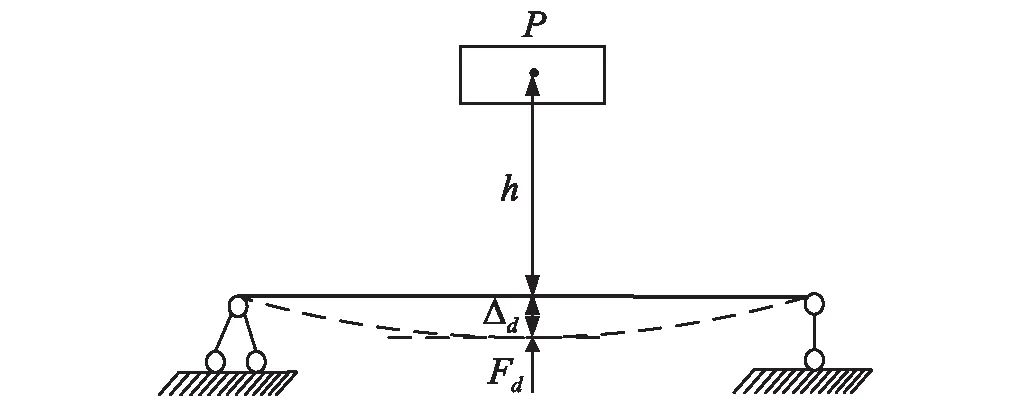
图7 列车垂向振动过程简图

图7中，h表示高速列车车体质心振动下降位移，即图2中的一系和二系弹簧压缩位移之和；Δd表示列车振动载荷引起的RC桥梁的最大位移；Fd表示最大振动载荷。则列车振动过程对应的能量转换过程就是列车机械能(势能)转换为RC桥梁结构弹性能，如下式所示。

机械能(势能)

E=P(h+Δd)

(20)

弹性能

(21)

由能量守恒定律可得E=Vδ，则有

(22)

由式(22)可得

(23)

在式(23)中，令Δst=P/δ，表示静位移。那么式

(23)转化为式(24)。

(24)

由式(24)可得

(25)

则得到最大振动载荷

(26)

3.3 荷载影响因子确定

实际工程中，RC桥梁上每天有列车运行，而且随着列车车速逐渐增加，跨中列车垂向车桥耦合振动响应均不同程度增大，因此，在推导RC桥梁氯离子扩散修正模型时，必须引入影响氯离子扩散的荷载影响因子f(δ)，从而得到式(8)考虑荷载影响因子的RC桥梁氯离子扩散修正模型，则由式(26)得到荷载影响因子f(δ)，如式(27)所示。

(27)

由式(27)可知，荷载影响因子f(δ)是大于1的系数，它表示RC桥梁结构承受的振动载荷是静载荷的若干倍数，它的取值与列车垂向振动位移h及列车车体质量有关，可由本文第2节内容仿真结果得出，列车运行速度直接决定了列车垂向振动位移h的大小， 因此，得到考虑列车以不同速度运行于桥梁上时，荷载影响因子f(δ)的数学表达公式，用于计算既考虑Cl离子锈蚀又考虑列车运行速度情况时，RC桥梁整体结构多龄期时变车桥耦合振动使用寿命曲线，最后预测得到RC桥梁的使用寿命。

4 RC桥梁结构使用寿命预测结果

4.1 预测模型中相关参数确定

基于国内外研究成果，本文针对盐湖地区Cl离子锈蚀环境下，列车速度提高及RC桥梁超载现象日趋严重的现状，对RC桥梁结构使用寿命预测模型中相关参数的取值进行分析。

4.1.1 荷载影响因子

随着青藏铁路列车不断提速和客、货运车辆流量增加，造成青藏铁路沿线部分RC桥梁的病害发展速度加快。如何科学合理地确定荷载影响因子将有利于综合评定桥梁的承载力和使用寿命。

4.1.2 氯离子扩散系数的时间依赖性系数

文献[17]对于不同环境下的氯离子扩散系数的时间依赖性系数进行了详细总结，基于该总结，鉴于RC桥梁结构的高性能特性，本文氯离子扩散系数的时间依赖性系数取m=0.64。

4.1.3 RC桥梁结构氯离子结合能力及劣化效应系数

综合国内外的研究成果，RC桥梁结构氯离子结合能力参数R的取值为R=3～8，为了安全，本文取R=5；根据文献[2]，将混凝土氯离子扩散性能的劣化效应系数的取值确定为：K= 2.0。

4.2 预测模型计算与仿真

4.2.1 预测模型计算

采用本文2.2.3节的简支梁和青藏高速铁路线上运行的某型高速列车为目标，利用MATLAB 软件对本文所提方法的预测模型进行数值计算，得到预测模型对青海盐湖地区氯离子侵蚀环境下，列车以不同速度运行时RC桥梁的使用寿命。

4.2.2 仿真实验验证

2017年7月实验室制作了3块与RC桥梁材料相同的混凝土立方体试件，并将其置于特制的与青海盐湖地区Cl离子浓度相同的环境中，从2017年9月开始，按照10次/天的频率用激振器对该3块混凝土立方体试件分别施加不同的振动载荷，将3块试件分别编号为1、2、3，在3块试件上用MATLAB软件和激振器仿真列车速度所施加的垂向振动载荷，在试件1、2、3上分别施加的振动载荷等效于v=120 km/h、v=300 km/h、v=360 km/h所产生的垂向振动位移和加速度，直至2018年3月8日。然后对该3块混凝土立方体试件采用钻芯法采集粉末样品，用化学分析方法测定了混凝土试件不同深度的自由氯离子质量浓度分布情况。预测模型计算和实验验证结果，如图8所示。

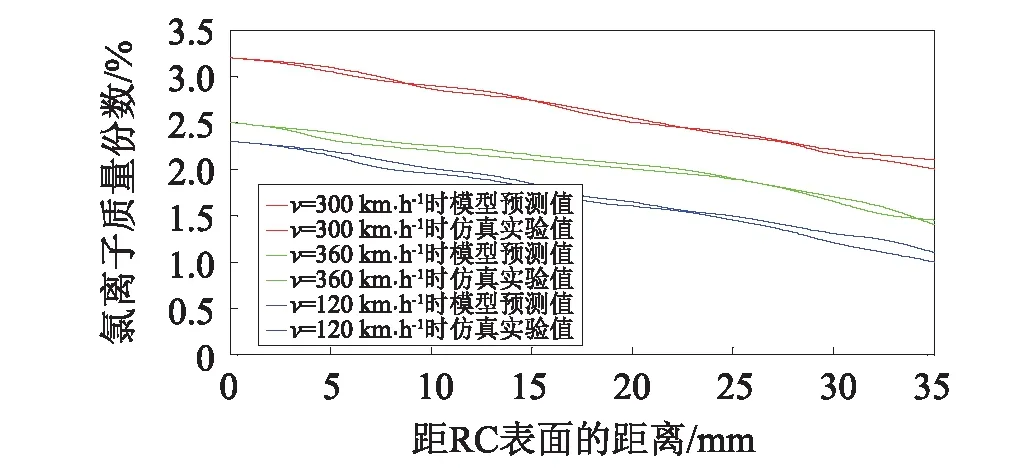
图8 预测模型计算和实验验证结果

由图8表明，不论是列车以v=120 km/h、v=360 km/h还是v=300 km/h的速度通过RC桥梁时，用本文理论模型获得的氯离子浓度预测值与仿真测值基本上一致。在盐湖地区氯离子侵蚀环境中，当列车分别以v=120 km/h、v=360 km/h、v=300 km/h的运行速度常年通过RC桥梁时，RC桥梁表面、深度20 mm及35 mm处氯离子浓度理论预测值和仿真测值，如表1所列。

表1 氯离子浓度值

由表1可知，随着列车速度的逐渐增加，RC桥梁构件中氯离子浓度也逐渐增大，当列车速度达到v=300 km/h时，RC桥梁构件中氯离子浓度达到最大，这种情况是由于车桥耦合共振所导致。

基于表1中氯离子理论预测值，再结合模型各参数值，通过式(9)分别计算列车以v=120 km/h、v=300 km/h和v=360 km/h的速度运行于RC结构桥梁时，其RC结构桥梁的使用寿命，分别可达到98.3 a、76.6 a和96.1 a。

5 结 论

(1)基于Fick第二扩散定律的理论、质量守恒定律和实际工程经验总结，充分考虑混凝土氯离子扩散系数的时间依赖性、轨道不平顺激励及高速列车运行速度对RC桥梁结构垂向振动的影响等因素，得到考虑荷载影响因子f(δ)及氯离子结合能力的RC桥梁氯离子扩散修正模型；

(2)以高速列车车体和RC桥梁为研究对象，建立RC桥梁车桥垂向耦合振动模型，基于虚拟激励法，利用MATLAB 计算平台编制车桥垂向耦合振动程序， 求解和分析了列车不同行驶速度对桥梁加速度响应的影响和垂向振动位移；

(3)基于能量守恒定律和列车垂向振动位移，确定了列车以不同速度在RC桥梁上运行时的荷载影响因子f(δ)的取值。最后，采用与RC桥梁材料相同的混凝土立方体试件，并将其置于特制的与青海盐湖地区Cl离子浓度相同的环境中，用激振器对该混凝土立方体试件施加振动载荷，从而对本文预测模型进行了仿真验证，取得了较好的验证效果；

(4)随着列车速度的逐渐增加，RC桥梁构件中氯离子浓度也逐渐增大，当列车速度达到v=300 km/h时，RC桥梁构件中氯离子浓度达到最大，这种情况是由于车桥耦合共振所导致。然后再分别计算列车以v=120 km/h、v=300 km/h和v=360 km/h的速度运行于RC结构桥梁时，其RC结构桥梁的使用寿命，分别达到98.3 a、76.6 a和96.1 a，从而证明了列车运行速度对氯离子侵蚀环境下RC桥梁结构使用寿命的影响。