超共振振动转子系统振动同步及同步传动

2019-07-08夏晓鸥王晓波

振动与冲击 2019年12期

陈帮，夏晓鸥，王晓波

(1.北京科技大学机械工程学院, 北京 100083；2.北京矿冶科技集团有限公司, 北京 100160)

自同步技术及相关设备已广泛应用于工业生产中[1-3]。振动自同步研究内容涉及非线性振动、机电耦合、自动控制理论等[4-8]。转子安装在可振动体上形成振动转子系统，两个振动转子系统的振动机体通过弹簧连接形成双振动转子系统，如图1所示。控制连接弹簧的刚度以及机体的运动轨迹，可转化为多种动力学系统，例如将连接弹簧趋于无限大，即为双转子固定于同一机体上的振动系统；将某一机体的运动轨迹设计为圆弧，即为摆动系统。讨论两个振动转子系统之间的耦合行为，对振动同步研究具有积极的学术意义。

近年来，Peňa、Jovanovic、Dilao等[5-10]学者分析了不同参数对摆同步行为的影响，包括摆的同向及反向同步。Czolczynski利用节拍器研究两个及多个摆之间的耦合同步现象，讨论了系统的能量传递情况。Koluda等[11-12]研究了耦合摆之间的自同步行为。摆动同步理论不断丰富[13-15]，显示了摆动同步的多样性。Blekhman等[16-17]首次研究了转子自同步现象，得出了安装在同一机体上转子自同步的条件。Wen等[18]发展了振动自同步的研究，研究成果应用于工业生产，取得了良好效果。Zhao等[19-21]采用改进小参数法研究振动自同步，讨论了多种类型振动系统的转子同步行为。刘劲涛等[22]研究了反共振机械的振动同步问题。李凌轩等[23]研究了双机振动系统分别在亚共振与远共振条件下的同步性问题。Zhang等[24-27]分别研究了三转子振动系统的同步行为。同时，侯勇俊设计了双转子椭圆振动机，Fang[28]分析了该系统的转子耦合摆动力学行为。

上述研究多侧重于安装在同一振动体上的摆或转子同步研究，对于振动转子系统的耦合同步研究较少。作为高频双动颚振动破碎机的理论模型，超共振双振动转子系统的同步特性随耦合弹簧刚度的变化情况尚不明确。针对该问题，本文拟利用动力学方法研究系统的振动情况，阐明系统的振动同步与振动同步传动特性；以振动力矩为切入点，深入讨论耦合弹簧对系统同步的影响，揭示该系统实现高稳定性与高容差性的耦合机理，为开发高可靠性振动设备和激振系统提供参考。

1 双振动转子系统

如图1所示，转子1和转子2分别安装在振动体1和振动体2上。弹簧kp两端分别固定在两个振动体上，阻尼记为fp。m1，m2分别表示转子质量，φ1，φ2分别表示转子连杆与水平方向的夹角。转子对应的驱动力分别为Te1，Te2，阻力分别为Tf1，Tf2，阻尼系数分别为fr1，fr2。令转子逆时针方向转动为正。振动体可在水平方向上运动，质量为M1，M2，位移分别表示为x1，x2，与地基连接弹簧刚度与阻尼分别为k1、f1、k2、f2。转子关于质心的转动惯量分别为j1，j2，偏心距分别为r1，r2。

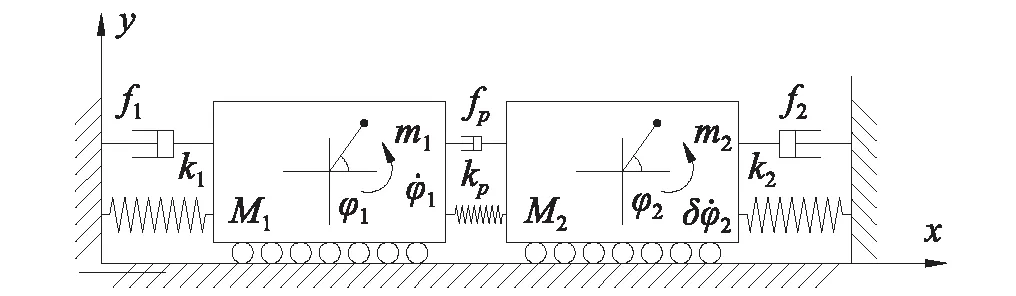
图1 双振动转子振动模型

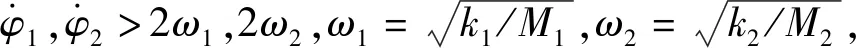
其中：

势能与耗散函数分别为

式中：ni，Lmi，ωsi，Lsi，Rri分别对应电机的极数、互感系数、同步转速、定子电感、转子电阻；U0为电机电网的电压幅值。建立系统的振动微分方程如下

(1)

2 同步研究

由式(1)可知，所研究模型是刚度耦合的振动系统。由转子自同步的相关定义可知，转子实现振动自同步时，系统稳定运动，速度波动较小。为简化计算并考虑实际工业应用，系统的弹簧阻尼均很小，弹簧k1与弹簧k2的阻尼相同。根据学者Blekhman的研究，忽略小变量。在一阶近似条件下简化式(1)得

(2)

其中

(3)

系统同步转速为ωn，记转子的相位如下

φ1=ωnt+α,φ2=ωnt+α2

(4)

如上节说明系统运行远离共振区，α1，α2为慢变函数。由式(2)～(4)得

x1=a11cos(φ1+γ11)+a12cos(φ2+γ12),x2=a21cos(φ1+γ21)+a22cos(φ1+γ22)

(5)

式中

(6)

a11,a12,a21,a22体现了振动体之间、转子之间、转子与振动体之间的耦合作用。显然，a12，a21越大，振动转子之间的耦合作用越强。根据转速与振动固有频率关系，可分为前共振(ωn<ω1,ω2)与超共振双振动转子系统(ωn>ω1,ω2)。考虑超共振双振动转子同步行为特性及其工业应用的特点，本文重点研究超共振双振动转子系统。

γ11,γ12,γ21,γ22是由于阻尼作用相应产生的相位滞后。由于研究模型为弱阻尼系统，相位滞后可计算为γ11=f1a11/(m1r1ωn)、r12=f1a12/(δm2r2ωn)、γ21=f2a21/(m1r1ωn)、γ22=f2a22/(δm2r2ωn)，其中γ12=γ21。

3 转子的同步性及其稳定性

利用平均法将快变运动(高频)与慢变运动(低频)分开讨论，是分析非线性振动问题的一种实用手段。定义运算，若h(t)是周期函数，其在一个周期T上的平均值记为〈h(t)〉，如下式

(7)

转子同步运转时，转子所受的加速度平均值为0，或者合力矩在一个周期上平均值为0，因此

(8)

转子依靠电机驱动，电机的阻力近似与转速成正比。转子稳定旋转时，转速波动较小，由赵春雨，张学良以及方潘的研究可知，感应异步电机输出力矩的动态特性可线性化。因此在稳定转速附近，可用Tei(ω)，Tfi(ωn)代替〈Tei(ω)〉，〈Tfi(ω)〉进行讨论。系统同步稳定运行时，定义转子受到合力矩的平均值为P1，P2，则

(9)

(10)

由式(5)、(6)、(9)以及(10)得

(11)

令：

(12)

系统为弱阻尼系统，γ11、γ22为小参数，则式(9)，(10)可简化为

(13)

(14)

Tv为系统的振动力矩，作用在转子上调节转子之间的能量分配，是系统实现振动自同步的关键指标，其大小与转子的同步转速、振动体质量、支撑弹簧、耦合弹簧等参数有关。式(13)，(14)相减得

P1-P2=Te1(ωn)-Te2(ωn)-
[Tf1(ωn)-Tf2(ωn)]-Tv

(15)

定义

Δα=α1-α2-γ12,
ΔTe(ωn)=Te1(ωn)-Te2(ωn),
ΔTf(ωn)=Tf1(ωn)-Tf2(ωn)

(16)

由式(6)，(8)以及(15)得

(17)

定义系统同步指数D为

(18)

所以

(19)

若关于方程式(17)有实数解，要求式(17)右边的绝对值小于或等于1，所以系统实现自同步的条件为

|D|≥1

(20)

分析式(13)～(15)可知，振动力矩Tv是系统能否实现自同步的关键因素，其大小与耦合系数a12，a21相关，其值越大，系统越易实现自同步。可通过Lyapunov稳定性理论讨论系统同步的稳定性。双振动转子系统中有

P1-P2=ΔTe(ωn)-ΔTf(ωn)-Tv

(21)

系统可维持自同步运行状态的稳定性条件为

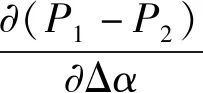
(22)

结合式(6)，(12)得：

(23)

式(23)即是转子自同步运行的稳定性条件。其稳定运行的状态与转子的转向相关，转子同向旋转与反向旋转的稳定运行相位差处于不同象限。

由上述讨论可知，系统稳定同步运行时，振动力矩可以作为驱动力作用在转子上，若该驱动力矩足够大，能够克服转子受到的阻力矩，则可关闭该转子的电机，在振动力矩的作用下转子依然保持同步转动，即实现振动同步传动。若在系统稳定运行后，只开启转子i(i=1,2)的驱动电机，系统可保持振动同步转动，对应同步指数为DTi，式(18)变为

(24)

系统稳定运行后，只开启转子i的驱动电机，系统能够实现振动同步传动的条件为

|DTi|≥1

(25)

电机的开启或关闭并没有体现在稳定性条件式(23)中，因此稳定性条件仍为式(23)。

4 模型讨论

双转子振动系统是两个振动系统间的耦合动力学模型。在一定条件下，系统满足自同步条件，即使电机、转子质量、偏心惯量、振动体质量等振动参数有明显差异，仍可实现同步旋转。根据公式(6)、(20)、(23)以及(24)，控制连接弹簧的刚度，可直接增强或降低系统之间的耦合作用，使系统在不同状态下同步运转，并具有一定的稳定性。本文讨论模型的相关研究数据，如表1所示。

表1 系统动力学参数

振动体之间通过弹簧连接，不同于两个振动体固定在一起，特点是通过弹簧代替刚体连接，由系统的同步方程式，可直观认为，在不改变其他参数的情况下，可通过连接弹簧控制振动力矩的大小。自同步现象是振动力矩与转子输入转矩之差共同作用的结果。显然的，耦合弹簧kp的大小会影响系统之间耦合作用，表现出对振动力矩传递效率的影响。分析式(6)与(12)，有如下关系式：

(26)

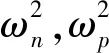
(27)

(28)

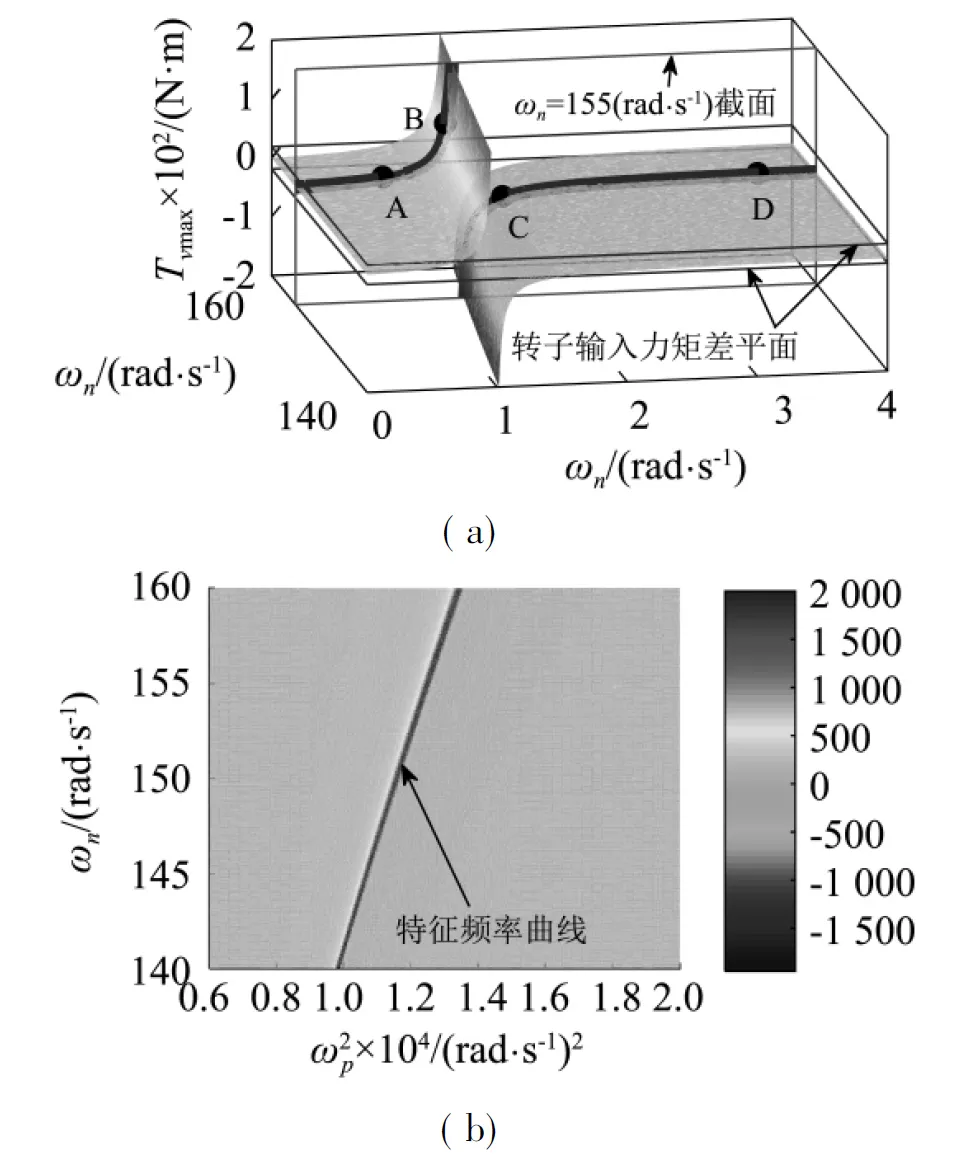
图3 ωn=155 rad/s时最大振动力矩关于耦合频率的关系

当ωp→+∞，即kp→+∞，则：

(29)

(30)

式(19)为

(31)

相应的转子实现自同步的稳定性条件根据式(22)可得：

(32)

由于最大振动力矩关于耦合频率的变化，在特征频率右部是连续单调递增的，因此可以认为，在两个振动体相互固定时，其最大振动力矩达到极限Tv max lim。

图2，图3以及上述分析表明，系统耦合频率在特征频率附近时，或系统参数状态在特征曲线附近时，系统耦合性能强，易实现振动自同步。调节连接耦合弹簧的大小，可改变最大振动力矩的大小，从而控制系统的同步性能与同步状态。安装于同一振动体上的双转子振动系统同步行为，可以认为是双振动转子系统中连接弹簧趋于无限大的一种特殊情况。在超共振系统中，两个转子之间通过刚体连接(两个转子安装在同一机体上)的耦合性能并不是最大。该结论的意义在于，在单质体或双质体双转子同步振动系统中，当两个转子难以实现振动自同步时，可设计将原本安装在同一机体上两个转子，安装在具有一定刚度的柔性体上，或者分别安装在两个通过弹簧连接的机体上，控制耦合频率，可以增强系统的耦合作用。此时系统可获得更为宽松的振动同步条件，稳定性与容差度可进一步提升。

5 同步性数值仿真

(a)

(b)

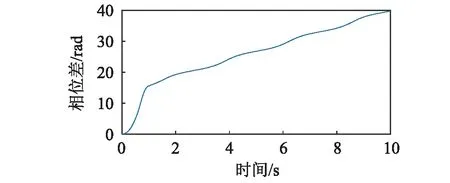
图4显示了连接弹簧刚度kp为1.36×106N/m时，转子的运动状况。分析图2，图3及式(19)可知，该状态下，转子输入力矩之差的绝对值|ΔTe(ωn)-ΔTf(ωn)|大于振动耦合所产生的最大振动力矩|Tv max|的绝对值，式(19)无实数解，不存在振动自同步状态。由图4(a)可知，转子1与转子2的转速在稳定运转时不相同，图4(b)显示转子的相位差逐渐增大。

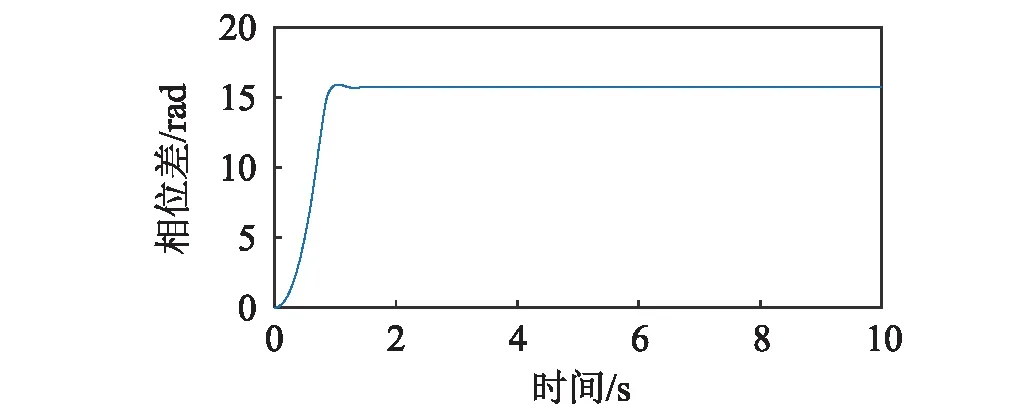
图5显示了连接弹簧刚度kp为2.32×106N/m时，系统的振动情况。分析图2，图3及式(19)可知，该状态下，转子输入力矩之差的绝对值|ΔTe(ωn)-ΔTf(ωn)|小于振动耦合所产生的最大振动力矩|Tv max|的绝对值，满足系统的振动自同步条件。由式(17)及式(23)计算相位差得Δα=3.28 rad。图5(a)表明转子1与转子2的转速在系统稳定运转时趋于相同，在1.4 s左右实现振动同步；图5(b)显示转子的相位差稳定在15.83 rad(15.81-4×π=3.26 rad)。数值分析与理论分析基本一致。图6显示了连接弹簧刚度kp为3.2×106N/m时，转子的运动状况。同样的，该状态满足系统振动自同步条件。理论计算得Δα=3.65 rad。由图6(a)可知，转子1与转子2的转速在1.4 s左右实现振动同步；图6(b)显示转子的相位差稳定在16.20 rad(16.20-4×π=3.63 rad)。数值分析与理论分析基本一致。

(a)

(b)

(a)

(b)

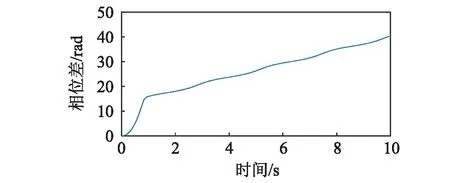
连接弹簧刚度kp为7.12×106N/m时，转子的运动状况如图7所示。由图2，图3及式(19)可知，此时系统不满足系统的振动自同步条件。图7(a)显示了转子1与转子2的转速在稳定运转时不统一，图7(b)显示转子的相位差逐渐增大。连接弹簧刚度趋于无穷大时，转子的运动状况如图8所示。同样，该状态不满足系统的同步条件。由图8(a)可知，转子1与转子2的转速在稳定运转时不同步，图8(b)显示转子的相位差逐渐增大。

(b)

(a)

(b)

6 振动同步传动数值仿真

(a)

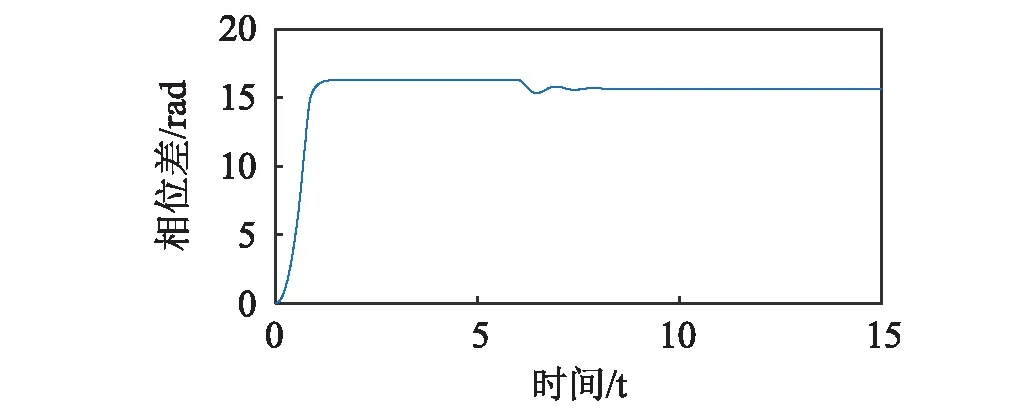
(b)

(a)

(b)

图9显示两个转子在开机后2 s附近时实现振动自同步，转速一致为ωn=154.67 rad/s。在6 s时，去除转子1的驱动，经过耦合作用，转子1与转子2仍可保持同步运转，转速较之前略有降低，相位差回落；此时ωn=153.15 rad/s，Tv max=-29.17 N，ΔTe(ωn)-ΔTf(ωn)=0.6162 N，满足式(25)的同步条件。图10显示了系统转子实现自同步运转后，在6 s时，去除转子2的驱动，经过耦合作用，转子1与转子2同样可保持同步运转，转速较之前却有增加，相位差相应发生变化；此时ωn=155.99 rad/s，Tv max=-34.85 N，ΔTe(ωn)-ΔTf(ωn)=1.41 N，满足式(25)的同步条件。系统转子实现自同步运转时，振动力矩Tv平衡两个转子的能量输入差ΔTe(ωn)-ΔTf(ωn)，作用在落后的转子上为驱动力矩，作用在超前的转子上为阻力矩。在特定条件下，超前转子的驱动电机不仅输出能量维持系统的振动，还输出能量至落后转子的驱动电机。此时，落后转子的驱动电机实际上吸收能量。若两个转子可实现振动同步传动，将落后转子的电机从系统中去除，则该电机不会从系统中吸收能量，系统因此会获得较多能量，同步转速反而提高；若将超前转子的电机从系统中去除，则落后电机需向系统中输出能量维持系统振动，输出力矩为正，转速因而降低，相位差发生变化。若系统的阻尼较大，两个转子的输出力矩均为正，则在振动同步传动时，同步转速均会降低。

7 结论

(1)超共振双振动转子系统是一种具有自同步特性的振动系统，控制系统参数可转化为不同类型振动系统。在一定条件下，超共振双振动转子系统具备良好的自同步性能，具备高稳定性、高容差度的特点。耦合频率ωp在特征频率附近时，或系统参数状态在特征曲线附近时，系统所产生的振动力矩大，转子易实现振动自同步。双转子固定于同一机体的振动系统，可认为是系统连接弹簧趋近无穷大时的一种特定情况。

(2)通过调节连接耦合弹簧kp的大小，可控制系统的同步性能。超共振双振动转子系统不仅可以实现转子的振动自同步，也可实现振动同步传动。若系统参数满足相关条件，在转子实现振动自同步后，切断一个电机的电源，系统仍可实现振动自同步。

(3)对比B、C点以及ωp→+∞，可知在超共振系统中，两个转子之间通过刚体连接(两个转子安装在同一机体上)的耦合性能并不是最大。该结论的工程意义在于，安装在一个机体上的双转子振动系统，若两个转子难以实现振动自同步，可考虑两个转子安装在柔性体上，或者两个通过弹簧连接的机体上，调节两个振动体支撑弹簧与耦合弹簧的刚度大小，使系统具有更为宽松的振动同步条件。利用该原理设计振动系统可具有良好的稳定性与容差度。