距离和的最小值公式及其应用

广东省珠海市拱北中学(519020)崔志锋

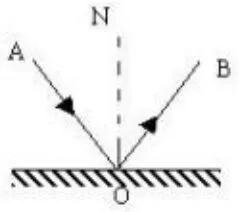
图1

在初中数学教学中,总会遇到类似“饮马问题”、“造桥选址问题”之类的问题.抽象成数学问题就是,在一条定直线上确定一点,使到直线同侧两定点的距离和最小.在中考数学中,还会遇到已知一个或两个定点,在两条相交直线上各确定一点使它们的距离和最短.例如:2011年广东深圳23 题第(2)题和2011年福建福州22 题第(3)题.这类问题在数学上要考察的知识点有两点之间线段最短、垂线段最短、点关于线对称等.大家也都清楚它们的做法(做点关于直线的对称点,连结另一点与对称点或对称点与对称点即可).在此,我想换一个角度来分析它,并得到一些相关的公式,以便在一些实际工程问题中也能得到应用.这让我想起物理光学中所讲的光是沿直线传播和光的反射定律.如图1,ON是法线,AO是入射光线,OB是反射光线,则有AO,ON,OB在同一平面,AO,OB会在法线ON两侧,且∠AON=∠NOB.

我们先来看看下面两个问题:

问题1已知同一平面内一条定直线l和直线l同侧的两个定点A和B,直线l上存在唯一一点P,使得PA+PB的值最小.

问题2已知一块固定的平面镜l,在镜子正上方有两个定点A和B,平面镜l上存在唯一一点P,使得以AP为入射光线经平面镜l反射后也经过点B.

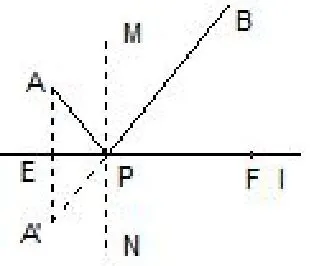
图2

这两个问题是等价的.首先易证这两个问题的存在唯一性.现在第一步假设问题1 成立.如图2,点A′是点A关于直线l的对称点,PA+PB的值最小时,A′、P和B三点共线,所以∠APE= ∠EPA′= ∠BPF,又因为MN⊥EF,所以∠APM= ∠MPB,故以AP为入射光线经直线l反射后也经过点B.第二步假设问题2 成立.如图2,以AP为入射光线经直线l反射后也经过点B,则由平面镜成像原理得点A关于直线l对称点A′、P和点B共线,而两点之间线段最短,所以PA+PB的值最小.证毕.

现在可以把如何在直线l上确定一点P,使PA+PB的值最小的问题,转换成如何确定一个入射角的光线AP,使得它经直线l反射后经过B点.下面分三种类型来讨论.说明:以下讨论的光线都是指从点A出发,经一次或两次反射后从点B出来.入射角x指的是第一次反射的入射角,入射角y指的是第二次反射的入射角.

类型一、两个定点和一个动点

定理1如图3,已知两个定点A和B,OA=a,OB=b和∠COD=α(0° ＜α ＜90°),入射角为x,则PA+PB的最小值且入射角x满足

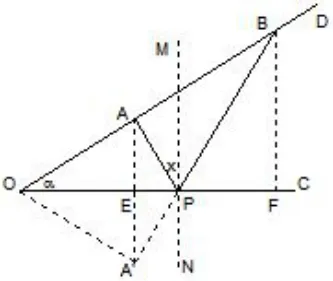
图3

推论若已知AE⊥OC,BF⊥OC,AE=h1,BF=h2和EF_=d,入射角为x,则PA+PB的最小值Smin=且入射角x满足

定理1 的证明如图3,作点A关于OC的对称点A′,连结A′B交OC于点P,连结AP,则∠A′OB= 2α,利用余弦定理得AA′= 2asinα,由2asinαsinx= (b-a)sin(90°-α-x)化简得

应用1如图4,在△ABC中,AC=BC=2,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值为____.

图4

解由题知,a=BD=1,b=BC=2,α=∠B=45°,则EC+ED的最小值

应用2如图5,一次函数y=kx+b的图象与x、y轴分别交于点A(2,0),B(0,4).设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时P点坐标.

图5

解由题知,DC=2,h1=h2=1,入射角x=∠PCO,则PC+PD的最小值所以∠PCO=45°,P(0,1).

类型二、两个定点和两个动点

定理2如图,已知两个定点A和B,OA=a,OB=b,∠AOC=α1,∠BOD=α2(0° ＜α1＜α2＜α1+α2＜ α)和∠COD=α(0° ＜ α1+α2+α ＜180°),入射角为x和y,则AQ+QP+PB的最小值且入射角x、y满足x+y=α和

图6

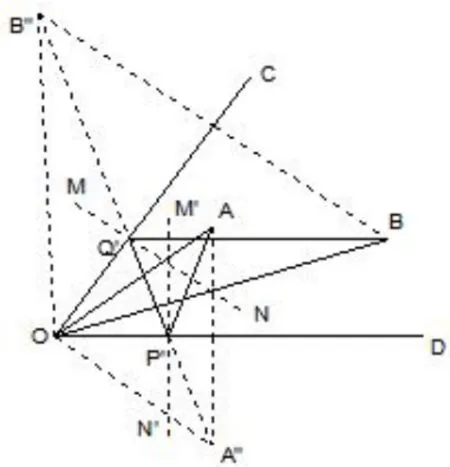
图7

证明如果光线如图6,则由余弦定理得到S21=A′B′=a2+b2-2abcos(α1+α2+α),如果光线如图7,记∠AOD=α′1,∠BOC=α′2(α′1+α′2＞α),则由余弦定理得到S22=A′′B′′=a2+b2-2abcos(α′1+α′2+α),因为S22-S21=2abcos(α1+α2+α)-2abcos(α′1+α′2+α)=所以S22≥S21,即S2≥由asin(90°-α1-x)=bsin(90°-α2-y)易得tanx=证毕.

推论1若已知定点B在OD上,OA=a,OB=b,∠AOC=α1(0° ＜α1＜α)和∠COD=α(0° ＜α ＜60°),入射角为x和y,则AQ+QP+PB的最小值Smin=且入射角x、y满足x+y=α和

推论2若已知定点A在OC上,定点B在OD上,OA=a,OB=b和∠COD=α(0° ＜α ＜60°),入射角为x和y,则AQ+QP+PB的最小值Ssain=且入射角x、y满足x+y=α和

应用3已知,如图8,二次函数图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:对称.过点B作直线BK//AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值.

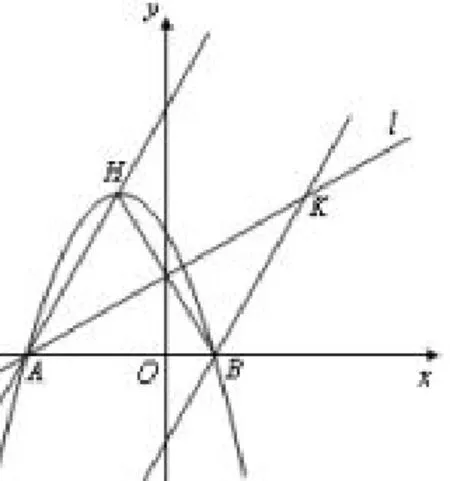
图8

解如图8,易知α= ∠HAK= 30°,则HN+NM+MK和的最小值是

应用4如图9,抛物线y=-(x -1)2+ 4 的 顶 点 为C,交x轴于A、B两点,交y轴于点D.过点A的直线与抛物线交于点E,交y轴于点F,其中点E的横坐标为2,若直线PQ为抛物线的对称轴,点G为直线PQ上的一动点,则x轴上是否存在一点H,使D、G、H、F四点所围成的四边形周长最小.若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由.

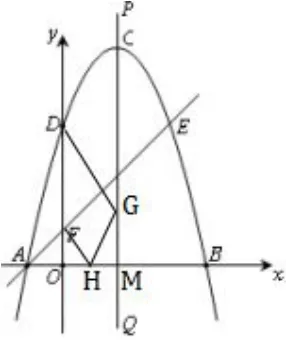
图9

解如图9,易知则周长最小值因为x= ∠HFO=∠HGM,所以所以G(1,1).

类型三、一个定点和两个动点

定理3如图10,已知一个定点A,OA=a,∠AOD=和∠COD=α(0° ＜ α1+α ＜90°),入射角为x,则AQ+QP的最小值Smin=asin(α1+α),且入射角x满足x=α.

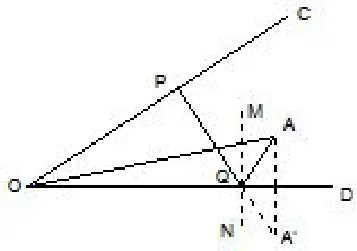
图10

证明方法同定理2 的证明.

推论若已知定点A在OD上,OA=a和∠COD=α(0° ＜α ＜45°),入射角为x,则AQ+QP的最小值Smin=asin 2α,且入射角x满足x=α.

应用5如图11,在锐角△ABC中,AB= 4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是____.

图11

解由题知,a=AB=4,α=22.5°,则BM+MN的最小值

应用6如图12,△ABC中,AB= 2,∠BAC= 30°,若 在AC、AB上各取一点M、N使BM+MN的值最小,求这个最小值____.

图12

解由题知,a=AB=2,α=30°,则BM+MN的最小值