注重多重样例提升解题效率——例析毕业总复习《圆柱与圆锥》样例教学的有效性

钱国平

毕业总复习阶段的“样例”课对学生掌握知识技能至关重要。在《圆柱与圆锥》的总复习中我注重多重样例，为提升解题效率做了有效的尝试，也收到了较为理想的效果。在复习《圆柱和圆锥》时，在预设经典样例的同时，与学生一起剖析样例的思路，让学生由此及彼，更加明确概念，掌握思维方法，启迪解题思路，培养思维能力，提高解题效率，有助于培养学生自我分析问题，独立解决问题的良好习惯。以下是应用样例进行复习的具体实施过程。

一、设计概念题时，突出重点，让学生从对概念的“一知半解”转变为“一清二楚”

（一）重点问题

在具体的计算过程中，好多学生往往在计算圆锥体体积时，丢了“三分之一”。

（二）具体策略

针对学生计算圆锥体体积时丢“三分之一”这个问题，我选取了有针对性的实验操作。

1.解决思路。

探索等底等高的圆锥体积与圆柱体积之间的关系，概括出圆锥体积的计算公式。在与圆柱体积的对比中明确圆锥体积计算时不能丢掉“三分之一”。

2.具体方法。

（1）正例强化：在圆锥形容器里装满水，然后把水倒入与圆锥形容器等底、等高的圆柱形容器中，要倒几次才能恰好注满圆柱形容器？

（2）反例突破：然后再出示高相等、底不同或者高不同、底相等的实验，进一步证明必要条件是“同底等高”。

从这个实验里我们得出：圆柱形容器的体积是和它等底、等高的圆锥形容器的3 倍；反过来说，圆锥形容器的体积等于和它等底、同高的圆柱形容器的

二、设计计算题时，突破难点，让学生对计算题由“一错再

错”转变为“一网打尽”

（一）难点问题

圆锥的体积的整理和复习类同于前面圆柱体体积的复习，但跟圆柱有区别的是，这里先让学生根据旋转轴想象出两个不同的圆锥——学生的思维停留在轴与水平面垂直的旋转（图2），而没有考虑轴与水平面平行的旋转（图1）。

（二）具体策略

1.解决思路。

教师要引导学生“种出”这两棵不同的“树”，再根据学生想象所得的图形，分别计算它们的体积，最后再出示图形来验证想法是否正确。这样可以更好地发展学生的空间想象能力，培养学生的实证能力和习惯。

2.具体方法。

（1）出示用来旋转的基本图形。

（2）用基本图形旋转出新图形。

（3）分别计算旋转成的新图形。

图1

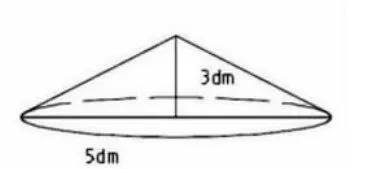
图2

师：你发现了什么？

生：同一个直角三角形，通过旋转，得到两个不同的圆锥，体积是不一样的。

（4）对比交流中实现拓展延伸。

圆柱和圆锥之间有很多的联系和区别，现在你能给下面的四个图形找找联系吗？

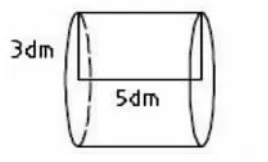
图1

图2

图3

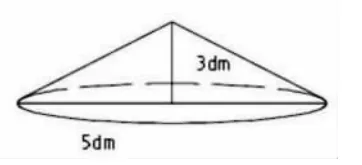
图4

引导学生得出：图1和图3等底等高，图2和图4等底等高；圆锥的体积分别是圆柱体积的圆柱体积分别是圆锥体积的3 倍。

通过以上这些直观演示、形象比较和有针对性的练习，学生计算出错率明显降低，收效显著。

三、设计应用题时，突出疑点，使学生解题从“一筹莫展”转变为“一览无疑”

（一）重要疑点

二分之一高度的圆锥体积是原圆锥体积的几分之几？学生对于这样一个问题是有疑惑的，如果没有比较好的教学方式，学生是非常容易做错的。

（二）具体策略

1.解决思路。

通过两例非常有针对性、有共同点的案例分析，让学生清晰地明白：二分之一高度的圆锥体积是原圆锥体积的八分之一；或圆锥体积是它二分之一高度的圆锥体积的八倍。

2.具体方法。

（1）例1：实例中提炼规律。

如下图所示，圆锥形状的容器内盛有1.2 升水，水面高度正好是圆锥高度的一半，这个容器里还能装多少升水？（水面高为，水面半径为）

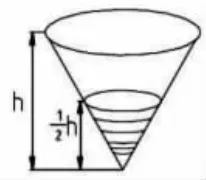
容器还能装水1.2×（8-1）=8.4（升）。

（2）例2：实例中应用规律。

通过以上两例非常有针对性、有共同点的案例分析，让学生清晰地明白：二分之一高度的圆锥体积是原圆锥体积的八分之一；或圆锥体积是它二分之一高度的圆锥体积的八倍。

四、设计思考题时，突出考

点，促学生由“一头雾水”转变为“一目了然”

（一）重要考点

例：把一个棱长为8dm 的正方体木料加工成一个最大的圆柱体，求其体积。

大多数学生对这个题目会感到一头雾水，不理解“最大”是什么意思，无从下手。

（二）具体策略

1.解决思路。

对于这样的例题，我们解决考点的最好办法就是让学生亲身体验，利用具体的实物让学生感觉例题图形的产生过程，有利于后续的正确解答。

2.具体方法。

通过具体的实物演示，进行模拟的切割，让学生明明白白知道“最大”的意思，那么求体积也就迎刃而解了。

圆柱的最大底面积：

3.14×（8÷2）2

=3.14×16

=50.24（平方分米）

圆柱的最大体积：

50.24×8=401.92（立方分米）

答：圆柱的体积是401.92 立方分米。

经过具体的实践，我们更加发现了样例学习的优越性，主要表现在以下四个方面：

其一，样例学习能够减轻学生的认知负荷，因为样例学习易化了认知技能的获取，克服了抽象信息难以获取的局限。特别是在几何知识的教学中，对于学生正确理解相关问题非常有利。

其二，样例学习可以帮助全体学生正确归纳所学规则，并根据问题的解决方法进行分类。能让学生把注意力集中在已知条件、未知条件、当前问题的状态上，引起注意力的高度集中。

其三，样例学习有助于节约教学时间和解题时间。学习一个解答好的样例比自己亲自去解决一个问题更简洁、更灵活。如果能长期坚持样例教学，学生就可以一类一类地进行学习和巩固相关知识。

其四，样例学习改变了让学生被动接受解题方法的现状，极大地调动了各个层次学生的学习积极性，学生对自己的学习能力和解题能力的提升更有信心。