夯实基础融通方法
——《立体图形的表面积和体积总复习》教学设计(一)
2019-07-06胡胜平
胡胜平
【教学内容】
苏教版六年级下册第94、95 页。
【教学过程】
一、以式想形,沟通图形之间的联系
课件出示:V=Sh S=S侧+S底×2。
师:看到这两个公式,你想到了可以求哪些图形的体积和表面积?请你写在练习纸上。
学生独立完成,教师巡视,并收集学生作品,投影反馈。
集体交流:
1.梳理体积公式。
学生基本上都会认为“圆柱、长方体、正方体”的体积可以用“V=Sh”来解决。提问:为什么这些图形的体积都可以用这个公式来计算?追问:圆锥的体积是否也可以这么求?最后请学生想象,怎样的图形可以用“V=Sh”来求体积?得出结论:能用这个公式求体积的立体图形是上下底面大小相等的直柱体。
2.沟通表面积公式。
教师出示两份学生作品,请学生比较,并说说自己的想法。


教师根据学生的回答,适时拿出长方体模型,请学生上来指一指侧面积,帮助学生理解:虽然这三种立体图形都有自己的表面积公式,但是都可以转化为“S=S侧+S底×2”来进行计算。
请学生再静静地思考:这些图形的侧面展开图是什么形状的?并将这些图形的侧面展开图贴在黑板上,追问:这些长方形的面积该怎么求?
教师根据学生的回答,将S=S侧+S底×2 进一步转化为S=Ch+S底×2。
小结:这些立体图形虽然形状不同,但相互之间有着密切的联系,所以它们的体积和表面积都可以用相同的方法来计算!
【设计意图:很多教师在设计这节复习课时,习惯采用“根据图形分类→说联系→说区别”这样的线路将前面的基础知识进行梳理。我在设计时则反其道而行之,让学生根据“V=Sh、S=S侧+S底×2”这两个公式猜测立体图形,然后沟通直柱体体积和表面积的一般公式,再进一步将“S=S侧+S底×2”转化到“S=Ch +S底×2”。经过这样的设计,将原本“形”不相同的立体图形联系到了一起。通过两次想象,让学生发现它们的共同点,然后将各自的体积公式、表面积公式都转化成同一个公式,沟通了图形之间的联系,培养了学生的空间想象能力。】
二、查漏补缺,夯实解决问题的基础
教师课件出示题组,要求学生独立完成,并思考每一个问题实际上要求的是什么,再进行连线。
学生独立完成,教师巡视,并收集学生作品,投影反馈。
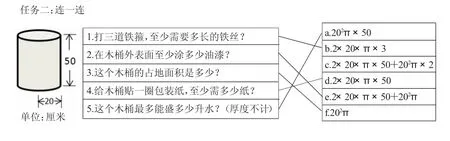
反馈时以开火车的形式,让学生说说选择连线的理由,并引导学生发现a 选项其实也是错的(没有进行单位换算)。
再出示另一份学生作品,请学生比较有什么不同,引导学生在今后的解决问题中,一定要先明确问题的指向,再进行计算。
小结:看来我们在解决问题时首先要弄清求的是什么,然后再具体问题具体分析,最后还要注意一些小细节,这样我们的解题正确率就会提高很多。
【设计意图:作为一节复习课,夯实基础是目标之一。在立体图形的表面积和体积的复习中,知识点多且零碎。因此,我设计了一组练习,将底面周长、表面积、底面积、侧面积、体积等多个“点”串联起来,学生在练习之前要先弄清每个问题的指向,再去动手解决。同时,有些问题还要根据实际情况进行具体分析,例如表面积中算一个底面还是两个底面的问题、容积和体积的关系、单位换算等问题。要让学生养成遇到问题先分析的习惯,而不是拿到数字就盲目计算。通过这样的练习,帮助学生查漏补缺,发现自己平时作业的“小问题”,为后面的拓展延伸打下扎实的基础。】
三、化繁为简,感受策略方法的灵活
1.比表面积,暗藏方法。
教师课件出示两块积木,请学生比较哪块积木涂色的面积大,并把想法写在练习纸上。

学生独立完成,教师巡视,并收集学生作品,投影反馈。
预设1:直接计算。正方体表面积=4×4×6=96(平方厘米),长方体表面积=(5×3+5×4+3×4)×2=94(平方厘米),96>94,所以正方体的表面积大!
预设2:利用S=Ch+S底×2 进行比较。长方体的底面周长是(5+3)×2=16(厘米),正方体的底面周长是4×4=16(厘米),且两个图形的高都相等,要比较它们的表面积,实际只需要比较它们的底面积即可。长方体的底面积为5×3=15(平方厘米),正方体的底面积为4×4=16(平方厘米),16>15,所以正方体的表面积大!
小结:看来比较这两个立体图形的表面积不但可以用以前的公式直接计算,还可以用S=Ch+S底×2 来比较。重要的是选择合适的方法!
【设计意图:相对于体积,表面积的计算更为繁琐,学生错误率也高。因此,设计了正方体和长方体两个图形让学生进行实打实地计算比较。在数据设计上,为了与整理环节相呼应,除了设计高相等,还设计了底面周长也相等。除了让学生知道可以利用直接计算比较出结果,还要引导学生发现这两个图形的侧面积其实也相等,要比较表面积,有时并不需要算全,只要比较底面积的大小即可,为后面体积的比较埋下伏笔。】
2.比体积,巧选方法。
教师在课件中再增加两块积木,请学生快速找出体积最大的积木。

学生独立完成,教师巡视,并收集学生作品,投影反馈。
预设1:依旧是完整计算,教师要给予肯定。
预设2:利用正方体和长方体高相等,只需比较底面积,16>15,说明正方体的体积更大。然后再比较圆柱和圆锥,利用它们的底面积相等,只需要比较它们高之间的大小,发现圆锥的体积更大。最后比较正方体和圆锥的体积大小。
预设3:利用正方体、长方体、圆柱的高相等,只需要比较底面积,16>15>12.56,得出正方体的体积比较大。最后只需要通过计算比较正方体和圆锥的体积就可以了。
小结:看来我们在比较的时候,除了直接计算,有时还可以观察数据,然后选择合适的方法进行比较,这样就会有事半功倍的效果。
【设计意图:在有了“比表面积”的经验之后,学生在“比体积”时就可以灵活选择多种方法。练习中有等高的正方体、长方体、圆柱,也有等底的圆柱和圆锥,具体要怎么比较,学生可以自行选择。但无论是“比表面积”还是“比体积”,我们首先要肯定直接计算进行比较的这种方法,这是作为复习课“保底”的根本。然后在特定的条件下,鼓励学生灵活地选择比较的方法,将复杂的问题变成更为简单的问题,渗透转化的数学思想,使得学生在今后的学习中思路更为开阔。】
四、反思梳理,提升问题解决的能力
师:回顾这节课的学习,你有什么样的体会?又有怎样的收获?
总结:虽然这些立体图形的形状各不相同,但是它们之间是有联系的。因此在计算体积或表面积时,我们可以运用相同的公式。当然,在解决实际的问题中,我们还可以灵活地选择方法,有时并不需要“死算”,选对了方法,就能起到事半功倍的效果。
【设计意图:在课的最后,让学生自己梳理有助于学生对整节课的内容进行消化与吸收,尤其是表面积的计算,进一步统一为S=Ch+S底×2 对一些学生来说冲击还是比较大的。因此,留有时间让学生去反思,能够促进他们今后更好地学习。】
