让学生成为自主的发现者——《带余除法》余数与除数大小关系的发现教学探析

郑 慧

“让学生成为自主的发现者”，越来越成为广大教师的教学共识。但如何“让学生成为自主的发现者”则需要精心地设计和有效地实施。在一次与浙江省新思维教科院合作磨课的活动中，我执教《带余除法》一课中对“余数与除数”关系部分的教学处理尤其得到大家的认可，学生普遍能够借助操作活动，积极、自主地探知余数和除数之间的关系。经由新思维教研员的共同点评、分析，使我对驱动和支持学生自主学习有了更深的认识，以下特作整理，与广大同行分享。

【教材分析】

《带余除法》是人教版二年级下册第六单元的内容。“余数为什么比除数小”是《带余除法》一课的学习难点。人教版教材编排了用小棒摆正方形的操作活动，通过逐渐增加小棒的总根数得出一组联系且有变化的算式（除数相同，被除数和余数发生变化），进而发现余数和除数之间的关系。

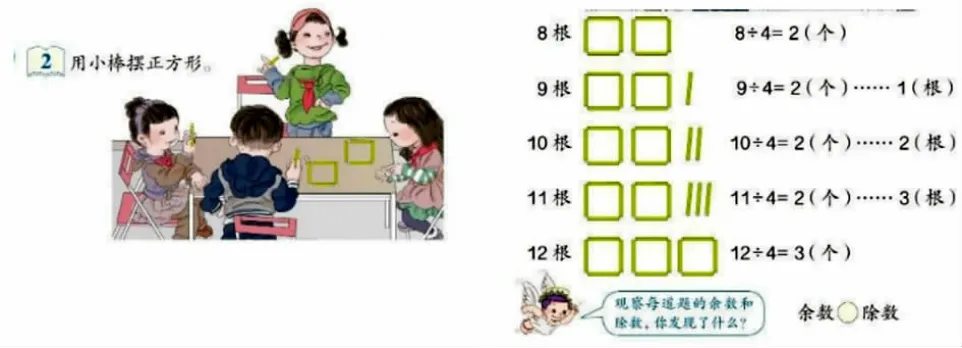
摆小棒的操作活动有其自身的优越性。首先，摆小棒有利于学生深入理解带余除法的意义。比如9÷4=2（个）……1（根），学生联系摆小棒的操作过程，能把抽象的算式和操作活动建立联系：即9 根小棒摆正方形，每个正方形需要4 根小棒，可以摆出2 个正方形，还多1 根小棒。学生结合操作不仅理解了每个算式的意义，还能对每个数所表示的实际意义作出解释，这为发现余数和除数的关系做了铺垫。其次，摆小棒的呈现过程具有结构性，凸显余数的周期性变化。左边是小棒的总根数，中间是摆正方形的结果，右边是用除法算式表示的拼摆情况。从上而下我们能清楚地看出小棒总根数的连续变化过程，直观地看到操作结果以及余数的变化情况。学生通过操作、观察、分析和比较，体会余数的产生过程、感受余数的周期性变化规律、发现余数和除数的关系。

【教学过程】

●活动一：摆正方形，可能余下几根？

1.教师展示一堆火柴棒（具体数量不明，学生只看到有很多），示范摆出两个正方形。

师：接着往下摆，如果摆到最后有剩余，你们认为会剩下几根？（学生安静地思考后进行全班交流）

生1：（犹疑地）剩下1 根。

生2：可能剩下1、2、3 根。

生3：（肯定地）最多剩下3 根。

师：为什么最多剩下3 根，而不是4 根、5 根呢？

生3：因为摆一个正方形要4 根小棒，剩下3 根摆不成正方形，剩下4 根、5 根的话可以再接着摆。

师：刚才有的说余下1 根，有的说余下1、2、3根，还有的说最多剩下3 根，那我们用小棒摆摆看。

生：那么多小棒要摆到什么时候？太麻烦了。

师：是的，全部摆完太麻烦了，我们可以从小数量开始研究。

2.每位学生用小棒摆正方形，并完成表格。

?

3.全班交流。

生：8÷4=2（个），表示用8 根小棒摆，每个正方形用4 根小棒，摆出2 个正方形。

生：9÷4=2（个）……1（根），表示用9 根小棒摆正方形，每个正方形需要4 根小棒，可以摆出2 个正方形，还多1 根小棒。

师：这两位同学说得很完整，下面同桌交流剩下几个算式的意义。

师：通过摆，你们发现剩下几根小棒？

生：只能剩下1 根、2 根、3 根。

生：剩下的小棒不可能比3 根多，比3 根多得话就可以接着摆正方形了。

师：同学们分析得很好。摆一个正方形要4 根小棒，那么余下的小棒数一定比4 根少，所以只能余下1、2、3 根。

师：继续往下摆，算式怎么写？（学生回答，教师板书算式）

师：观察余数，你有什么发现？

生：余数是有规律的，前面是1、2、3，后面又出现1、2、3。

生：余数1、2、3 一组，一组一组重复出现。

师：如果把正好分完看成余数是0，那么余数0、1、2、3 为一组，重复出现。余数确实不可能出现4。

（板书：摆正方形——只能余下1 根、2 根、3 根）

●活动二：摆三角形或五边形，最多余下几根？

师：用这些小棒摆三角形，如果有剩余，最多余下几根？想一想，有困难的同学可以摆一摆。

生：摆三角形最多余下2 根。因为摆一个三角形要3 根，所以只能余下1 根、2 根，最多剩下2 根。

师：大家同意他的说法吗？哪位同学上来摆给大家看看。

（板书：摆三角形——只能余下1 根、2 根）

师：用这些小棒摆五边形，如果有剩余，最多余下几根？

生：最多余下4 根。因为一个五边形要5 根小棒，最多余下4 根。

生：摆五边形要5 根小棒，余下1、2、3、4 根小棒都不能摆，最多余下4 根。

（板书：摆五边形——只能余下1 根、2 根、3根、4 根）

●活动三：余数和除数有什么关系？

师：通过摆正方形、三角形、五边形，你发现了余下的根数和什么有关系？

生：摆正方形，余下的根数比一个正方形需要的小棒数要少。

师：你能说得具体一些吗？

生：摆一个正方形需要4 根小棒，那么余下的根数就要比4 根少。

师：说得真有条理。谁来说一说三角形、五边形？

生：摆一个三角形要3 根小棒，那么余下的根数就比3 根少。

生：摆一个五边形要5 根小棒，那么余下的根数就比5 根少。

师：说得清楚、明白！我们可以用一句话来概括：余下的根数一定比摆一个图形所需要的根数少。

师：余下的根数是除法中的什么数？摆一个图形所需要的根数又是除法中的什么数呢？我们到这组算式中来找一找。（再次观察摆正方形的算式）

生：余下的根数就是余数。

生：余数是1、2、3，它们表示余下的根数。

师：摆一个图形所需要的根数就是除法中的什么数？

生：摆一个正方形要4 根小棒，4 就是除法中的除数。

生：这些算式中所有的除数都是4，它们都表示一个正方形所需要的小棒是4 根。

师：余数和除数之间会有怎样的关系呢？

生：余数要比除数小。

师：你是怎么想到的呢？

生：除数4 表示一个正方形的小棒数，余数表示剩下的小棒数。余下的小棒数一定比一个正方形的小棒数少，也就是说余数要比除数小。

师：他把两者之间的关系解释得很清楚。余数比除数小，也就是说余下的根数比摆出一个图形所需要的根数少。

【反思】

苏霍姆林斯基说过：在人的心灵深处都有一种根深蒂固的需要，这就是希望感到自己是一个发现者、研究者、探索者。本课中，学生在任务引领下，经历了猜想、操作、观察、比较、归纳等过程，以探究余下的根数为切入点，逐步感悟余下的根数与摆一个图形所需要根数之间的关系，最终联想到余数和除数之间的关系。

一、借助操作直观

摆小棒有两个目的：首先，结合操作，更好地理解带余除法的意义。学生联系摆小棒的操作过程，能把抽象的算式和操作活动建立联系，解释整个算式的实际意义。其次，结合操作，聚焦余数和除数的关系。余下的根数为什么只能是1、2、3，而不可能是4？这为余数和除数之间建立起联系。

而从初步感知到联系再到真正领悟最后到建立关系，又有一个递进的过程。

第一层次，通过摆正方形，得到一组联系且有变化的除法算式。学生通过操作、观察，发现摆正方形时只可能余下1、2、3 根，余数呈周期性变化。进一步，学生又发现余数产生周期性变化的原因在于小棒总根数虽然在不断增加，但小棒剩余数则每增加到4 根时又能摆成一个新的正方形，所以不可能剩下4 根。

第二层次，进一步丰富活动经验，感悟余下根数和摆一个图形所需根数之间的关系。让学生借助摆正方形中获得的初步的思维经验，思考用小棒摆三角形或五边形，最多剩下几根小棒？当摆的图形发生了变化，剩下的小棒也跟着发生变化，摆三角形最多余下2 根，摆五边形最多余下4 根。在比较中概括相同的本质的关系，即，余下的根数总是比摆一个图形所需的小棒根数要少。

最后一层，将操作情境中的数量关系抽象为带余除法中的数学关系。具体的操作活动为抽象的关系概括提供了具象的支持，学生结合操作，能在余下的根数、摆一个图形所需的小棒数和余数、除数之间建立对应关系，从而能更好地理解带余除式各部分的意义，概括出余数和除数的关系——这种概括不仅是形式上的概括，同时能解释其中的原因。

二、督促抽象思考

在操作活动中，先摆后想、先想后摆所隐含的思维含量完全不同。这里的摆，指摆正方形。想，指思考可能余下几根。

我曾尝试过先摆后想，发现先摆后想的思维含量较低。教师先让学生用小棒摆正方形并写出算式，然后观察算式说说余数的特点。在这个过程中，问题只存在于教师头脑中，学生接受的不过是一个个机械的操作指令。从而，他们汇报的也只是每次所见的现象，并没有思考现象背后的数学原理，思维停留在低层次，何谈自主、发现？

先想再摆则构建了学生自主发现的空间，提供了高层次思考的机会。出示一堆小棒，抛出一个大问题：用这堆小棒摆正方形，可能会余下几根？小棒的总根数不知道，无法计算，这给了学生一种挑战。不能动手搭，缺乏操作支撑，又增加了思考的难度。先知先觉的学生凭借原有的生活经验，想到了可能的结果，而大部分学生还似懂非懂。此时，摆小棒成了学生的内在需求。而有了问题的引领，学生在摆的时候自然而然地关注余下根数，逐步感悟到余下的根数和摆一个正方形小棒数之间的联系。在正方形直观经验的基础上，让学生思考、想象摆三角形或五边形，最多余下几根？进展到表象思考的阶段。通过所摆图形的水平变式，摆图形所余根数与所需根数之间的关系更加明朗。综合以上，形式化地概括出余数和除数的关系也就水到渠成了。

先摆再想，摆停留在“手”，更多的是执行教师的指令；先想再摆，摆是思考的“物化”部分，是学生为了解决问题，寻找的一种思维手段。