深挖教材，让课堂教学“潜入”深处

刘 瑾

在教学中教师需要思考，需要用心去处理教材，深挖教材。深挖教材挖什么呢？挖教材的教学目标——即教给学生什么？挖教材中的重点、难点——即要怎么教才行？挖教材的生长点——即要培养学生的什么能力素养？这是教师每节课都要考虑的几个基本点。只要教师坚持去做，久而久之肯定会越“挖”越深，越“挖”越有思考，在不断的思考中让课堂“潜入”深处。

一、挖教学目标

在上每一节课之前，教师首先要研读教学目标，根据教学目标来思考自己的教学设计。教学目标也要分轻重缓急，有些教学目标可以在后面慢慢渗透，但是有些目标必须及时有效地让学生感悟到一定的高度，拖不得、缓不得。

比如《三角形》这个单元，它的教学目标有很多，比如进一步认识三角形，建立三角形的概念，理解三角形的定义；在动手操作、思辨的过程中形成三角形的表象；理解三角形的特性，知道三角形高的含义，会在三角形内画高，能认识三角形的三条高；在动手操作的过程中体会三角形的稳定性，了解其在生活中的运用；在动手操作的过程中掌握三角形的三边关系等等。

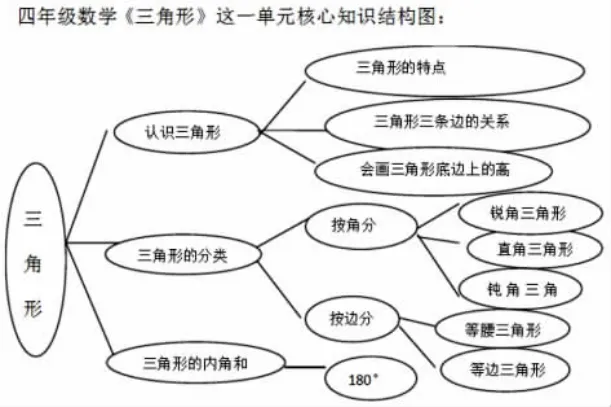
这些目标都很重要，但是我觉得有些目标需要一步到位，让学生进行充分的体会和感悟，如果当时没有学到位，就会变成“夹生饭”。我觉得这个单元中需要挖掘的目标：一个是建立三角形的概念，在思辨的过程中形成三角形的表象；另一个是在动手操作、猜测、验证的过程中掌握三角形的三边关系，并在以上的目标中培养学生相关的数学素养，比如猜测验证的能力，动手操作的能力等等。根据以上的目标定位，我们再去设计教学，在教学中可以有意识地放大这些目标，让学生有充分的时间去感悟、去理解。

再比如三下《面积》这个单元，要达到的教学目标也有很多，如感受面积的含义，理解什么是面积，体会用合适的面积来测量面积的重要性；在动手操作和观察中感受面积单位的大小，认识三个常用面积单位等等。

这么多教学目标中，我认为最需要挖掘的首先是面积的含义，感悟到底什么是面积，让学生从一维的空间观上升到二维的空间观，为后续面积的计算教学做好铺垫。其次是把面积测量的教学纳入到测量教学的大环境中，为了知道线段的长度，我们用线来测量线。为了知道某个角的度数，我们用角来测量角。只不过我们事先规定了多长的线段是1 厘米、1 分米、1 米，规定了多大的角度是1 度而已。那么我们在测量面积大小时或者在比较面积大小时，我们又要用什么去测量面积大小呢？当然是用面测面，只是学生还没有意识到用哪种面去测量比较好。在学生一开始接触到面积大小的比较或者测量时，我们就要让学生去操作和感悟到底哪种面可以进行比较精准的测量。在这一过程中体会到面积的本质含义，面积就是由一个个的小面累铺而成的，并在这一过程中感悟到用正方形作面积单位的合理性。另一个重要的教学目标便是长方形和正方形面积的计算，这是为以后继续学习面积和体积做基础的。在前面教学目标的引领下，这里的面积教学也应该很顺利，因为对于面积的观念已经通过教学深入学生内心了。

二、挖重点难点

教学重点一定是一节课中的重中之重。在一节课中，如果新旧知识都有，那么新知识是这节课的重点；在一节课中如果全都是新知识，则应按其地位分出主次，确定重中之重；在一节课中如果全是旧知识，那么这些旧知识的综合运用就是这节课的重点。

教学难点是学生学习的困难点、困惑点。因此，教学难点应该根据学生的学习情况来决定，难点的确定既要分析教材，又要分析学生，所以难点一般出现在以下几个方面：一是新知识超出了学生已有知识的范围；二是新知识与学生固有的定向思维不一致；三是新知识与原有的旧知识有很大的距离。

在教学中突出重点、突破难点，要体现在环节安排、教法选择、时间分配等各个方面。若重点难点是包含和同等关系时，可以统一安排；若是并列关系则应分别安排。教材中往往是多种情况综合在一起，因此教学中一定要具体情况具体分析，采取与教材相适应的方法，突出重点、突破难点。

比如《三角形的认识》这节课，大部分学生知道怎样的图形是三角形，把几个跟三角形相像的图形摆在三角形之中，学生一定能选出正确的三角形，但是也有可能选出像三角形而不是三角形的图形。针对这样的情况，我们确定的教学重点是：在操作和辨析的过程中形成三角形的表象，建立三角形的概念，理解三角形的定义。于是我们设计了这样的环节，放手让学生去进行辨析，首先确定哪些是三角形？其余的为什么不是三角形？在这样的教学设计下，学生一定能够感悟到三角形的本质含义，到底怎样的图形才是三角形。

三、挖教材的生长点

何为生长点？顾名思义就是师生一起通过教学材料的学习，在原有的知识脉络上又新生出一些知识，这些知识需要教师就某一知识点进行深入挖掘，使之成为新知识的生长点，或成为某几个知识点的连接点，从而使学生所学的知识融会贯通，最终达到培养学生创造能力的目的。

每节课都有新的知识产生，但是有些知识的增长，需要教师有一种意识，即这个知识点将要为哪个知识点进行服务，或将要与哪些知识进行沟通融合，然后我们就要往那个方向进行教学。

教师在教某一节课时，要想到学生后面将要学习的好几节课。要知道每一节课都不是独立而生的，某节课的知识点都是与下一节课、下下节课的知识点相关联的。知识之间是呈链条结构环环相扣、节节相连的，知识之间是旧里蕴新，又化新为旧的。如果我们在教学中让某一个知识孤立起来，那么在以后的综合性实际应用中就会问题凸显，让学生没法与其他知识进行沟通理解，使学习变得困难。

比如在《三角形三边关系》这节课中，我们可以在学生掌握了三角形的三边关系之后，设计这样一个教学过程，让学生试着改变其中一组不能围成三角形的数据，比如18 厘米、6 厘米、2 厘米，让学生改变2 厘米这条线段，提问学生：如果规定都是整厘米数，2 厘米这条边可以改成哪些厘米数？在学生整理得出所有情况后，教师提问：24 可以吗？24+6＞18，不是可以吗？在学生思辨的过程中让学生感悟体会，在这种情况下，较长边已经不是18 厘米这条边了，也就是说较短的两条边发生了变化。这样的体验，让学生经历思维的冲突，达到破除思维惯性，让学生带着思考去观察分析数据的目的，为以后三角形的继续学习打好基础。

又比如在学习了2、3、5 的倍数之后，设计了一节拓展性的课《9 的倍数的特征》，因为有了前面学习2、3、5 倍数特征时知识方法的迁移，所以学习《9 的倍数的特征》这节课，对于学生来说并不难，学生通过几个数据的尝试就能很快地得出9 的倍数的特征，在研究的过程中让他们体会到了知识之间的联系。但在这一节课上，我们着重要挖掘的知识增长点是什么呢？学生已经学了那么多数的倍数特征，那么是什么原因使得只要各个数位上数字的和是9 的倍数，这个数就是9 的倍数呢？通过学生的猜测、推理、验证，得到了关于一个数的倍数特征的一般关系式（如下图），让学生在头脑中对多个知识点之间进行沟通联系，同时也学会了学习知识的一般方法，并把知识的学习引向了远处，其他数的倍数特征又将是怎样的呢？你能够通过这个关系式来加以说明吗？

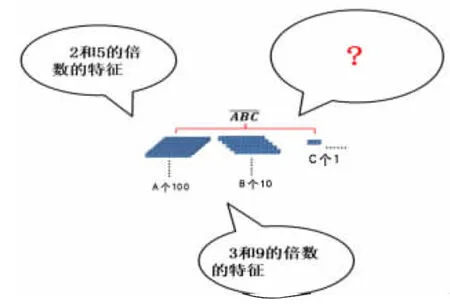
这样就给学生留下一个强烈的印象，对待以后的学习需要一丝不苟地去钻研，会多问自己几个为什么。

总之，在教学中我们要深挖目标，分析知识中的重点、难点，找准知识的生长点，在遵循学生认知规律和认知经验的基础上，充分挖掘教材，让我们的课堂更深入，让知识在学生的头脑中形成脉络，达到培养学生素养和持续发展的目的。