单晶金刚石磨粒机械磨损声发射关联维特征研究

吴海勇

(1.漳州职业技术学院机械工程学院，漳州 363000；2.华侨大学制造工程研究院，厦门 361021；3.福建龙溪轴承(集团)股份有限公司博士后科研工作站，漳州 363000)

1 引 言

单晶金刚石广泛应用于磨粒加工领域[1]。单晶金刚石磨粒加工过程中的磨损受到实际工况的影响，其磨损形式大多表现为机械磨损、化学磨损和热磨损等三大类[2-4]。其中，机械磨损是单晶金刚石磨粒的主要磨损形式之一，是金刚石磨粒与工件、切屑在切削、冲击、挤压和摩擦等一系列复杂物理过程中产生的。单晶金刚石磨粒的机械磨损是导致其失效的主要形式之一，学者通过加工过程中磨粒表面形貌[5]、切削力[6]、声发射[7]等物理参量对其机械磨损进行综合表征和评价。其中，利用声发射技术监测金刚石磨粒加工过程中内部微小结构尺寸变化以及弹性波释放现象[8-9]，是表征和评价金刚石磨粒的机械磨损特性重要方法之一。由于单晶金刚石磨粒工具加工过程中存在着磨粒之间的相互干涉，以及切削液、切削热等的影响，加工工况的复杂性导致了磨粒的磨损形式较为复杂[10]。因此，利用单颗单晶金刚石磨粒划擦加工工件是研究其纯机械磨损的主要方法之一。利用声发射技术研究单颗金刚石磨粒划擦过程中的机械磨损特性，可以选择的工件对象较多，其中高温合金Ta12W是一种较为合适的材料。这主要是由于Ta12W具有良好的耐磨性和耐高温性，与金刚石的亲和性差[11]，学者研究表明金刚石磨粒加工Ta12W过程中主要以机械磨损形式表现出来[12-14]。从以往的研究中可以发现，单晶金刚石磨粒划擦Ta12W的机械磨损随着划擦时间的变化呈现非线性变化特征，磨损声发射信号受到多方面因素的综合影响，是时间的函数，属于非线性时间序列动力系统，存在着确定性的一面和随机性的一面。利用关联维数对非线性时间序列动力系统进行识别和表征是一种行之有效的手段。关联维数对动力学系统的非线性、非平稳性敏感程度较高，可较好反映出动力学系统信号的非线性固有规律，关联维法分析广泛应用于刀具的磨损监测[15]以及机械故障[16]的诊断中，而对于单晶金刚石磨粒机械磨损声发射信号的关联维特征却尚不明晰。

本文利用声发射技术监测跟踪单颗单晶金刚石磨粒划擦Ta12W过程中的机械磨损特性，分析金刚石磨粒机械磨损声发射信号特征，利用基于G-P算法计算磨粒机械磨损声发射信号关联维数特征，旨在进一步揭示单晶金刚石磨粒的机械磨损特性。

2 试 验

2.1 试验条件

图1 试验装置示意图( a)装置示意图;(b)试验装置图 Fig.1 Schematic diagram of experimental setup (a)schematic diagram;(b)experimental setup diagram

利用精密平面磨床Planomat HP408进行单颗单晶金刚石磨粒的机械磨损测试试验，如图1所示。单颗单晶金刚石磨粒钎焊粘结到铝盘基体上，工件紧密粘接到安装在测力仪的夹具板上。金刚石磨粒以槽磨形式划擦工件，划擦速度为20 m/s，进给速度为0.6 m/min，划擦深度10 μm。试验过程中无使用冷却液。槽磨每间隔一段固定长度(20 mm)后，对金刚石磨粒的机械磨损特性(形貌、磨损体积等)进行检测分析，直至磨粒完全磨损。

表1 Ta12W的物理机械性能Table 1 Physical and mechanical properties of Ta12W

Ta12W工件的物理机械性能见表1，工件表面粗糙度Ra为0.377 μm，试验使用元素六Element Six SDB1125品级、平均粒径约为0.725 mm的单晶金刚石磨粒。

2.2 检测与分析

在单晶金刚石磨粒的每个划擦间隔阶段，利用德国蔡司激光共聚焦显微镜LSM700测量其磨损体积以及台式扫描电镜FEI Phenom prox检测其磨损表面形貌。利用美国物理声学数字声发射检测仪(Physical Acoustics Micro-Ⅱtype)监测单晶金刚石磨粒机械磨损过程声发射信号，声发射传感器为ISR15/AB64，声发射信号通过20 dB的前置放大器进行放大后由PCI2采集系统进行采集，具体参数为：采样频率10 MHz，采样带宽1 kHz～1 MHz，采样长度为15 k，门槛电压为55 dB，浮动门宽6 dB。

3 结果与讨论

3.1 金刚石磨粒的机械磨损

单晶金刚石磨粒在划擦过程中表面形貌和磨损体积的变化历程如图2所示。从金刚石磨粒的磨损体积Qd和工件材料去除体积Qw的变化趋势可知，磨粒的机械磨损可以分为初期磨损、稳定磨损和剧烈磨损等三个阶段。磨粒的机械磨损从切削刃接触弧区逐渐扩大到磨粒顶部{100}晶面，在稳定磨损期磨粒的局部磨损区域缓慢扩大；在剧烈磨损阶段，金刚石磨粒出现了大面积的解理磨损，之后磨粒的机械磨损速率加快，磨粒内部出现较大的裂纹，磨粒出露部分基本脱离钎焊基面，磨粒完全磨损。另外，磨损体积变化曲线的斜率即为磨损率，则可计算得到初期、稳定和剧烈磨损的磨损率ε分别达到了0.341、0.241和0.281。

3.2 声发射信号特征

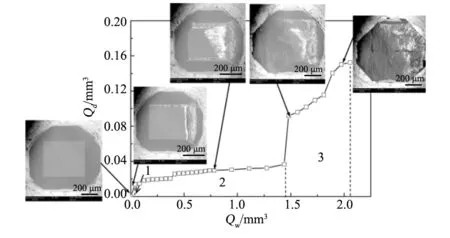
图2 单晶金刚石磨粒机械磨损变化历程 Fig.2 Mechanical wear progression of the single crystal diamond grit

单颗单晶金刚石磨粒在每次旋转划擦工件过程中均会产生一次磨损声发射信号。声发射信号的特征参数表征其信号特性的方式之一，统计金刚石磨粒在三个不同磨损阶段中声发射特征参数值的平均值进行分析，如表2所示。可见，金刚石磨粒在划擦过程中，随着其机械磨损程度的加剧，声发射信号的计数值、能量、幅值和有效电压均方根RMS等特征参数均有不同程度的增加，其中能量和RMS的增加幅值较大，尤其在磨粒剧烈磨损阶段更是得到了大幅度增加。磨粒机械磨损的加剧，使声发射信号特征参数快速增加。

表2 单晶金刚石磨粒机械磨损的声发射特征参数Table 2 AE characteristic parameters of the mechanical wear for single diamond grit

每次声发射撞击信号采样间隔为0.1 μs，采样信号点数为15360个，选取单晶金刚石磨粒在不同机械磨损阶段的典型单次声发射时域信号进行分析，如图3所示。金刚石磨粒在初期(图3a：Qw=0.0411 mm3)、稳定(图3b：Qw=1.479 mm3)和剧烈磨损(图3c：Qw=2.055 mm3)阶段的声发射信号最大振幅分别达到了290 dB、320 dB及2200 dB，可见，剧烈磨损阶段声发射信号幅值远大于前两阶段的变化幅值。

3.3 磨损关联维分析

3.3.1 关联维G-P算法

G-P算法是Grassberger和Procaccia在坐标延迟相空间重构和嵌入定理基础上，推导得到的一种关于混沌吸引子关联维数的计算方法[17]。对于单晶金刚石磨粒划擦Ta12W过程中，其机械磨损声发射信号时间序列{xi,i=1,2,3…N}，通过合理的计算嵌入合适维数m和时间延迟τ后，可对该一维声发射信号进行相空间的重构，得到重构相空间的轨迹矩阵：

X1=[x1,x1+τ,…x1+(m-1)τ]T,X2=[x2,x2+τ,…x2+(m-1)τ]T,…Xi=[x1,x1+τ,…xi+(m-1)τ]T

(1)

式中N=n-(m-1)τ，n为磨损声发射时间序列信号点数。在金刚石磨粒机械磨损的非线性变化过程中，影响磨损的各个状态变量是相互作用的，其中一个状态变量的变化将会影响到其他变量，在磨粒划擦机械磨损的全过程中，磨损声发射时间序列中包含了参与此变化系统的其他影响变量的有关信息。在磨损声发射数据足够且排除噪声干扰的情况下，通过确定合适的嵌入维数m和时间延迟τ，可以实现由部分把握整体[18]。

图3 金刚石磨粒不同磨损阶段声发射时域信号：(a)初期磨损(Qw=0.0411 mm3); (b)稳定磨损(Qw=1.479 mm3);(c)剧烈磨损(Qw=2.055 mm3) Fig.3 AE time-domain signal of diamond grit in different wear stages(a) initial wear stage (Qw=0.0411 mm3); (b) steady wear stage (Qw=1.479 mm3);(c) acute wear stage (Qw=2.055 mm3).

单晶金刚石磨粒机械磨损声发射信号关联函数C(r)可以定义为：

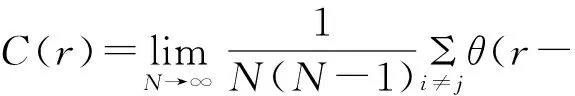
(2)

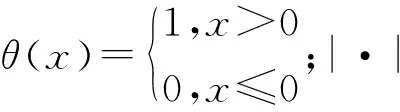
(3)

因此，要分析单晶金刚石磨粒机械磨损声发射信号关联维特征，可通过对信号相空间进行重构并计算得到其双对数曲线关系(即lnC(τ)-lnτ)，计算该双对数曲线中相对较长一段近似直线部分(即无标度区间)的斜率即为其关联维数D。

3.3.2 时间延迟的确定

单晶金刚石磨粒机械磨损声发射信号相空间中状态矢量Xi和其他矢量之间时彼此独立或不相关，每个分量代表了相空间中独立的点坐标，时间延迟的确定主要是取决于以下几点因素：(1)时延是试验采样时间间隔的倍数；(2)若时延过短，导致状态矢量Xi和Xi+r之间的独立性不足，使相空间轨迹趋向同一位置，信息特征难以显露；(3)若时延过长，由于试验测量误差的干扰，使矢量Xi和Xi+r之间丧失动力学联系[19]。信号重构相空间时间延迟的确定主要有自相关函数法或平均互信息法等[20]。本文采用自相关函数法确定金刚石磨粒机械磨损声发射信号相空间的时延，信号自相关函数R(τ)的定义如下式：

(4)

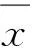
3.3.3 关联维数分析

图4 不同磨损声发射自相关函数R(τ)与时延τ的关系 Fig.4 Relationship of the autocorrelation function R(τ) and time delay τ for AE signals in different wear stages

利用式(2)计算单晶金刚石磨粒机械磨损声发射信号相空间关联积分，与测度r的选取密切相关，测度r的取值应小于磨损声发射信号系统吸引子在m维空间的最大伸展距离dmax。若r过大，则C(r)=1，导致磨损声发射有用信号被淹没；若r过小，则C(r)=0，使得声发射噪声信号突出干扰有用信号。测度r的选择包含了声发射信号相空间中的整个无标度区间，为保证计算结果的可靠性，本文利用等指数比例递增取值法增大了分析中的计算量，算法中指数幂依等差序列递增，即r1=ea1，r2=ea2，…rn=ean，an=a1+(n-1)d，d为公差。

利用所确定的时间延迟τ，基于G-P算法可计算得到单晶金刚石磨粒三个不同磨损阶段典型声发射信号在不同嵌入维数下的双对数lnC(r)-lnr图，如图5所示。图中三种不同磨损阶段声发射信号的嵌入维数从1增加到13的双对数图，从图中可见，对于三种不同磨损阶段声发射信号而言，随着嵌入维数m的增加，双对数图的斜率逐渐收敛于一个饱和值，则可通过该近似直线部分(即相空间中的无标度区间)，计算得到该种状态下的关联维数。另外，从图中还可以发现，初期磨损和稳定磨损的双对数图变化趋势较为相似，呈现阶段性增长变化最后趋于饱和状态，而剧烈磨损阶段的双对数图则呈缓慢增长趋势最后才达到饱和值。并且地，对于相同的lnr，初期和稳定磨损阶段的lnC(r)取值远大于剧烈磨损阶段的lnC(r)值。这些差异化的变化特征直接体现在了其关联维数特征上。

图5 不同磨损阶段声发射的双对数lnC(r)-lnr图 (a)初期磨损lnC(r)-lnr(Qw=0.0411 mm3); (b)稳定磨损lnC(r)-lnr(Qw=1.479 mm3);(c)剧烈磨损lnC(r)-lnr(Qw=2.055 mm3) Fig.5 Double logarithmic lnC(r)-lnr for AE signals in different wear stages (a)initial wear:lnC(r)-lnr(Qw=0.0411 mm3); (b)steady wear:lnC(r)-lnr(Qw=1.479 mm3);(c)acute wear:lnC(r)-lnr(Qw=2.055 mm3)

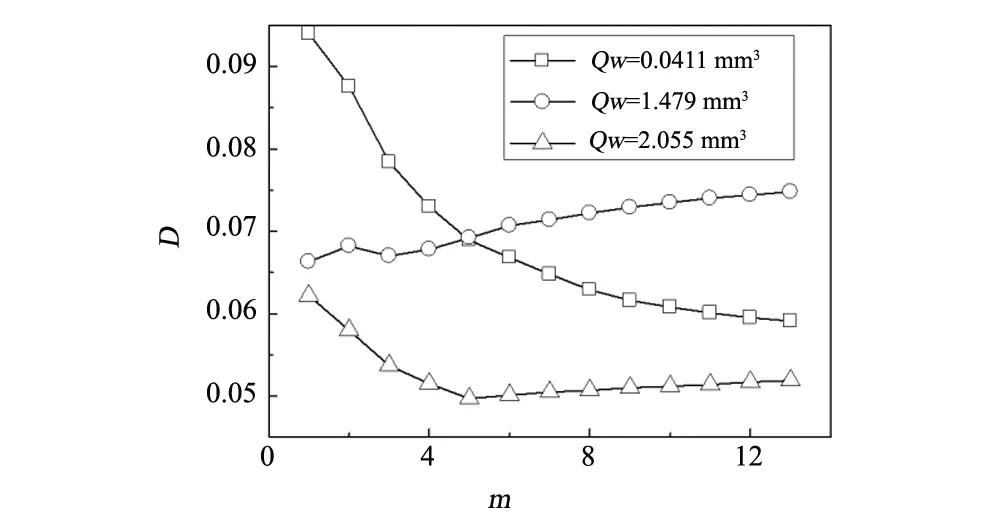
图6 不同磨损阶段声发射的关联维数 Fig.6 Correlation dimension of the AE signals in different wear stages

通过双对数图可计算得到单晶金刚石磨粒不同磨损阶段声发射信号在不同嵌入维数m时的关联维数D，如图6所示。从图中可以看出：(1)三种不同磨损阶段声发射信号的关联维数D在0.0497～0.0940之间波动变化，关联维数D属于大于零的正分数。根据文献[19-20]，若关联维数D=0，系统为定常运动；D=1，系统属于周期振动状态；D=2或3，则系统属于准周期振动；D为大于零的正分数时，系统为混沌运动；D趋于无穷大时，系统属于随机运动状态。可知，单晶金刚石磨粒划擦Ta12W的机械磨损过程属于混沌运动变化状态；(2)三种不同磨损阶段声发射信号的关联维数随着嵌入维数m的增加，关联维数D的变化趋于平稳，初期、稳定和剧烈磨损阶段的关联维数分别趋近于0.0591、0.0748和0.0519；(3)结合图2金刚石磨粒磨损体积变化趋势与关联维数D的变化趋势可见，在金刚石磨粒磨损率ε较大的区间(初期和剧烈磨损磨损率ε分别为0.341和0.282)，其关联维数D的变化幅值相应也较大(初期和剧烈磨损阶段的变化幅值分别为0.0940-0.0591=0.0349和0.0622-0.0519=0.0103)；而在稳定磨损阶段磨损体积变化较为平稳(磨损率ε为0.241)，其关联维数D的变化幅值(0.0748-0.0663=0.0085)也相应较小。因此，可见金刚石磨粒机械磨损的关联维数D变化幅值与其磨损率ε基本呈正效应关系。

4 结 论

(1)单晶金刚石磨粒划擦Ta12W的机械磨损声发射信号具有混沌运动变化特征。

(2)随着嵌入维数的增加，单晶金刚石磨粒机械磨损声发射信号的关联维数值的变化趋于平稳。

(3)单晶金刚石磨粒划擦Ta12W的机械磨损声发射信号关联维数变化幅值与其磨损率基本呈正效应关系。