地面条件下分离结晶生长CdZnTe晶体的稳定性控制

李 震 ，张全壮

(重庆市节能技术服务中心，重庆 400044)

1 引 言

分离结晶是近三十年来才发现的一种先进晶体生长技术，最近几年该领域的研究才得到飞快的发展，逐渐被重视。该晶体生长技术融合了传统的CZ法和Bridgman法的优点，在生长过程中晶体与坩埚壁之间维持一个狭小的气缝，阻断晶体与坩埚壁的接触，这样就极好地解决传统晶体生长方法在热敏感性晶体材料(CdZnTe、CdTe等)上的短板，如：传统晶体生长技术产生的晶体内部断层、位错、单晶机械强度降低等瑕疵。晶体分离生长现象最早是在1974年在美国宇航局试验卫星上发现的，在完成微重力条件下的Bridgman法晶体生长实验后，发现有部分处于坩埚壁面的晶体发生了分离结晶现象，不仅表面光滑，而且物理性能明显提升，很大程度的提高了晶体质量[1-3]。后来，Eustathopoulos等[4]对分离结晶技术进行深入研究后，认为该技术为目前生长热敏感性晶体材料的最佳方法，为后续的晶体质量提高提供了一个明确的方向。同时指出，分离结晶晶体生长技术的关键在于在熔体-晶体-坩埚壁之间获得一个稳定的气液界面。

目前，分离结晶技术在微重力条件下获得了实验成功，而在地面重力条件下一直未能取得较好的效果。其根本原因在于微重力条件下，气液界面的影响因素简单，仅仅与冷热两端的气压差、结晶生长角和接触角有关。Epure[5-6]经过理论推导，分别给出了微重力条件下相关影响因素对气液界面形状和气缝宽度的影响规律；伍顺发[7]对气液界面稳定存在的条件进行了利雅普洛夫分析，得到了有利于气液界面稳定存在的条件。由于重力的影响，地面条件下分离结晶过程中熔体液柱高度产生的静压力使气液界面形状及稳定性变得非常复杂。因此，对地面条件下分离结晶过程中气液界面形状及其稳定性的研究成为了地面分离结晶取得成功的关键，能够为地面分离结晶提供理论支持。

2 物理数学模型

图1为分离结晶技术示意图。坩埚热端(顶部)和冷端(底部)都将维持一定的气压，在熔体气液界面上会形成一个气压差，调节气液界面两侧的气压差能保证气液界面的稳定存在，开始分离结晶晶体生长。分离结晶模型关于坩埚中心轴线对称，可以选取任意垂直剖面的进行讨论。为了简化模型，在讨论过程中忽略传热和对流等因素对熔体气液界面形状影响，并假设温度变化不影响熔体-坩埚间的接触角。h为未结晶熔体的高度，ro为坩埚的半径，e为结晶过程中的气缝宽度；Ph和Pc分别表示坩埚的热端和冷端气体压力大小，M为熔体气液界面上的任意点，R1是通过M点的平面切气液界面所得到的曲率圆曲率半径，R2是通过M点垂直方向的平面与气液界面相交得到曲率圆的曲率半径；αe、θc和βc分别为结晶生长角、接触角以及M点处切线与垂直方向的夹角，s为弧线弧长。

图1 分离结晶技术示意图 Fig.1 Schematic diagram of detached solidification technology

在气液界面M点处建立力学平衡。

(1)由几何关系：

dr=dssinβc

(1a)

dz=dscosβc

(1b)

(2)由M点处曲率半径：

R1=-ds/dβc

(2a)

R2=r/cosβc

(2b)

(3)由M点处气液界面Young-Laplace力学平衡方程：

(3)

其中：

(4)

式中，b为熔体上自由表面的曲率半径，γ为熔体表面张力，M点处气液界面受到熔体的静压力大小为ρg(h-z)。

由(1)、(2)、(3)式可以导出气液界面形状的非线性微分方程组：

(5)

(6)

边界条件为：

当βc=αe时，

z=0

(7)

当βc=π-θe时，

r=r0

(8)

采用四阶龙格-库塔法编制Matlab语言程序对以上微分方程组进行求解，可以得到满足精度的数值解，大量数值解通过描点，可以描绘出地面分离结晶气液界面形状的变化过程。本文选用CdZnTe为计算工质，其相关物理参数如表1所示[8]。

表1 CdZnTe材料的物理参数Table 1 Parameters of CdZnTe

3 结果与讨论

大量研究表明气液界面两侧的压差和熔体-坩埚接触角是影响气液界面形状和气缝宽度的主要因素，由于在αc+θc<180°和αc+θc>180°时气液界面表现的形状完全不同，本文将αe+θc<180°和αc+θc>180°两种情况分别讨论。

3.1 αe+θc<180°时气液界面形状及影响因素

CdZnTe晶体材料的结晶生长角为20°，当选用SiO2材料的坩埚进行分离结晶时，熔体-坩埚接触角约为117°，而采用P-C坩埚时，熔体-坩埚接触角约为126°，此时生长角和接触角之和均满足αe+θc<180°。选用SiO2坩埚(θc=117°)在不同压差下分离结晶生长CdZnTe晶体时气液界面形状如图2所示，分离结晶过程中晶体-熔体-坩埚间的气液界面为一条向上凸起的弯液弧线(凸向熔体侧)。气液界面两侧压差增大，弧线的曲率半径逐渐减小，晶体-坩埚间的气缝宽度和气液界面的高度都减小。由此，在αe+θc<180°时，维持气液界面两侧压差较小，能够获得更大的气缝宽度，更有利于分离结晶现象的发生。

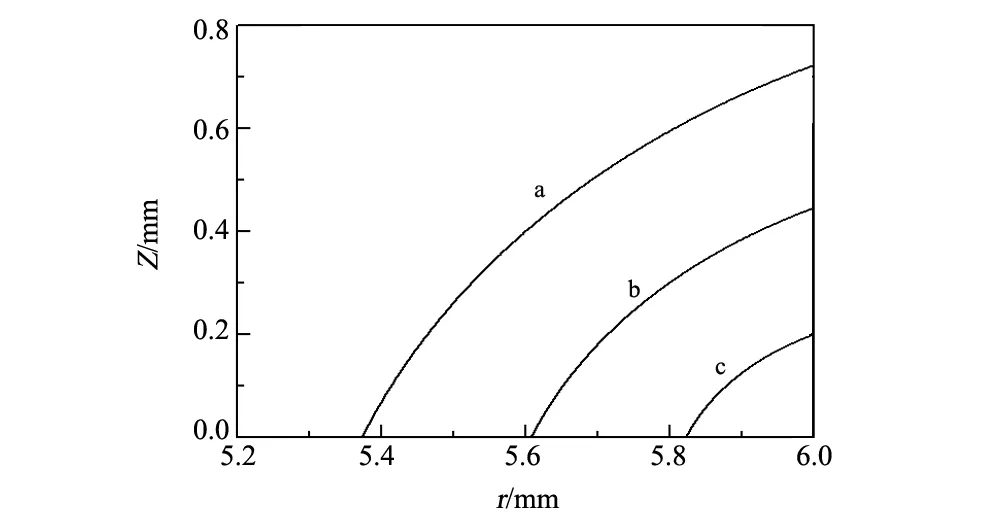
图2 θc=117°时气液界面形状 Fig.2 Meniscus shapes for θc=117°,(a)ΔPm=100 Pa,(b)ΔPm=200 Pa,(c)ΔPm=500 Pa

图3 ΔPm=200 Pa时气液界面形状 Fig.3 Meniscus shapes for ΔPm=200 Pa,(a)θc=117°,(b)θc=126°,(c)θc=135°

图3给出了ΔPm=200 Pa时，熔体-坩埚接触角分别为θc=117°、θc=126°和θc=135°时的气液界面形状(不同坩埚材料)。可以看出，熔体-坩埚接触角对气液界面形状和气缝宽度的影响较大，当θc=117°时，气缝宽度约为400 μm，而在熔体-坩埚接触角θc=135°时气缝宽度减小到120 μm以下。此时，气液界面形状发生了显著的变化，气液界面所在的弯液弧变得更加陡峭，气液界面高度以及气缝宽度明显减小，且气液界面高度减小的幅度小于气缝宽度减小的幅度。

图4描述了不同熔体-坩埚接触角时，分离结晶制备CdZnTe晶体气缝宽度随气液界面两侧压差的变化。当气液界面两侧压差ΔPm>0时，出现晶体与坩埚的分离，随着气液界面两侧压差和熔体-坩埚接触角的增大，气缝宽度不断减小。在气液界面两侧压差很小时，气缝宽度能够达到1～2 mm，但随着压差的增大，气缝会急剧减小，当气液界面两侧的压差增大到500 Pa以上时，气缝宽度减小到了几十甚至几微米的范围；另一方面，压差条件相同时，增大接触角也会减小气缝宽度，但接触角对气缝宽度的影响远小于压差的影响。由此可知，接触角主要影响气液界面的形状，而气液界面两侧压差主要影响气缝宽度。

图4 αc+θc<180°时气缝宽度与冷热端压差的变化关系 Fig.4 Function of gas-gap width as meniscus pressure difference for αc+θc<180°(a)θc=117°,(b)θc=126°,(c)θc=135°

图5 θc=165°时气液界面形状 Fig.5 Meniscus shapes for θc=165°(a)ΔPm=-100 Pa,(b)ΔPm=-200 Pa,(c)ΔPm=-500 Pa

3.2 αc+θc>180°时气液界面形状及影响因素

CdZnTe熔体与大多数坩埚的都只能满足αc+θc<180°，很难达到αc+θc>180°的条件。在坩埚表面涂覆一层其它材料(如：硼氮化合物、碳纤维等)，熔体-坩埚接触角显著增大，使αc+θc>180°的条件成为可能。而αe+θc<180°时熔体气液界面的存在并不稳定，只是处于一种亚稳定状态[9]，该状态表现为仅仅是一个相对的稳定，会随着时间的变化(即使没有任何扰动)，或者是受到细微外界扰动时，晶体会与坩埚壁面重新黏附而中断分离结晶，这正是地面分离结晶难以实现的关键所在。而αc+θc>180°时，当受到外界扰动时，晶体生长系统能保持自身稳定，衰减外界扰动对系统的影响，实现稳定的分离结晶。

图5给出的是θc=165°时压差分别为ΔPm=-100 Pa、ΔPm=-200 Pa和ΔPm=-500 Pa时的气液界面形状。αe+θc>180°时控制气液界面两侧出现较小的负压差(ΔPm<0)更有利于实现分离结晶，此时气液界面的形状发生了明显变化(与αe+θc<180°时相比较)，气液界面所在的弯液面弧线由凸向熔体侧转变成了凸向气侧。

ΔPm=-200 Pa时，不同熔体-坩埚接触角条件下气液界面形状分布如图6所示，熔体-坩埚接触角发生变化时，气液界面形状发生了明显的变化，随着接触角的减小气液界面变得更加平缓，气缝宽度随着接触角的减小而减小。因此，αc+θc>180°时，较大的接触角更有利于维持稳定的分离结晶。

图6 ΔPm=-200Pa时气液界面形状 Fig.6 Meniscus shapes for ΔPm=-200 Pa (a)θc=168°,(b)θc=165°,(c)θc=163°

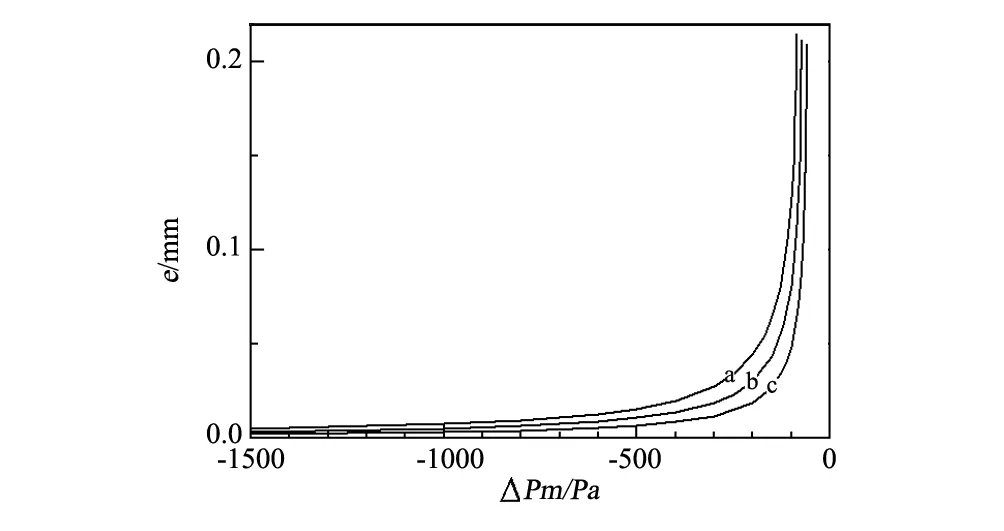
图7 αc+θc>180°时气缝宽度与气液界面两侧压差的变化关系 Fig.7 Function of gas-gap width as meniscus pressure difference for αc+θc>180°(a)θc=168°,(b)θc=165°,(c)θc=163°

图7给出了气缝宽度受气液界面两侧压差以及熔体-坩埚接触角的影响情况，气缝宽度随气液界面两侧负压差的减小而增大，随熔体-坩埚接触角的减小而减小。当气液界面两侧的负压差较小时，气缝宽度能达到几百微米，当负压差增大到-500 Pa以上时，气缝宽度仅仅只有十几微米甚至是几微米，很容易导致熔体与坩埚重新黏附，无法完成分离结晶。因此，在分离结晶晶体生长过程中应尽量控制气液界面两侧负压差较小，这样更有利于分离结晶。

3.3 数值结果的回归分析与讨论

分离结晶是否实现对压差要求非常苛刻，为了实现稳定的分离结晶，最好能够实现压差的自动控制调节，给出气缝宽度受各因素影响的关系式具有非常重要的意义。αc+θc<180°时，分离结晶过程处于亚稳定状态，给出其经验关系式意义不大。而当αc+θc>180°时，能够形成稳定的分离结晶过程，对大量数值计算结果的进行线性回归分析，拟合出对应的关系式如下：

(12)

其中，A=0.2736cos(αe+θc)+0.2725，N=5.382cosθc+4.360，αe+θc>180°

为检验拟合关系式的正确性及误差大小，将拟合值与数值计算值在同一坐标下的对比如图8所示，拟合值与数值计算值的偏差在±25%以内，而且正负偏差以零偏差线为中心轴的轴对称分布，基本符合拟合要求。

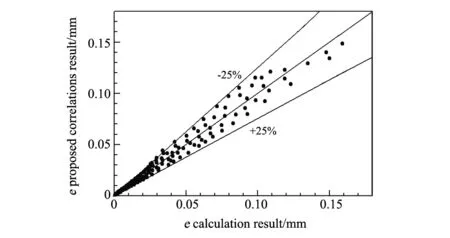
图8 气缝宽度数值计算值与拟合值的比较 Fig.8 Comparison of the numerical calculation results with the proposed correlations of the gap's width

3.4 稳定分离结晶的压差控制

随着结晶过程的进行，熔体液柱高度不断减小，气液界面静压力也会随之减小。因此，分离结晶过程中需要通过压差控制器调节熔体冷热两端的气压差，以维持气液界面两侧的压差稳定，达到实现地面稳定分离结晶的目的。

晶体材料的结晶生长角和熔体-坩埚接触角不会随着结晶过程(时间推移)而变化，则有：

(13)

(14)

这里，ΔPm=Pc-Ph-ρgh，引入结晶速度Vg,有：

(15)

结合(14)、(15)两式容易得到：

(16)

由此得到维持稳定的分离结晶的必要条件为熔体冷热端气压差的调节速率与结晶速率成线性变化。

4 结 论

本文建立了地面分离结晶控制气液界面形状的Young-Laplace力学平衡微分方程组，采用四阶龙格-库塔法得到地面分离结晶气液界面形状，讨论了气液界面形状和气缝宽度的影响因素和规律，给出了稳定分离结晶的压差控制条件。结果表明：

(1)气液界面两侧压差和熔体-坩埚接触角是影响分离结晶气液界面形状和气缝宽度的关键因素。

(2)当αc+θc<180°时，气液界面为一条凸向熔体侧的弯液弧，气缝宽度随着气液界面两侧压差的增大而减小，随着接触角的增大而减小。

(3)当αc+θc>180°时，气液界面为一条凸向气侧的弯液弧，气缝宽度随着气液界面两侧负压差的减小而增大，随着接触角的增大而增大。

(4)当熔体冷热端气压差变化与结晶速率呈线性关系时，气缝宽度能够维持不变，实现稳定的分离结晶。