一类平面数字限制集的维数
2022-12-01董家梅席玉佩
董家梅,席玉佩
(湖北大学数学与统计学学院, 应用数学湖北省重点实验室, 湖北 武汉 430062)
0 引言及主要结果
F0⊃F1⊃…⊃Fn⊃Fn+1⊃…,
其中F0=[0,1]2, 且对任意n∈, 如果n∈Ej, 则对Fn中的每个方块以Fj方式生成Fn+1.令

设Q∈D, 用s(Q)、|Q|依次表示方块Q的边长、直径. 记
(1)
其中n(k)=Pj当且仅当k∈Ej,ε(k)=εj当且仅当k∈Ej.则Dn内包含Nn个边长为δn的内部两两不交的坐标方块. 记
(2)
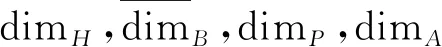
定理1设F=F({Fj},{Ej})为平面数字限制集, 则
记
其中对集合A,#A表示集合A的元素个数, 则
带入上述定理1及(2)式得下面推论.
推论1设F=F({Fj},{Ej})为平面数字限制集, 则
称度量空间X是s-齐性的, 如果存在常数C≥1, 使得对任意0 dimA(X)=inf{s≥0:X是s-齐性的}, 称之为X的Assouad维数[2]. 记 (3) 其中Nk,δk如(1)式定义. 本研究得到了平面数字限制集F=F({Fj},{Ej})的如下Assouad维数公式. 定理2设F=F({Fj},{Ej})为平面数字限制集, 则 dimA(F)=t*. 记 代入上述定理2及(3)式得下面推论. 推论2设F=F({Fj},{Ej})为平面数字限制集, 则 本节先回顾定理证明中用到的维数的记号及定义(参考文献[3,6]). 同时给出定理证明中用到的引理. 设集X⊂Rd,s>0.定义 dimH(X)=inf{s:Hs(X)<∞}=sup{s:Hs(X)>0} 为X的Hasudorff维数. 我们将用下面质量分布原理估计定理1中集合F的Hausdorff维数的下界(文献[3]). 引理1[3]设集X⊂Rd, μ是X上的质量分布,s>0, 若存在c>0,δ>0, 使得 μ(U)≤c|U|s 对所有满足|U|≤δ的集成立, 则dimH(X)≥s. 设δ>0, 记Nδ(X)表示直径不超过δ的覆盖X的集合的最少个数, 定义 为X的上盒维数. 定义 为X的s-维予填充测度, 其中称球族{Bi}={B(xi,ri)}为X的δ-填充(也可以用坐标方块族作填充), 如果i≥1,xi∈X,ri≤δ, 且Bi∩Bj=φ(i≠j).令 为X的予填充维数. 下面引理说明予填充维数恰是集合的上盒维数(文献[6]). 定义 为X的填充测度, 令 dimP(X)=inf{s:Ps(X)<∞}=sup{s:Ps(X)>0} 为X的填充维数. 下面引理说明集合的局部结构满足一定条件时, 其填充维数与上盒维数相同(文献[3]). 引理 3[3]设集X⊂Rd是紧集, 若对任意与X相交的开集V有 本节分三步证明定理1. 定理1的证明第一步, 证明dimH(F)=s*. 先证dimH(F)≤s*, 由(2)式, 对于任意t>s*, 存在{ni}, 使得 所以dimH(F)≤t.由t的任意性得dimH(F)≤s*. 再证dimH(F)≥s*, 由(2)式, 对于任意t (4) (5) 则U至多与9个k级方块相交. 从而由(4)式和(5)式得 其中c依赖于min{ε1,ε2,…,εm}.由引理1得dimH(F)≥t, 由t的任意性知, dimH(F)≥s*. 第三步, 证明dimP(F)=s*. (6) 定理2的证明先证dimA(F)≤t*.对任意s>t*, 由(6)式, 存在M(s), 使得当n>M(s)时, 有 进而任意n>M(s), 任意k≥1有 n(k+1)×…×n(k+n)≤(ε(k+1)×…×ε(k+n))s (7) 任给集U满足R:=|U|<δM(s), 存在k0≥M(s), 使得 (8) 任给r>0, 设A⊂U∩F为r-分离集, 对r, 存在k1≥k0+M(s), 使得 (9) 从而U至多与9个k0级构成方块相交, 进而至多与9n(k0+1)×n(k0+2)×…×n(k0+k1+1)个k0+k1+1级构成方块相交, 且每个k0+k1+1级构成方块内至多含有A中的一个点, 结合(1)、(7)~(9)式得 #A≤9n(k0+1)×n(k0+2)×…×n(k0+k1+1) ≤9N2(ε(k0+2)×…×ε(k0+k1))s 其中N=max{P1,P2,…,Pm}.所以dimA(F)≤s, 由s的任意性, dimA(F)≤t*. 再证 dimA(F)≥t*.对任意s n(kl+1)×…×n(kl+ml)≥(ε(kl+1)×…×ε(kl+ml))s (10) #A=n(kl+1)×n(kl+2)×…×n(kl+ml) ≥(ε(kl+1)×ε(kl+2)×…×ε(kl+ml))s1 预备知识及引理



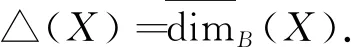
2 定理1的证明
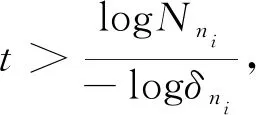



3 定理2的证明

