双局域共振Helmholtz声子晶体带隙研究

2019-02-19赵静波贺子厚

人工晶体学报 2019年1期

陈鑫，姚宏，赵静波，张帅，贺子厚

(空军工程大学基础部，西安 710051)

1 引言

自1992年声子晶体研究开始以来，已取得很大进展[1-2]。2000年，刘正猷首次提出局域共振型声子晶体[3]，由于其与Bragg型声子晶体相比，能够实现小尺寸控制大波长的特性，成为声子晶体发展的重点。近年来，为实现“低频，宽带，强衰减”的设计目标[4]，国内外学者对于声子晶体的材料参数和结构参数做了很多研究，并不断有新的原理引入声子晶体结构设计。其中，Helmholtz共振腔利用了空气自身的共振作用，因此可以选用轻质材料进行结构构建，对声子晶体的轻质化有天然的优势。2005年，Hu等[5]研究了一种典型了Helmholtz型声子晶体的带隙特征和隔声性能。包凯等[6]设计了一种嵌套型开缝圆管声子晶体结构，相对于开缝单管结构，打开了低频带隙，其第一带隙范围在290～460 Hz左右。Jiang等[7]采用多腔的方式构建出一种Helmholtz型声子晶体，将带隙降到了62.1～109.3 Hz的超低范围内。

但当前基于Helmholtz共鸣腔的声子晶体，由于带隙上下限往往均与腔体体积有关，造成带隙向低频方向移动的同时，其上限也在不断降低，形成了低频与宽带之间的矛盾。本文构建了一种新型的Helmholtz型声子晶体，通过将结构设计为内外腔的形式，摆脱了内腔体积对带隙上限的影响，使得带隙上限得以大大提高。运用理论等效模型和有限元计算两种方法对该结构的带隙机理、影响因素等进行了分析，得到了兼顾低频与宽带的结果。于此同时，将弹性杆-弹簧模型引入晶体设计中，使得简化模型理论计算精度得以提高。

2 结构带隙与隔声性能

该声子晶体晶格结构如图1所示，其晶格常数为a，由4个U字型结构嵌套组成，各边壁厚统一为b，各边之间留有宽度为s的空隙作为空气通道，为使四角构成边长l=s+b的正方形，控制最外层边长l1=a-2s-2b，中间边长l2=a-2s-2b，最内层边长l3可进行调节。在此结构中，形成了中间和四角两种大小的Helmholtz共鸣腔，由此形成一种腔体-细长管-腔体形式的Helmholtz局域共振型声子晶体。另外，由于一般固体，如钢、陶瓷等的声阻抗约为空气的105倍，可以认为其分界面为“硬声场边界”[8-9]，即将U字型结构视为刚体，忽略声波透过空气与其分界面而激起的振动。

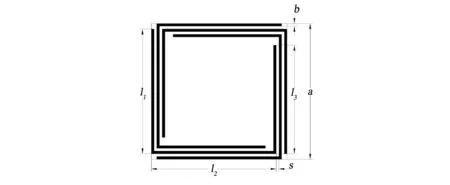
图1 结构横截面示意图 Fig.1 The schematic diagram of the structure cross section

将结构参数设置为a=100 mm，b=1 mm，s=1 mm，l3=90 mm，利用COSOL Multiphysics软件，运用有限元法对结构的特征频率进行求解，得出其能带结构如图2(a)所示。从图中可以看出，该结构在1400 Hz以下共出现了4条带隙，各带隙范围分别为86.9～445.9 Hz、464.07～902.52 Hz、905.71～905.73 Hz、916.9～1332.2 Hz，各带隙的起止点已在图中标出。

图2 (a)能带结构图；(b)隔声曲线 Fig.2 (a)Band diagram;(b) the transmission spectra

为研究该结构的隔声性能，将5个元胞沿纵向串联，并将横向定义为无限周期结构，结构的一端布置背景压力场，并设置完美匹配层(PML)，利用声压模式的隔声量计算公式针对0～1400 Hz范围内的声波进行隔声量计算：

(1)

其中，T代表隔声量，Pout代表出射声压，Pin代表入射声压，结果如图2(b)所示。从图中可以看出，隔声峰与带隙计算结果吻合良好，其中第三带隙由于过窄在隔声曲线中并没有体现。该结构隔声量在1140 Hz左右达到最大值178 dB，对于第一带隙范围内，在316 Hz左右达到最大值148 dB，而150 Hz左右的低频域也可达到102 dB。

3 带隙形成机理及其等效模型构建

对于声子晶体隔声材料，最关心的是其低频隔声性能，所以这里只就其第一带隙的振动模态进行讨论。

A、B两点的声压如图3所示，在A点，中间的腔体(内腔)声压最大，而四角的小腔体(外腔)声压基本为0，表明在此处由于声波的激励，细管中的空气与内腔中的空气产生了局域共振，声波被局域在内腔内，无法继续向前传播，由此对应于带隙的下限。

在B点处，内腔声压基本为0，而外腔中，声压基本相同但相位相反，表明在此处细管中空气与四角外腔内空气产生共振，与内腔无关。而随着频率的继续升高，声波开始向临近结构的内腔传播，由此对应于带隙的上限。对于局域共振型声子晶体，比较常用的等效模型为弹簧振子模型，下面，以此模型为基础，对其带隙形成机理进行分析。

图3 (a)模态A声压图；(b)模态B声压图 Fig.3 (a)Acoustic pressure distribution diagrams of point A;(b)Acoustic pressure distribution diagrams of point B

对于A模态，由于细管内空气体积相比内腔小得多，且细管宽度较小，假设细管内空气作同步运动且不计其受到的压缩，即可以视为振子；而内腔内空气忽略其振动造成的惯性力，即视为弹簧。与此同时，由于结构的严格对称性，可以只取结构的1/4进行计算，由此该模态振动可等效为图4(a)所示的弹簧-振子模型。

其等效质量和等效刚度的表达式分别为：

MA=sρ(l1+l3-b)h

(2)

(3)

其中ρ为空气密度，c为空气中声速，SA为内腔横截面积。

则其共振频率计算公式为：

(4)

对于B模态，细管内空气体积与外腔体积相差不大，再将其视为集中质量的振子会产生较大的误差。在此，将细管内空气视为一根做纵向振动的等截面杆，其一端为自由端，另一端连接着弹簧系统，并同样只取一个外腔及其连接的细管进行计算，其等效模型如图4(b)所示。

设杆上距自由端x处截面的纵向振幅为：

(5)

其中ω为角频率，A1及A2为待定系数，则其边界条件为[10]：

(6)

其中EB=c2ρ，为空气的体积模量，KB=ρc2s2/(s+b)2，为四角小腔体的等效刚度。将(5)式带入(6)式，经整理后可得：

(7)

这是一个超越方程，借助数值解法可以求出其第一阶固有频率，即为B模态的共振频率。

图4 (a)模态A等效模型；(b)模态B等效模型 Fig.4 (a)The equivalent model of point A;(b)the equivalent model of point B

4 带隙影响因素研究

为研究各结构参数对带隙的影响，运用有限元和等效模型理论计算两种方法分析计算了其第一带隙随参数改变的变化情况，得出的结果如图5所示。

图5(a)显示了第一带隙与晶格常数a的关系，计算中保持l3=10 mm。从图中可以看出，随着a的增大，带隙上限和下限均朝低频方向移动，同时带隙宽度有变窄的趋势。这是因为晶格常数增大会导致内腔体积变大，根据式(3)，其等效弹性模量相应减小，使得带隙下限向低频方向移动。与此同时，因为仅保持l3不变，但l1会随a增大而增大，由式(4)和式(7)，这会导致带隙上下限均向低频方向移动。另外，在a=0.02 m处，理论计算值发生了较大的偏差，这是因为此时内外腔体积与吸管内空气体积比值较小，已不能忽略腔内空气质量和细管内空气体积模量的影响。

图5(b)显示了第一带隙与管壁厚度b之间的关系，在此将晶格常数a固定为50 mm，随着管壁增厚，带隙上限下降，下限提高，带隙宽度变小。分析其原因，这是因为管壁的变厚会增大外腔体积而减小内腔体积，并分别使其等效弹性模量减小和增大。这说明对于该结构，在保证一定强度的基础上，使用轻薄的材质有利于获得更好的隔声效果，有利于隔声材料向“轻质”的方向发展。同时，经计算，带隙上限的理论计算误差稳定在3%左右，而带隙下限的误差从3%逐渐增加到7%左右，这是因为随着b的增加，内腔体积变小，要取得更为精确的带隙下限结果，也应采用弹性杆-弹簧模型。

如图5(c)所示，随着细管宽度s的增大，带隙上下限均向高频方向移动，但带隙上限的变化幅度低于带隙下限。这是由于在保持晶格常数不变的情况下，对于带隙下限，由式(4)可以看出，s的增大会直接导致共振频率的上升，且会使得内腔面积SA相应减小，进一步导致共振频率提高。而对于带隙上限，由于在式(7)中s的增大会导致方程等号左右两侧均减小，削弱了参数s的作用。另外，需要指出的是，随s增大理论计算误差也在增大，说明此时在进行定量计算时，同晶格常数a较小时的情况类似，需要综合考虑腔内空气质量和细管内空气体积模量。

图5(d)表征的是随l3增大带隙的变化情况，从图中可以看出，随l3增大，带隙上下限均向着低频方向移动，但带隙下限变化程度明显低于带隙上限的变化程度。这是因为由式(2)和式(3)可得，l3的增大会使等效振子质量增大，但与此同时，SA相应减小，从而导致等效弹簧模量增大，阻碍了带隙下限的进一步降低；而对于带隙上限，l3并不影响其等效弹簧模量。这说明对于该结构，在保证一定低频效果的同时，适当减小l3的长度，就可以出现较宽的带隙。

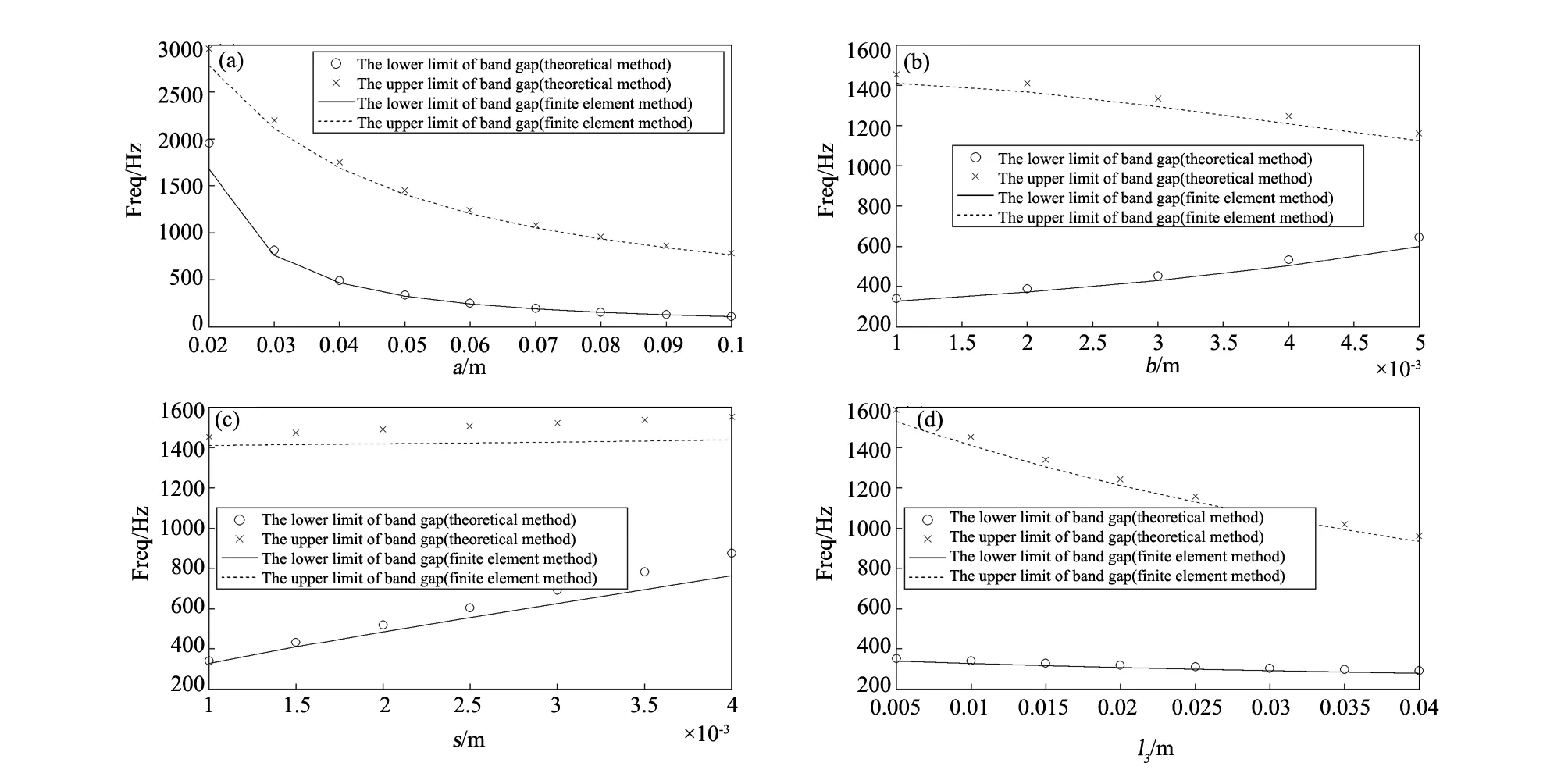
图5 (a)晶格常数a,(b)壁厚b,(c)细管宽度s,(d)边长l3对第一带隙的影响 Fig.5 The impact of (a)the parameter a;(b)the parameter b;(c)the parameter s;(d)the parameter l3 on first low frequency band-gap