函数值域的求法分类例析

2018-10-22山西省吕梁市贺昌中学高永亮

中学数学杂志 2018年19期

关键词：对应点值域定义域

☉山西省吕梁市贺昌中学高永亮

高中数学中，函数部分是重点也是难点，其中求函数的值域（求函数的最大、最小值）尤为重要.在这里笔者做了一个相对系统的整理，供广大高中数学教师与学生在学习过程中参考与使用.

一、直接法

例1求函数（fx）=的值域.

解析：由3x+1∈（1，+∞），得（fx）=故函数（fx）=的值域为（1，3）.

二、配方法

例2已知函数（fx）=x2-4x+1，x∈［-2，5］，求函数y=（fx）的值域.

解析：由（fx）=x2-4x+1=（x-2）2-3，

故当x=2时，ymin=-3；当x=-2时，ymax=13.

因此函数（fx）=x2-4x+1，x∈［-2，5］的值域为［-3，13］.

说明：在高中，二次函数y=ax2+bx+c（a≠0）在求其值域等其他问题时，一般采用配方将其化为形如再通过二次函数的性质，求其值域或解答相关问题.

三、判别式法

例3求函数的值域.

解析：由得函数的定义域为R，原式可化为：（y-1）x2+（1-y）x+y=0，当y=1时，x∈∅.

当y≠1时，又x∈R，我们把上式看成关于x的一元二次方程，得Δ=（1-y）2-4y（y-1）≥0，解得

说明：此类型的分式函数，特别是定义域为R的分式函数，通常将其变形得到形如关于x的二次函数，再采用判别式大于等于零求函数的值域是一种很好的方法.

四、分离常数法

因此原函数的值域为{y|y≠1}.

说明：此类型的函数，分子、分母都含有自变量，而通过分离常数法，可以将此类函数的变量只含到分母上，分子化为常数，使函数值y的范围变化容易确定，从而较为简单地求出函数的值域.

五、换元法

例5求函数的值域.

解析：设从而得（fx）=g显然函数g（t）在［0，+∞）上为单调递减函数，所以g（t）≤g（0），因此原函数的值域为

说明：若所求函数是含有根式结构的函数，通常采用换元法，通过变形将无理式化为我们熟悉的有理式，再进一步求出函数的值域（.事实上，从本质而言，这类函数就是二次函数）

六、利用函数的单调性

例6求函数的值域.

解析：易得函数的定义域为

说明：通过判定函数的单调性，再求函数的值域，能做到事半功倍.利用函数的单调性，求函数的值域是一种重要方法.对于本类题型，也可使用题型5的解法.

七、图像法

例7 求函数y=|x-1|+|x+3|的值域.

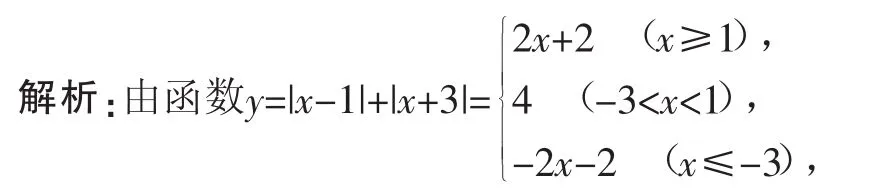
作出其简图（图略），通过图形易得函数y=|x-1|+|x+3|的值域为［4，+∞）.

八、利用几何意义法

例8求函数y=|x-1|+|x+5|的值域.

解析：由绝对值的几何意义，式子|x-1|+|x+5|表示数轴上任一数x对应点P到数1与数-5对应两点A、B的距离之和，在数轴上容易得到线段AB上的点到此二点距离之和最小为6，其他点到此二点距离之和恒大于6，因此函数y=|x-1|+|x+5|的值域为［6，+∞）.

说明：在数轴上|x|的几何意义是：数轴上任一数x对应点P到原点的距离；在数轴上|x-a|的几何意义是，数轴上任一数x对应点P到数a对应点A的距离，即|PA|之长.

九、利用公式|a|-|b|≤|a±b|≤|a|+|b|

例9求函数y=|x-1|+|x+5|的值域.

解析：由公式得y=|x-1|+|x+5|≥|（x-1）-（x+5）|=6.

因此函数y=|x-1|+|x+5|的值域为［6，+∞）.

说明：不等式|a|-|b|≤|a±b|≤|a|+|b|，是求最大、最小值与证明不等式的常用公式之一，如果能灵活应用，问题的解答就特别简单了.

十、利用基本不等式

基本不等式是高中数学中求最大与最小值（求值域）常用的一种基本方法之一，在使用中要求关系式满足：一正、二定、三相等的条件.

十一、三角换元法

基本不等式、三角函数、二次函数、求导是高中数学中求最大与最小值（求值域）最常用的四种方法.三角函数是通过利用正弦函数与余弦函数的有界性，即|sinx|≤1，|cosx|≤1，从而解答有关三角函数问题的最大与最小问题，本类问题的关键是通过合理的三角换元把函数最值问题转化为三角函数问题，进一步求出所求函数的值域.

十二、利用定义域求值域

例10求函数的值域.

解析：由函数得ex-e-x≠0，易得函数的定义域为{x|x≠0}.

说明：先求出函数的定义域，再通过变形把含自变量x的式子移到一边，把含y的式子移到一边，再通过函数的定义域直接转化为关于y的式子的范围，进一步求出y的取值范围，即求出函数的值域.这种方法，理论上是总成立的，它采用数学中的转化思想，把函数的定义域转化到函数的值域.只不过有的时候这种转化甚为麻烦，我们根据实际情况，合理使用，不要过于死板.