教之道在于悟——从问题思考解题教学

☉江苏省张家港市暨阳高级中学 周晓宇

解题教学最终的目的是会运用数学知识解决数学问题，尤其是对高考数学真题的求解.但每每总有很多学生感觉真题难、无从入手.笔者以为，这样的现象若是普遍存在于教学过程之中，可以说明教师对于解题教学的研究不足，导致学生对于解题的掌握不够，以及数学素养和能力的缺失.

当下中学数学教师对于真题和教材的联系是比较缺乏思考的，可能是难以发现这种思考，也可能是忙于各种事物而缺乏思考的时间，总之复习教学效率低下是共识.笔者想借助几道高考真题结合教材的知识、性质和原题，来谈一谈教之道如何悟.

一、数学概念的悟

数学概念是高考必定考查的重要方向，但是如何考查却是各有神通，一般来说概念的考查以简单运用为主，这可以考查大部分学生对于数学概念的掌握程度，偶有概念的考查以能力立意为上.因此感悟教材中的概念从而解决高考真题的教学成为复习教学特别需要关注的点.

例1（2015年浙江卷改编）存在对应关系f，对任意x∈R，下列对应关系不是函数法则的是_____.

（1）f（x2+4x）=|x+2|；

（2）f（x2-1）=|x+1|；

（3）f（x2-4x）=|x+2|；

（4）f（x2+1）=|x-1|.

分析：笔者将原题稍加改编，本质未做改变.对于学生而言，初识本题，似乎并无头绪.静下心来思考，本题到底考查什么？题意中说对应关系和对应法则，应该不难想到这是一道与函数概念相关的问题.比较简单的函数概念判别试题，往往是对函数概念进行简单的一对一、多对一的思考辨别，而本题显然不属于简单问题.我们知道，函数关系是一种特殊的映射关系，而映射关系又是特殊的一种对应关系，因此找准非空数集和函数概念就可以解决问题.比如，对于（2），不妨取x=±1，则x2-1=0，也就是说f（0）=2或f（0）=0，从函数关系的角度来说，同一个自变量对应不唯一的y值，从而并非是函数关系，而是一种一般的对应关系.其余选项可同样排除，所以答案是（2）（3）（4）.

说明：数学概念的深刻“悟”是困难的，因为这势必需要对概念的方方面面有全面的理解.以函数概念为例，教会学生要从概念最本质的特征入手思考——“一对一”“多对一”是函数对应关系，“一对多”一定不是函数关系.

二、数学性质的悟

数学性质是教学中教师最为关注的.但是随着大量模拟试题的训练，师生往往都忽视了这些教材基本性质，还一味地埋头寻找技巧和技能，这种教学是得不偿失的.教材中的数学性质有哪些？比如等差数列所拥有的函数本质，通项是一次函数的本质，求和公式是二次函数的本质；椭圆、双曲线拥有的基本性质，如对称性、离心率、渐近线等，围绕这些基本性质结合试题的思考是解题教学的重要感悟.

例2等差数列{an}的前n项和为Sn，满足S30=S60，则下列结论中正确的是______.

（1）S45是Sn中的最大值；

（2）S45是Sn中的最小值；

（3）S45=0； （4）S90=0.

分析：本题是高三一次联考中的数列问题，笔者以为本题的命制是比较凸显了回归教材的基本理念.学生的思维总是显得那么直白——利用首项和公差去计算两者之间的关系，进而逐一验证每一项的正确性，这种解决方式我们称之为基本量解决方式，好处是思维极为简单，但是运算量较为复杂，显然这样的解答不是命题者的本意.从数学本质来说，等差数列的本质如下表所示：

通项公式 函数本质 求和公式 函数本质等差数列 an=dn+a1-d 一次函数Sn=d（ ）n 2n2+a1-d2形如Sn=An2+Bn过原点的二次函数

因此，我们可以从函数本质的角度来思考数列，使用数列的函数特性进行研究.等差数列求和公式的函数本质是形如Sn=An2+Bn的二次函数，且该二次函数必过原点，因此根据S30=S60可以推出其对称轴为n=45，所以S45可能为最大值，也可能为最小值，显然（1）和（2）的说法都是片面的，而S90=0则是显而易见的，正确结论只有（4）.笔者以为利用正确的数学性质去感悟数学问题，大大增强了学生对数学知识的理解和运用，这才是教之道在于悟的更高境界.比如在教材习题中还有这样的问题，值得教师去挖掘和深思：

教材习题：等差数列{an}的前n项和Sn=m，前m项和Sm=n（m≠n），求前m+n项的和Sm+n.

两位对教材性质理解不同的学生，其解答我们来看一看：

生1：设{an}的公差为d，则由Sn=m，Sm=n（m≠n），得

辨 析：生1利用基本量运算，Sm+n=a1（m+n）+，只需求出即可，由Sn，Sm可以构造出并求出；生2利用数学性质——函数思想，理解等差数列前n项和Sn满足的关系从函数的角度而言，是必过（0，0）点的二次函数，借此突破，高效省事.两种方式孰优孰劣，一眼便知.因此可以说，数学性质的悟恰是数学教学更高的境界，是提升学生数学素养的必经之路.

三、数学思想的悟

教之道在于悟，要从更高的境界去悟.笔者以为这种高境界需要从思想层面去认识、去感悟.可以这么说，数学思想是教学的更高境界.数学思想蕴藏在何处？蕴藏在教材之中，这种挖掘是需要时间积累、慢慢体会的，以向量为例，为什么这多学生对于向量的学习始终停留在学习的表面？这个原因笔者可以这样认为：第一，向量是不同于数量范畴的学习，很多学生依然停留在数量范畴思考.第二，平面几何知识的薄弱，向量的另一特性是其方向性，即几何特征，中学数学向量仅仅涉及平面向量和空间向量，几何特征往往比代数特征来得更为有效，因此不会运用几何特征解决问题势必没有感受到向量的图形思想.

说到底，向量学习主要是数形结合思想的贯穿——即以数解形的运用和以形辅数的魅力！我们来体会下述问题.

例3 （2011年全国卷理12）设向量a，b，c满足|a|=|b|=1，a·b=则|c|的最

大值等于______.

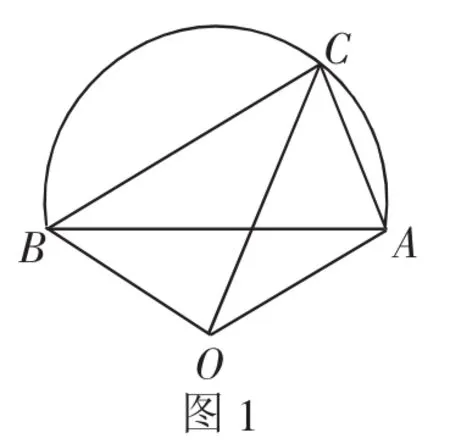
分析1：考虑到本题的结构，可以从数形结合思想的角度入手，显然向量a，b满足夹角120°，且a-c与b-c夹角是60°，思考此处的平面几何性质——对角互补的四边形必定四点共圆.因此，以四点共圆来建构图形.如图1，设可知点C的轨迹是优弧（，显然当点C为优弧的中点时取到最大值，即为O，A，B，C四点所在圆的直径，得在△ABC中，由正弦定理

分析2：本题也可以从数量积出发，利用代数运算，结合不等式的视角进行.

说明：显而易见，本题一般都不会从代数方式入手，几何特征的图形化思想，即数形结合思想是问题解决的主要方式.中学数学属于初等数学，因此在二维数量关系和三维数量关系中，几何特征往往是解决中学数学问题的首先方式，这一点在高考真题中已经频频出现，成为一种共识.

总之，解题教学不能完全依赖题海战术，这种落后的方式已经不受新课程改革的青睐，效率已经极为低下了.从教材中去悟概念、悟性质、悟思想，让教学围绕这一层次逐步深入，才是当下解题教学的关键.