动静变换法在数学解题中的应用

☉江苏省南京市秦淮中学 朱 佳

动与静是对事物状态的一种定性描述，从哲学角度来看，动与静是一个统一体，可以相互转化.因此数学上的问题条件也可以进行动静划分，基于动静原则进行变换.对于一些复杂问题，合理采用动静变换策略可以有效破除思维屏障，获得解题的思路，下面将具体阐释动静变换策略在解题中的应用.

一、以动求静，化不等式

物体的静止是相对的，同样地，在数学中静态下的问题也是相对存在的，如代数等式、不等式、分子式等，有时从静态的角度对其直接变形求解较为繁杂，难以获得较好的解题效果，此时可以尝试考虑运用一定的策略将其转化为动态问题，可能会收到意想不到的结果.一般对于代数问题可以将其等效转化为几何上的距离问题，通过距离的取值来构建代数关系.

例1已知不等式试求不等式的解.

分析：上述不等式由于具有根号，直接求解相对较为复杂，可以采用以动求静的解题策略，将静态的不等式化为动态的平面几何区域问题，通过求区域的取值范围来解不等式.

解：对原不等式进行变形，得6，对应的可以构建一个平面区域：6，表示a=3，c=2的椭圆及其内部的区域，即如图1所示，令y=2，解得即不等式的解就为

在对直角坐标中的区域划分、求解析几何中的曲线运动轨迹时可以引入不等式，这就为代数不等式的求解提供了一个思路，即通过对不等式变形，将其等效为一个动态变化的几何区域，通过对几何区域的取值来完成求解，这样的方式省去了代数移项、合并、变形的过程，使求解过程更为直观，是对以动求静优势的充分体现.

二、以静制动，解析轨迹

数学上存在众多的动点问题，往往由于点的动态轨迹难以捕捉而造成求解的困难，此时可以考虑对条件进行设定，使动态问题转化为相对静止的状态来研究，如解析几何中的动点问题可以考虑研究某特殊点的位置，或直接建立动点与静态条件之间的关系，也可以设定某一运动参数，使其转化为相对意义上的静态问题.

例2已知双曲线过定点A（2，1）的直线l与双曲线C的图像相交于点P1，P2，设线段P1P2的中点为点P，试求点P的运动轨迹方程.

分析：由于直线l的斜率不确定，则直线与双曲线图像的交点也不确定，因此随着直线l的斜率变化，中点P也会变化，因此，从严格意义上来说，求轨迹方程是动态问题.由于其轨迹较为抽象，可以采用以静制动的方式.

设P（x0，y0）是一个相对静止的点，可构建一条确定的直线l的参数方程，然后利用参数的几何意义，建立关于x0，y0的函数关系，进而研究中点P的轨迹.

解：设点P的坐标为（x0，y0），可得直线l的参数方程（t为参数），联立直线方程和双曲线解析式，可得（2cos2θ-sin2θ）t2+2（2x0cosθ-y0sinθ）t+2x02-y02-2=0.由于点P为直线与双曲线相交弦P1P2的中点，则有t1+t2=0，即2x0cosθ-y0sinθ=0，联立直线的参数方程，结合定点A的坐标，消去未知角θ，可得2x02-y02-4x0+y0=0，用x，y代换其中的x0和y0，可得中点P的轨迹方程为2x2-y2-4x+y=0.

以静制动在数学解题中有两种应用方式，一是研究动态问题的特殊状态，然后推演整个问题，如特值法；二是将动态问题转化为相对意义上的静态问题，如参数法.本题目中采用的就是解析几何上常用的参数法，用自变量参数来静态描述点的运动轨迹，从而实现问题的求解，其解题策略具有一定的推广价值.

三、动静互换，简求最值

物体的运动和静止是相对的，因此可以互换，同样地，数学的研究对象也可以进行互换，即在某些问题中对条件进行设定，使动态条件和静态条件进行互换，然后通过研究新的问题条件来求解.由于这种互换是一种整体互换，因此在特定情形下的求解是合理的，最为常见的是动点到定直线或动点到定点的距离问题，条件互换后的距离依然不变.

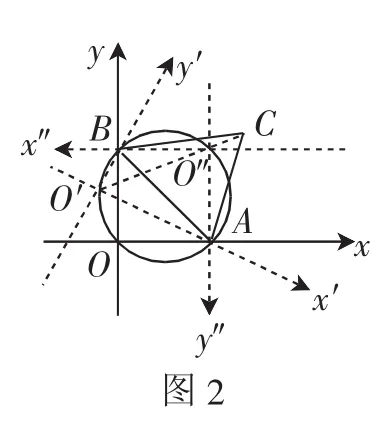
例3如图2所示，△ABC为等边三角形，且三角形的边长为2，其顶点A在坐标的x轴上运动，顶点B在y轴上运动，设点C到坐标原点O的距离为d，试求距离d的最值.

分析：因为点A和B分别为x轴和y轴上的动点，则导致三角形的另一顶点C也必然会相应的运动，距离d的取值会随之变化.原始坐标轴静止，几何三角运动，直接求解的方式难以获得距离d的最值，可以采用动静互换的策略，假设△ABC为静止不动，则根据运动的相对性，可视坐标轴运动，原点O的运动轨迹规则可循，可对其进行几何等效，通过分析几何距离求解.

解：假设△ABC为静止，坐标轴运动，已知∠AOB=90°，则点O可以视为是在以AB为直径的圆上运动，问题就可以转化为求点C到以AB为直径的圆上点的距离最值，因此当直线CO经过AB的中点时可以分别取得最大和最小值.分析可知只有当△AOB是以AB为斜边的等腰直角三角形时d可以取得最值.当O运动到AB的左下侧位于点O的最远端，此时d取得最大值；运动到AB的右上侧位于点O的近端，此时d取得最小值

数学上的条件动静互换是相对意义上的互换，用以研究问题的核心要素，而忽略了某些细枝末节问题，因此在互换时需对其进行评估，确保条件互换不会对问题本质造成影响.另外这种互换是一种整体互换，因此解题时需要对问题中的条件进行动静归类，然后进行全盘互换，确保求解准确.

四、动静结合，释解几何

物体的动与静之间存在着相互制约的关系，这种关系可以合理用于数学解题，利用动静条件之间的互为补充、相互完善的特性来全方位的研究问题对象.在解题时要灵活处理条件“动”与“静”的关系，充分降低问题的思维难度，高效解题.

例4图3所示的为一棱长等于2的正方体ABCD-A1B1C1D1，已知E为棱长BC的中点，点P在线段D1E之上，设点P到棱CC1的距离为d，试求d的最小值及此时点P的坐标.

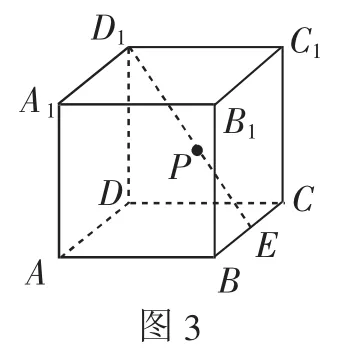
分析：求解立体几何的最值问题，可以采用动静结合的方法，即首先需要建立空间坐标，确定相关点和向量的坐标值，实现条件的静态化.求距离d的最值，可以先将点P看成定点，然后在棱长CC1上取一动点Q，从而建立线段|PQ|的参数方程，求出其最小值的函数，然后将点P看作是动点，进一步研究函数的最值，最终确定|PQ|的最小值.

解：以点D为坐标原点建立空间坐标系，如图4所示，因为点P在线段D1E之上，则一定存在λ（λ∈［0，1］），使得向量=λ（1，2，-2），进而可得点P的空间坐标为（1-λ，2-2λ，2λ）.在棱CC1上取一点Q，设其坐标为（0，2，z），则d的最小值就为点P和Q之间距离的最小值，将λ视为常数，则点P为定点，而Q为动点，P和Q之间距离的平方|PQ|2=（1-λ）2+4λ2+（2λ-z）2，z∈R，当z=2λ时，|PQ|2取得最小值，则然后使点P运动，即λ变化，设可知当时，y取得最小值，将λ代入点P和Q的坐标，得因此距离d的最小值为此时点P的坐标为

动静结合是数学解题较为常用的方式，可以利用条件的互补性来分析问题，立体几何上的动静结合则可以将动态的问题局部静态化，通过逐步分析来求解，是降低思维难度的有效方式.需要注意的是在进行局部静态化时要设定静态参数，但后续还需要对静态参数进行动态研究，确保结果的全面性和准确性.

从严格意义上说，动静变换策略是解题的一种思想方法，是思维层面的解题思想，可以降低思维的难度，指导问题的分析过程，是解题的辅助方法，因此在实际解题中要结合基础方法综合使用.另外在使用动静变换法时要掌握一定的策略，首先对问题进行动静分析、评估，然后基于动静原则对条件进行变换，完成求解.