凸四边形的若干翻折问题

赖 霖 徐新植 黄悦军

(广东省深圳市龙岗区坪地中学2019级7班 518117)

将一个凸四边形进行翻折，翻折前后四边形边长形成的夹角与所翻折的内角之间有何关系，笔者在老师的指导下进行了有关研究，并得到如下结论.

结论1 如图1所示，将四边形ABCD沿着直线EF翻折，点A的对应点为A′，且点A′在∠A的内部，那么有2∠A=∠DEA′+∠BFA′.

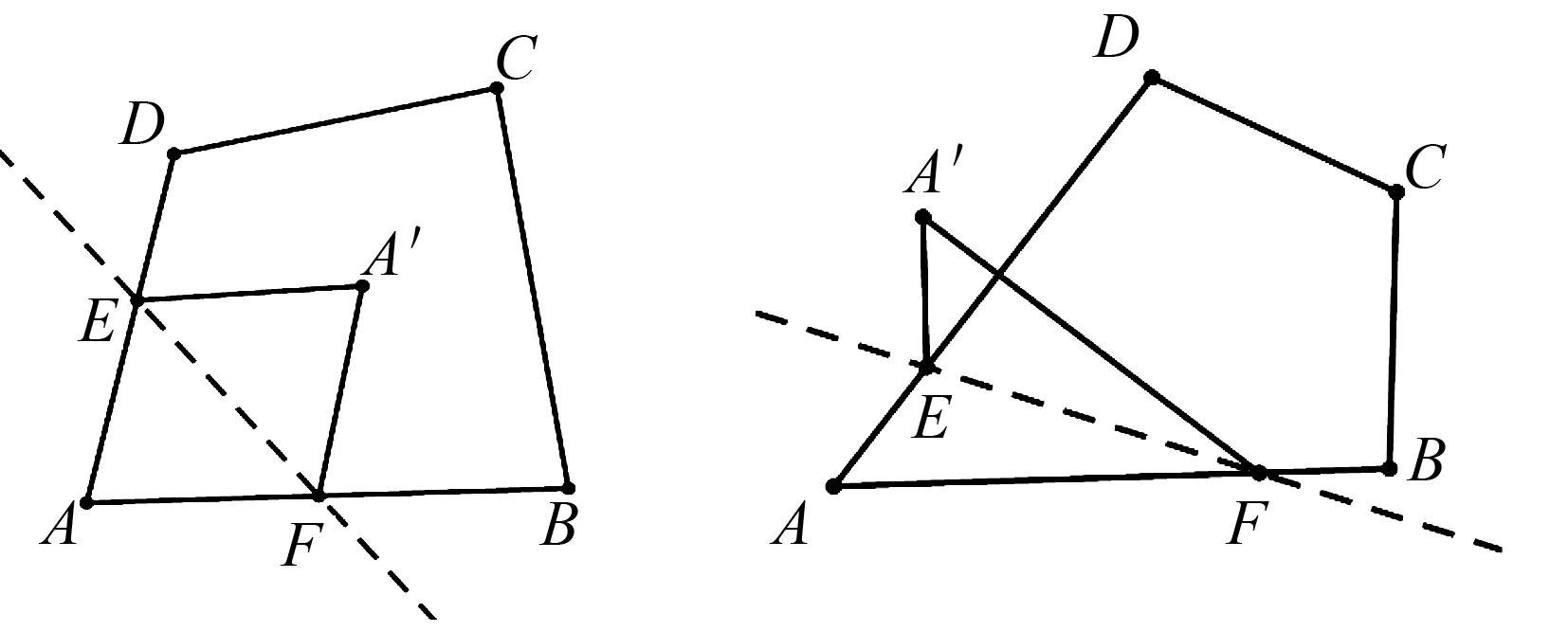
图1 图2

结论2 若将四边形ABCD沿着直线EF翻折，点A的对应点为A′，且点A′落在∠A的外部，那么有2A=|BFA′-DEA′|.

②点A′落在∠A的外部且如图3所示，由图2情况，同理可得2∠A=∠BFA′-∠DEA.从而有2A=|BFA′-DEA′|.

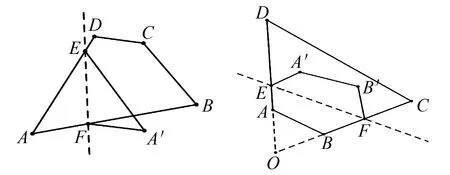
图3 图4

若翻折凸四边形的两个角，我们有以下结论.

结论3 如图4，若将四边形ABCD沿着直线EF翻折，点A的对应点为A′，点B的对应点为B′，DA与CB的延长线相交与点O,且点A′和点B′均落在∠O的内部，那么2(∠A+∠B)-(∠A′ED+∠B′FC)=360°.

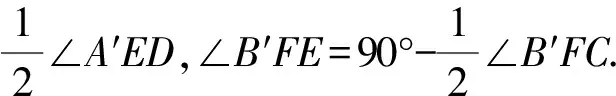
结论4 如图5，若将四边形ABCD沿着直线EF翻折，点A的对应点为A′，点B的对应点为B′，DA与CB的延长线相交与点O，点A′落在∠O的外部，点B′落在∠O的内部，那么2(∠A+∠B)+(∠A′ED-∠B′FC)=360°.

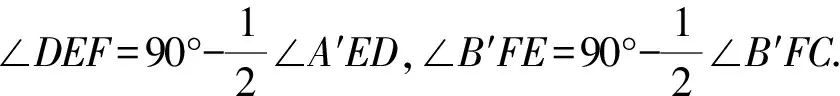
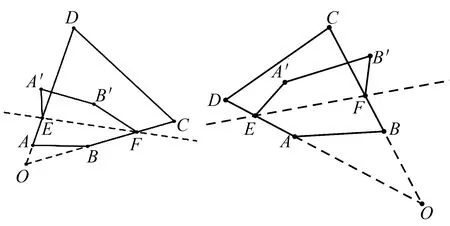
图5 图6

类似结论4的证明，我们可得结论5.

结论5如图6，若将四边形ABCD沿着直线EF翻折，点A的对应点为A′，点B的对应点为B′，DA与CB的延长线相交与点O，点A′落在∠O的内部，点B′落在∠O的外部，那么2(∠A+∠B)+(∠B′FC-∠A′ED)=360°.

结论6 如图7，若将四边形ABCD沿着直线EF翻折，点A的对应点为A′，点B的对应点为B′，AD与BC的延长线相交与点O，点A′和点B′均落在∠O的外部，那么2(∠A+∠B)+(∠A′ED+∠B′FC)=360°.

图7

关于其他多边形有关翻折问题，留给感兴趣的读者进行研究.