高中数学教学体系中的方程思想
2018-10-22江苏省海门中学
☉江苏省海门中学 张 婕
在高中数学学习的过程中,学生学习的目的并不仅仅只是要掌握知识,更要学会使用知识.在数学学习过程中,我们要让学生逐步体会隐含在知识背后的数学方法和思想,这些内容是数学课堂的精髓与核心,是学生进行学习和研究的关键所在.而在众多数学思想中,方程思想对学生理解数学知识、发展数学思维有着非常重要的作用.
一、高中数学教学中方程思想的作用
所谓“方程思想”,就是将方程作为刻画世界的一种有效模型,即从相关量的数量关系着手,用等式将有关内容衔接起来,最终在方程研究中完成对问题的分析和解决.在高中数学学习的一系列活动中,方程思想有以下几个方面的作用.
1.形成解题思路,促成问题的解决
方程思想在高中数学的习题处理过程中有着非常广泛的应用,一些问题本身就是围绕方程展开,或是讨论方程实数根的存在情形,或是讨论方程参数的取值特点,或是直接对方程进行求解.除此之外,方程也是学生分析问题的主要途径,很多问题只有写出对应的方程,我们才能实现求解,有些问题也存在其他的处理方法或思路,但是方程的应用可以简化处理的过程,或是让整个解决过程更显灵活.
2.发展学生思维,提升逻辑推理能力
面对很多以生活中的真实场景为素材来设计的问题,学生在处理时往往对相关素材进行分析,从中发现并提炼出有关的数量关系,然后由此来建立数学模型,并以方程的形式展示出来,这样的处理很难发展学生的思维.面对错综复杂的情境,学生首先要对其中的诸多隐含条件进行分析,对很多原生态的问题要进行数学化的分析和处理,这是建立模型和方程最为基础的要求,同时这也是方程思想的核心,这一过程对学生思维的发展以及逻辑推理能力的提升大有帮助.
3.串联知识体系,完善学生的认知结构
高中数学的教学是非常松散的,因此在数学教学的过程中,我们要注意引导学生对数学知识进行系统化建构.当我们要对知识体系进行建构时,我们要明白:黏合这些知识的是数学方法和有关思想,方程思想在其中就占据着非常重要的地位,无论是最开始集合概念的学习,还是不等式的研究,抑或解析几何问题的处理,每一块内容都隐含着方程的身影,因此我们结合方程来指导学生知识体系的建构,并且能够促进学生认识的系统化.
4.激活学生兴趣,充实他们的解题方法
在解题过程中,我们通过方程来指导学生进行处理,可以让问题的表征和分析更加简洁,学生也将从中感受到数学研究的奇妙所在,这也将让学生感受到数学学习别样的乐趣.因此将方程思想引入数学教学也是学生兴趣激发的需要,学生当然也会由此而充实他们的解题方法,这样的教学显然有助于学生思路的拓展,有助于他们综合素质的提升.
二、高中数学教学中方程思想的优势体现
在高中数学问题的研究中,方程思想在以下两个方面有着非常显著的体现.
其一,在某些等量关系复杂的问题中,往往涉及很多的量.在这种情形下,我们要引导学生去把握相等关系,并结合问题的需要来设计相应的未知数,最终围绕着未知量和已知量来建构方程,或者是方程组,并且在方程或方程组的分析过程中形成认识,这样的处理比一般化的数学方法要好上很多.
其二,在一些代数、几何综合性的问题中,方程思想也有着其独特的优越性.我们以方程为桥梁,可以让学生能够更快地明晰解题思路,并最终完成问题的解决.
三、方程思想在数学学习中的应用实践
在高中阶段的数学学习过程中,方程思想有着非常广泛的应用,下面我们就从一些具体的实例着手,在应用中进一步对相关思想和方法进行感悟和体会.
1.函数问题处理过程中的方程思想
函数历来与方程有着非常紧密的关联性,有方程的求解、根的存在情形、参数的取值范围等,这些都可以采用函数的方法来处理,甚至有时还要画出图像,如此即可让问题的处理更加快捷而高效.反之,有的时候函数问题也需要用到方程,方程思想的引入拓展了问题分析和解决的思路,可以让学生破解困局,得到新的问题解决灵感.
例1已知R并且x3+sinx-2a=0,4y3+sinycosy+a=0,求cos(x+2y)的值.
思路分析:如果按照一般化的思路,本题可以从三角函数求值的角度着手分析,即“角的拼凑”或是对两角和余弦公式进行变形处理,但是这样的分析过程将遇到相当大的困难,为此我们转换思路,以方程思想进行尝试与探索.
解析:由已知条件可得x与-2y是关于m的方程m3+sinm-2a=0的实数解.设(fm)=m3+sinm-2a,使用导数的有关理论可得该函数在上是单调递增的函数,因此当方程(fm)=0在上至多存在单一的实数解,因此可以知道x,-2y∈所以只能是x=-2y,于是有co(sx+2y)=1.
反思:本题对条件进行了抽象处理,得出了同一个方程的两个根,并结合函数的单调性可以推导出两个根相等,且整体上可以得到x+2y=0,进而顺利完成问题求解.这样的处理巧妙避开三角函数烦琐的变形,是方程思想提升问题解决效率的一个典型案例.
2.三角函数问题处理中的方程思想
提及三角函数,很多高中生都大皱眉头,原因无他,公式太过烦琐多变,而且很多公式大同小异,以致于学生很容易发生混淆.因此,在处理三角函数问题时,我们不能让学生将思维定格在公式应用上,我们应该鼓励学生将方程思想运用于其中,指导学生灵活运用相关的思想和方法来完成问题的分析和处理.
例2求sin18°的值.
解析:设18°=α,则2α=90°-3α,所以sin2α=cos3α,因此有2sinαcosα=cos(2α+α)=4cos3α-3cosα.因为cosα≠0,所以2sinα=4cos2α-3,即4sin2α+2sinα-1=0.解之可得sinα=结合上述范围最后可得到
反思:本题所涉及的角度并不是一个特殊角,所以如果希望通过两角和与两角差的公式进行求解,这是很难得到最后结果的.但是我们如果利用这个角度与90°之间的数量关系,并且构造出有关18°正弦值的一元二次方程,这样既可让学生在方程求解的过程中获得最后的结论,也可以收获化难为易的学习效果.
3.立体几何问题处理中的方程思想
方程是一种重要的数学工具,在很多问题处理过程中,我们通过方程可以沟通已知量与未知量之间的关系.这一点在立体几何的问题处理过程中也多有体现,但是有很多学生却出现着这样一些理解层面的偏差,他们认为,方程是代数,立体几何属于几何,这是两个泾渭分明的范畴,不能混为一谈,这种想法是片面而肤浅的,举例说明如下.
例3如图1所示的三棱锥P-ABC中,AB=1,AC=2,角平分线AD=1,各侧面积与底面所构成的二面角都等于60°,求解这个三棱锥的侧面积.
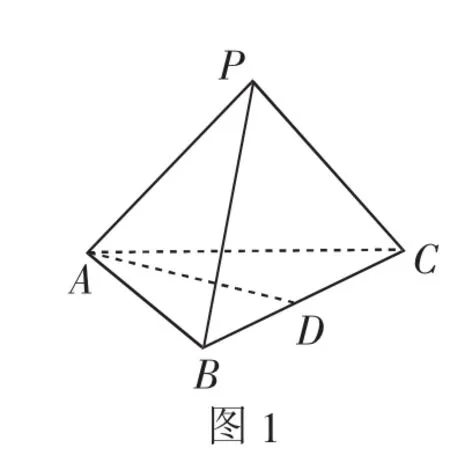
解析:假如BD=x,由内角平分线定理可得得CD=2x.因为∠BDA+∠CDA=180°,所以cos∠BDA+cos∠CDA=0.由余弦定理得,解出可得因此可以得到从而使得可得结论S=侧
反思:本题立足于角平分线这个条件,将变量BD引入问题分析,并两次使用余弦定理建立关于BD的方程,由此将立体几何的问题转变为平面几何的问题,这样的处理有助于学生避免烦琐的符号表示以及一系列的推理.
综上所述,在高中数学的教学过程中,教师要关注问题的分析和思考,要让每一个学生都能在学习过程中有所收获,这样的教学有助于学生更加全面地发现并认识问题,同时也有助于他们领会数学知识的真谛.
