一种指数渐消记忆加权滤波的内交点定位算法

高端阳，李 安，傅 军

（1. 海军工程大学 导航工程系，武汉 430033；2. 海军工程大学，武汉 430033）

2017年11月5日，我国成功发射两颗北斗三号全球组网卫星，开启了北斗卫星导航系统全球导航的新时代。随着卫星导航技术的发展和成熟，室外环境下的导航定位基本得到解决。但由于室内环境相对比较复杂，无线信号遮挡较为严重，多路径效应更为明显，GNSS系统在室内无法得到有效应用。因此，近年来室内定位逐渐成为了广大学者的研究热点和难点。目前，室内定位技术手段主要有无线定位方案、基于MIMU的行人推算方案、基于视觉技术的定位方案等，各种室内定位技术相映生辉，但依然没有一种普适的方案。

定位方法中可分为基于测距的定位算法和非测距的定位算法。基于测距的定位算法简单，计算量小，实时性好且容易实现。基于测距的定位算法又分为到达角定位[1](Angle of arrival, AOA)、到达时间定位[2-4](Arrival of time, TOA)、到达时间差定位[4-5](Time difference of arrival, TDOA)和基于接收信号强度[6](Received signal strength indication, RSSI)定位等，其中TOA定位算法为常用的一种解算方法，TOA误差主要受传播效应、时钟漂移和干扰影响[7-11]。文献[9]针对基于精确达到时间测量的定位系统，通过建立相关的测量误差模型可以实现较好的距离估计。文献[10]利用多路径散射模型分析非视距（Non Line of sight, NLOS）传播的影响，然后采用最大似然估计和贝叶斯估计目标与基站（Base station, BS）之间的距离。文献[11]提出了一种新的基于几何优化的位置估计方法，减轻多径衰落、非视距传播和多用户干扰等误差源的影响。

传统的迭代加权最小二乘定位算法已无法适应复杂的室内环境。针对室内无线定位系统中存在的非视距传播的问题，本文提出了一种内交点室内定位算法，该方法无需对视距环境还是非视距环境进行识别，也无需利用任何的先验信息，通过计算多个圆位置线之间的交点，然后建立几何约束模型，实现对目标位置的有效估计。同时在对实测数据分析的过程中，发现无线定位系统存在信号易跳变的问题，又提出了基于指数渐消记忆加权的测距滤波算法对各个基站测距值进行滤波，然后利用滤波后的数据进行目标位置估计，有效地削弱了信号的跳变。

1 迭代加权最小二乘定位算法

级迭代加权最小二乘法（Iterative weighted least squares, IWLS）是常用的一种测距定位算法，通过加权的方式可以有效地减小误差的影响，提高定位解算精度。以平面定位为例，假设目标到各个基站的测距分别为为目标与各个基站有效测距的总个数），在不存在测距误差的情况下，满足以下方程：

式(1)为非线性方程组，且通常为超定方程组，为求解该方程组，采用迭代最小二乘算法。首先预测目标初值为然后利用预测的目标位置计算预测距离可得以下方程组：

目标预测位置初值通常采用前一时刻的位置解。将测量距离和预测距离相减，并在预测位置处使用一阶泰勒级数展开，整理方程可得目标位置估计值如下：

式中测量矩阵H为：

在解算的过程中，由于存在线性化过程，单次解算误差较大。为了获得更高精度的定位解，将估计值作为下一次的预测值，通过多次迭代算法，若前后两次估计的位置解之差满足精度要求，则停止迭代，输出目标位置。

由于各个基站测距误差的存在，且各个基站测距误差特性不一致，通过加权最小二乘可提高目标位置解算精度。加权最小二乘目标位置估计可由下式表示：

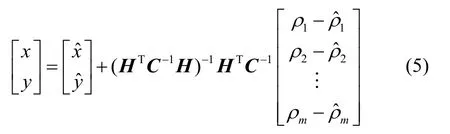
2 一种内交点室内定位算法

非视距传播是影响室内无线定位精度的关键因素之一。当某一基站与目标之间处于NLOS状态时，该基站的测距误差就会远远大于其他处于视距（Line of sight，LOS）环境下基站的测距误差，即出现图1所示的测距现象。

图1 NLOS环境下的基站圆位置线Fig.1 Circular position line of the base station in NLOS

图1中虚线圆位置线表示各个基站均处于LOS环境下的测距现象，此时目标可能存在的区域为图1中实线阴影部分，实线圆位置线表示基站4处于NLOS环境下的测距现象。若处于NLOS环境下简单的使用最小二乘算法进行定位解算，定位精度定会受 NLOS影响较大。针对该问题，提出了一种内交点定位算法(Interior intersection location algorithm, IILA)。通过计算各个圆位置线之间的交点，并建立几何约束条件对其进行筛选，最终实现目标位置的估计。即使少数基站存在较大的NLOS误差的环境下，该方法可将目标可能存在的区域缩小为图1中实线和虚线的阴影部分，确保较高的定位精度。

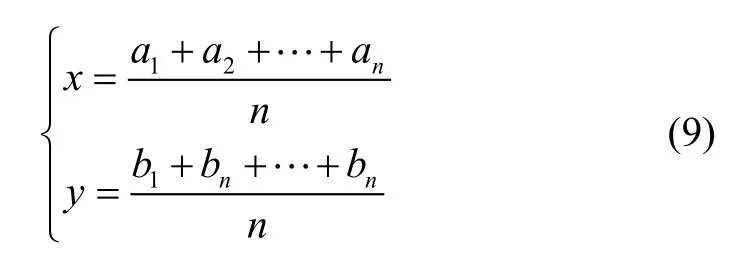
3 基于指数渐消记忆加权的测距滤波

由于无线信号的不稳定性，无线定位系统的定位结果容易产生跳变，减小信号的跳变有利于提高定位精度。指数渐消记忆加权法（Exponential fading memory weighting, EFMW）充分利用了每一组数据，采用指数衰减加权方式进行滤波，可在一定程度上缓解信号的突变。假设时刻信号的输出，时刻信号的输入，且输入和输出之间满足式(10)所示关系：

其中，

常有如式(12)所示因式分解：

因此，由式(8)和式(13)可知：

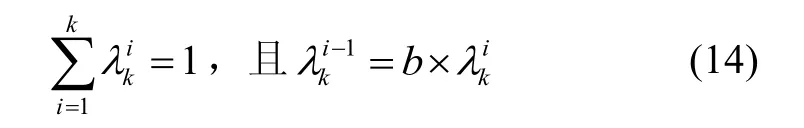
由式(11)中加权系数的定义以及式(10)可知，信号的输出由先前个时刻的输入决定，且先前数据的权重在以的指数次方衰减，故称此类加权算法为指数渐消记忆加权平均。该方法既发挥先前数据的价值，又强调新数据的作用，可有效减弱信号的突变。

联合式(10)和式(15)可得：

其中递推公式为：

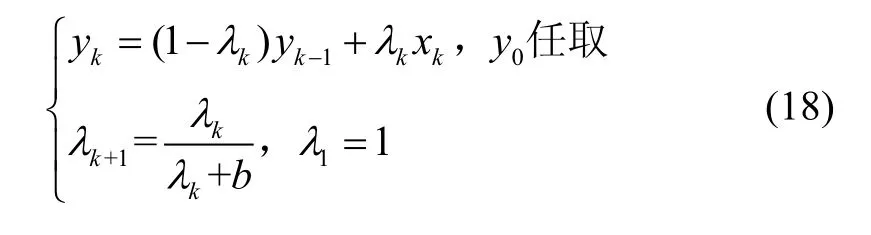
4 实验验证

为验证本文所提出的算法，采用Nanotron公司研发的基于线性调频扩频（CSS）定位原理的Nano定位系统进行实验，系统由4个基站和1个定位标签组成。选取了一间储物间作为实验场地，试验场景如图2所示。

图2 实验场景Fig.2 Test environment

4.1 测距滤波算法验证

依次将移动标签定点放置于9个参考点处，采集各个基站的测距数据。为了验证指数渐消记忆加权滤波算法，选取第9号参考点作为分析对象，其中渐消记忆因子设置为0.95。各个基站滤波前后数据对比如图3～6所示。由这些图可知，采用指数渐消记忆加权测距滤波算法可对基站测距信息进行有效滤波，减小了无线信号的跳变，可提高无线系统的定位性能。

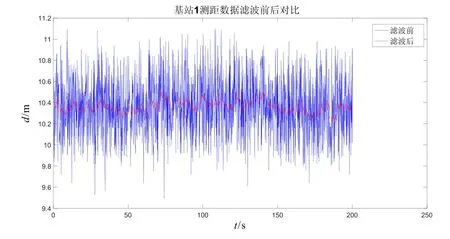
图3 基站1测距数据滤波前后对比Fig.3 Comparison on BS-1 range data before and after filtering

图4 基站2测距数据滤波前后对比Fig.4 Comparison on BS-2 range data before and after filtering

图5 基站3测距数据滤波前后对比Fig.5 Comparison on BS-3 range data before and after filtering

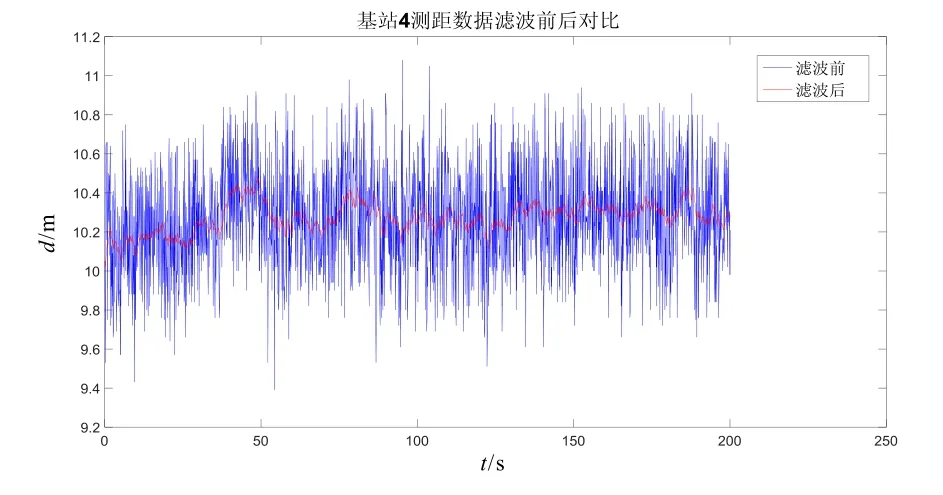
图6 基站4测距数据滤波前后对比Fig.6 Comparison on BS-4 range data before and after filtering

4.2 静态实验验证

为了验证内交点定位算法，分别对9个参考点采用不同的定位算法进行解算，计算每个参考点的均方根误差RMSE（m），计算结果如图7和表1所示。

图7 不同定位算法静态定位精度对比Fig.7 Comparison on static positioning accuracies of different location algorithms

表1 不同定位算法静态定位精度对比Tab.1 Comparison on static positioning accuracies of different location algorithms m

从图7及表1可知，采用迭代最小二乘定位算法，各参考点RMSE最大值为4.5216 m，最小值为0.3793 m，均值为2.1359 m。而采用本文提出的内交点定位算法各参考点RMSE最大值为1.8562 m，最小值为0.3040 m，均值为0.8596 m。尤其是参考点4，迭代最小二乘算法RMSE为4.52 m，而采用内交点算法RMSE 为0.41 m。

综上，采用本文所提出的定位算法，定位精度优于 2 m，定位精度有了明显提高，算法的环境适应能力更强。但是由于是静态实验，无线信号在均值附近的跳变基本呈现高斯性，因此目标位置解算之前利用指数渐消记忆加权法进行测距滤波，对于静态定位精度的影响不是十分明显。

4.3 动态实验验证

为了全面验证指数渐消记忆加权滤波的内交点定位算法，进行了一组动态实验验证。按照参考点1-2-3-4-5-6-7-8-1的顺序，采集了一个矩形路径的实测数据。分别采用4种不同的定位算法进行解算，结果如图8～11所示。

比较图8和图10以及图9和图11可以发现，内交点定位算法比传统的迭代加权最小二乘算法定位精度明显提高，环境适应能力更强。通过对比图8和图9以及图10和图11可知，指数渐消记忆加权测距滤波算法可以有效削弱无线信号的跳变现象，使得前后时刻的定位点离散程度减弱，连续性更强，目标运动轨迹图效果更好。比较图8和图11发现，采用传统的定位算法解算出的是一些杂乱无章的点，而采用本文提出的算法基本可实现矩形轨迹的复现。

图8 IWLS处理结果Fig.8 IWLS processing results

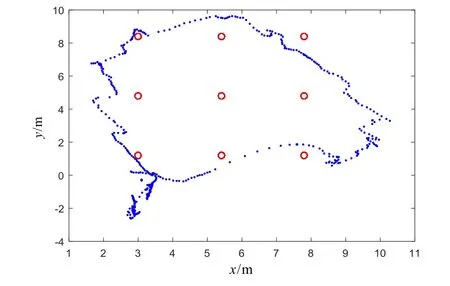
图9 EFMW+IWLS处理结果Fig.9 EFMW+IWLS processing results

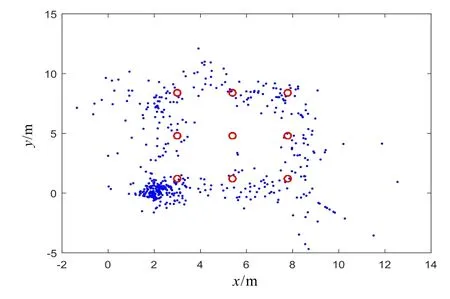
图10 IILA处理结果Fig.10 IILA processing results

图11 EFMW+IILA处理结果Fig.11 EFMW+IILA processing results

综上，采用指数渐消记忆加权滤波的内交点定位算法提高定位精度的同时，无线定位结果的跳变现象得到了明显的改善。

5 结 论

基于 TOA的无线定位系统是室内定位中常用的一种方法，但是一般的无线定位系统存在其固有的弊端，例如多路径、非视距、易干扰等，如何消除这些弊端对定位精度的影响，成为了当前迫切需要解决的问题。本文针对无线定位系统中存在的非视距传播这一关键误差因素，提出了一种内交点定位算法进行目标位置估计。该算法的优点在于无需识别视距环境还是非视距环境，无需利用任何先验信息，只需对多个基站圆位置线之间的几何关系进行处理，通过建立几何约束条件，实现对目标位置的估计。同时，为了减小无线定位系统信号跳变的影响，采用指数渐消记忆加权测距滤波算法，通过设置合适的渐消记忆因子调节测距信号的跳变幅度。

综上，指数渐消记忆加权滤波的内交点定位算法可以有效提高系统定位精度。同时，无线信号的跳变现象明显得到削弱，具有一定的实用性。