多层多源信息融合旋翼无人机测高算法
2018-08-27刘一恒
黄 鹤,刘一恒,赵 熙,许 哲,郭 璐
(1. 长安大学 电子与控制工程学院,西安 710064;2. 北京航空航天大学,北京 100083;3. 中电科第20研究所,西安 710068;4. 无人机系统国家工程研究中心,西安 710072)
无人机测控技术是指对无人机进行遥控、遥测、跟踪定位和信息传输,不仅体现在在较大空域条件下对飞机飞行状态和设备状态的控制,而且还需要对其参数进行测量,其中,准确的高度测量数据是复杂环境下低空自主飞行和悬停控制系统的必要输入条件[1]。机载测高传感器通常包括气压计、GPS、加速度计和无线电高度表等。大量试验表明:气压计数据连续且分辨率高,但受大气压力影响,测量误差随着高度降低而增大,难以满足测高精度[2-4];GPS定位准确度高,但其被动定位特性会使其具有较低的测量数据更新率,易受 GPS码型改变或系统关闭影响出现定位故障[5];加速度计可以测量高度方向的速度变化,短时间内具有高精度,但随着时间增长,高度变化量的误差会累积,致使测高数据发散;无线电高度表测量精度较高,通常装备在大型固定翼飞机和无人直升机上,获取飞机与地面或海平面的相对高度,受地形状况影响较大,应用范围有限,在地面海拔高度未知的情况下无法获取飞机的绝对高度,且四旋翼无人机载荷有限,一般不会装备。由此可见,以上各传感器受自身测量特性和应用场景的限制,依靠单一传感器很难满足无人机的高度精确测量需求。
针对上述问题,文献[6-10]中的学者研究了各类传感器的测量特性、数学特性,尝试将不同类型传感器进行信息融合。本文综合气压计、GPS和加速度计三种传感器的特点和信息数据资源,实现优势互补。无人机信息融合测高系统工作流程如图1所示。当系统中的个别传感器失效或出现故障时,可利用其它正常工作的传感器采集信息,综合计算获取量测信息,具有较强的容错性。同时,可充分利用多传感器协调和性能互补[11],依据设计的准则将多传感器的数据信息资源合理支配和使用,进行筛选、分析和处理,利用从不同信息源得到的在时间和空间上可冗余或互补的信息进行组合、推理和集成,以获得高度信息的一致性解释和描述,克服单一传感器的不确定性和局限性,提高整个系统的鲁棒性,全面准确的描述被测对象[12]。

图1 无人机信息融合测高系统Fig.1 AUV height measurement by information fusion
一步延迟时间融合算法是文献[13]提出的一种应用在雷达信号处理过程中的信息融合算法,本文首先将其引入应用在无人机测高过程中,但精度提升有限。针对这个问题,提出了一种多层多源信息融合悬停旋翼无人机测高算法,应用在悬停状态的无人机测高过程中。首先提出一种基于二步延迟自适应时空算法,作为第一层融合,对气压计和GPS测得的历史数据进行处理,提升融合精度。将基于参数辨识的自适应互补滤波用于第二层融合,利用加速度计数据的辅助测高,组建多步时空双重融合模型,相对于一步延迟融合方法,进一步提升旋翼无人机测高数据的准确性。
1 多传感器测高模型
1.1 气压计
气压计是利用大气气压会随着高度的增加而降低的原理来测量高度。以标准海平面作为基准面,当高度在11 km以下时,标准气压高度公式为:
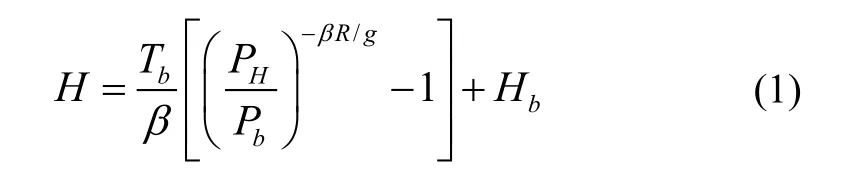
式中:PH和Pb分别是高度为H和Hb时对应的气压(Pa);Tb是高度为Hb时的温度(K);β是温度垂直变化率(K/m);R是空气专用气体常数(m2/k·s2);g是重力加速度常数(m/s2)。气压计测高模型为:

式中:h1是气压计的测量高度;h是真实高度;ε1是气压计测量噪声。
1.2 GPS
GPS测高可以得到无人机在WGS-84坐标系中的准确位置,经过坐标系转换,可以求得大地高HG,即以椭球面为基准时无人机的高度;实际测量需要正常高H,它是以似大地水准面为基准测得的高度;椭球面和似大地水准面之间的高度差称为高程异常ξ。它们之间的关系可以表示为:

GPS测高模型为:

式中:h2是GPS的测量高度;h是真实高度;ε2是GPS测量噪声。
1.3 加速度计
加速度计可以测量出无人机高度方向的速度变化,通过对速度积分,短时间内可以得到精度较高的高度变化量,但长时间会使误差累积,最终导致测高数据发散。无人机相对地面的高度H、垂向速度Vg和垂向加速度ag之间的关系为:
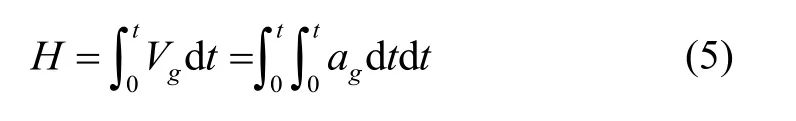
加速度计测高模型为:

式中:h3是加速度计的测量高度;h是真实高度;ε3是加速度计的测量噪声。
由此可见,各类传感器检测结果受到自身测量特性的限制,无法满足无人机对高度的精准测量要求。本文算法从气压计、GPS和加速度计的测量特性出发,进行高度测量信息的融合,达到精确测量的目的。
2 一步延迟时间融合算法
文献[8]提出了一步延迟时间融合算法,主要应用在雷达信号和数据过程处理中,通过递推估计实现单一雷达传感器在不同时刻的融合估计,减小或者消除其在测量过程中的不确定性,通过前后时间邻域点测量数据的重复运算,提升结果的正确率,获取可靠性更高的测量数据。
设采用多传感器(个数为d)对某一被测参数进行测量,在某一时间间隔内,每个传感器测量到n个数据Zi(1),Zi(2), …,Zi(n),i=1, 2, …,d,然后采用时间融合估计。对于真值X,第i个传感器前两个时间点测量可得:
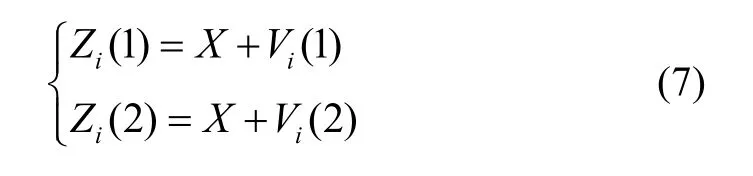
V1(1)、V1(2)为符合正态分布的测量噪声,假定其均值均等于零,方差分别为δi2(1)、δi2(2)。假定X、V1(1)、V1(2)都是相互独立的随机变量。第1个时间点采用同一传感器获取X估计值的均值和方差:

利用时间递推估计理论推出第2个时间点的最优估计值Zi+(2)和方差Pi+(2)为[8]:
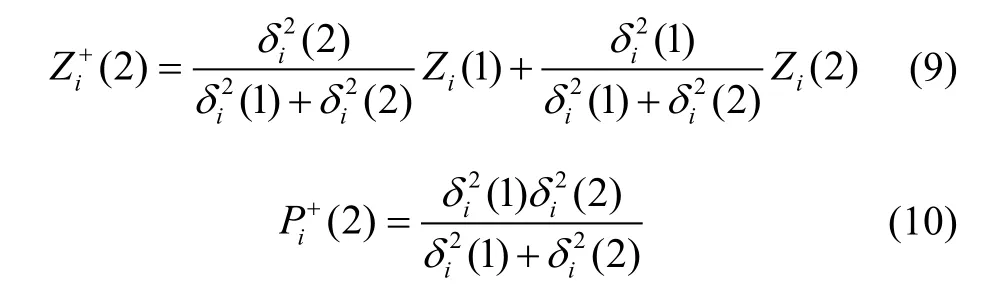
传感器采集高度的量测数据后,将每次估计值Zi+和方差Pi+作为下一次采集测量的统计特性,将新的测量数据用于修正依次递推计算。可得同一传感器k次测量后的时间融合估计值Zi+(k)和方差Pi+(k)为:
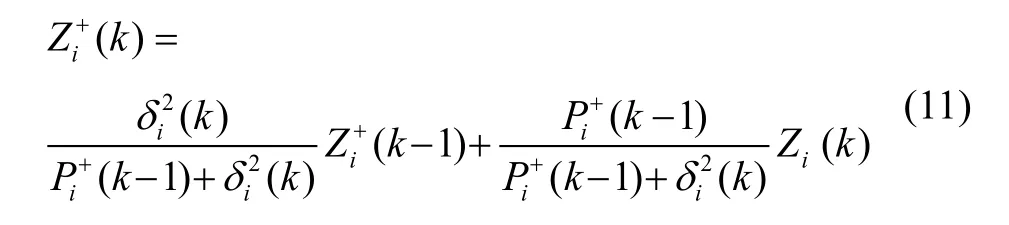

在此基础上,测量方差可以通过单一传感器的自协方差因子和互协方差因子计算获取。
3 多层信息融合无人机测高算法
3.1 多层信息融合总体框架
本文设计的无人机测高信息融合模型由两层组成,其系统框架如图2所示。第一层为二步延迟时空融合,包含二步延迟时间融合和空间融合两个子层。第二层为基于参数识别的自适应互补滤波。

图2 多源多层融合系统框图Fig.2 System diagram of multi-layer and multi-source information fusion
通常情况下,气压计和GPS的噪声较大,长时间工作时,其数据较为稳定,能够保持在高度真值附近波动。加速度计的噪声较小,经过两次积分,可以转化为位移,在短时间内较为精确,但开机时间长了,会产生积分漂移,误差较大,因此仅仅设计一层时空融合算法是不够的,无法将加速度计数据与气压计和GPS数据同时进行融合。这里必须要另外设计一层信息融合方法,实现加速度计的辅助测高,在较长时间工作条件下,用GPS和气压计的时空融合值对加速度计的积分值进行缓慢的修正,抑制积分漂移现象。这里第二层信息融合采用互补滤波。在做第一层信息融合过程中,当GPS和气压计的数据噪声较大时,时空融合算法计算出的融合高度数据会出现一些尖锐的毛刺,当其进入到滤波后的波形中,将会使无人机的高度数据产生误差,而采用常规互补滤波算法无法彻底滤除这些毛刺。针对这个问题,本文设计了一种基于参数识别的自适应互补滤波算法,应用在第二层融合中。
3.2 第一层融合
在第一层融合过程中,结合无人机测高过程中数据量较小的特点,设计一种新的采用基于二步延迟自适应时空融合的融合算法,采用更多的历史数据完成数据融合估计。
该算法首先利用高度传感器在某一时间点的量测值与前两个时间点的估计值进行融合,可计算得到同一传感器在多时间点的融合估计值,然后将各异类传感器同一时刻的估计值进行空间融合,从而得到最终的估计值。通过两个子层的划分将数据融合分解为两次估计——基于二步延迟时间的最优融合估计和基于空间的最优融合估计。这两个子层构建的数据融合算法不需要先验信息,利用采集获取的观测数据精度来确定其对应的不同权值,从而计算出均方误差最小的融合值。第一层融合过程如图3所示。

图3 第一层融合框图Fig.3 Fusion process of the first layer
在高速数据量测过程中,在无人机的不同空间位置装备d个异类高度传感器,各个传感器在不同时间和空间所获取的无人机高度观测数据是不相同的。d个传感器在n个不同时间点的工作期间获取高度值会出现d×n个观测值。第一层信息融合分为两个子层,第一子层是在一步延迟时间融合估计基础上推导基于二步延迟时间的递推估计融合估计,将各个传感器分别进行基于两个时间点延迟的高度数据的融合估计,通过结合历史数据的修正消除每个传感器依据时间获取观测数据的不确定性,提升单传感器量测数据的精度和可靠性,将实时测量的高度数据进行第一步处理;第二子层将各个单传感器处理后的高度数据进行自适应加权融合估计,实现高度数据多传感器的空间融合。在此阶段,每个传感器所得到的同一时刻的估计值在完成了时间融合估计后,自适应确定最优加权系数,使该时刻获取的高度数据值的总均方差达到最小,从而实现最优估计。分两个阶段进行信息融合是为了采用更多的观测值集合Z,实现二步延迟时空融合,从而得到更精确的高度数据。
3.2.1 第一子层二步延迟时间融合
设无人机测高过程中共有d个高度传感器,在某一时间间隔内,单个高度传感器获取n个量测数据,即Z1(1),Z1(2), ...,Z1(n),i=1, 2, ...,d,也就是说Zi(k)是第i个高度传感器在k时间点的高度数据量测值,即观测值Z={Zi(k)}(i=1, 2, ...,d;k=1, 2, ...,n)。首先,进行第一阶段单个传感器二步延迟高度信息时间融合估计,假设第i个传感器获取数据时,高度真值为X,前两个时间点获取的高度数据测量结果与公式(7)相同,单个高度传感器在某一时间点测量之后计算出的X估计值的均值和方差与公式(8)相同。
通过二步延迟时间融合,推导出第3个时刻点测高的估计值和方差:

分别采用前两个时间点的估计值和相应的方差作为历史数据,进行单传感器时间二步延迟融合计算。在计算过程中每一传感器同一次只采用一个高度测量数据,将某一个点估计值及其方差作为下两个时间点高度测量数据的统计特性参与计算,这样每次估计值的求取都会用到本次的测量数据和前两次的估计数据以及本次的方差和前两次的方差。以此类推可得k次测量后单一测高传感器融合估计和方差为:

单个高度传感器每次测量方差为δi2(k),可以通过高度传感器的自协方差参数和互协方差参数的差算得。为了简便计算,这里设有任意两个不同传感器p、q,其高度测量值分别为Xp(k)、Xq(k),其测量误差分别为Vp、Vq。p的自协方差为Rpp,p与q的互协方差为Rpq。通过时间域估计公式,可以得到:
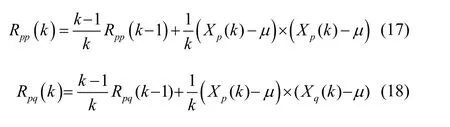

其中,μ为采样数据均值。
3.2.2 第二子层空间融合
通过式(15)(16)可得d个传感器第k次测量估计值Z1+(k),Z2+(k), …,Zd+(k),均方误差值P1+(k),P2+(k), …,Pd+(k),以及加权系数W1(k),W2(k), …,Wd(k)。利用图4空间融合方法,计算可得异类传感器空间最优融合结果Z*(k)为:

由Z1+(k),Z2+(k), …,Zs+(k)相互独立,得第k次多传感器测量时空融合总均方误差为:

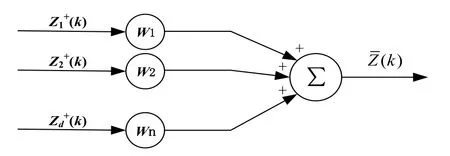
图4 空间融合过程Fig.4 Space fusion process
δ2(k)是二次函数,利用加权系数W1(k),W2(k), …,Wd(k)满足约束条件的多元函数极值求取δ2(k)的最小值,得到最优加权系数为:

最终总的均方误差为:

由公式(23)可见,在第二阶段进行多传感器自适应加权空间融合后,获得的均方误差比单一传感器采用二步延迟时间融合估计所获得的均方误差Pi+(k)更小,精度更高。基于空间最优融合估计算法所得的均方误差则:

通过式(24),δi+(k)作为δi(k)的估计值,其值大于δmin(k)。因此,结合式(17)~(24)可以得到即自适应加权两级融合算法均方误差相对于基于空间融合有一定的减小。也就是说,经过了第二阶段自适应加权空间融合处理后,均方误差变小了,相对于基于单个传感器的时间融合或多传感器的空间数据融合,其数据精度都有所提升。
3.2.3 计算步骤
以两个传感器测量数据样本的融合估计为例,基于二步延迟的时空估计算法的计算步骤如下:
(a) 进行第一阶段融合,利用公式组(17)~(20)进行计算,获取测高传感器采样时间点Rpp(k)、Rpq(k)、Rqq(k)、Rqp(k),通过计算可以得到测高采样时间点的δp2(k)、δq2(k);
(b) 分别将两个传感器的第一次测量值Zp(1)、Zq(1)和方差δp2(1)、δq2(1)作为系统初始参数,利用公式(5)计算得出每个测高传感器采样时间点基于二步延迟的时间融合估计值Zp+(1)、Zq+(1)和对应的融合方差Pp+(k)、Pq+(k);
(c) 进行第二子层空间融合,利用公式(15)计算得到采样时间点各个测高传感器的最优加权系数Wp(k)和Wq(k);
(d) 利用公式(20),获取基于二步延迟时空融合估计结果Z(k)。
3.3 第二层融合
在第二层融合过程中,设计了一种基于参数辨识的自适应互补滤波算法,其融合过程如图5所示。

图5 第二层融合过程Fig.5 Fusion process of the second layer
通过该算法进行第二层融合,实现加速度计的辅助测高,在长时间工作状态下,用GPS和气压计的时空融合值对加速度计的积分值进行缓慢的修正,抑制积分漂移现象。具体公式如下:

其中,v是垂直速度,a是垂直加速度,x是垂直位移,z是GPS和气压计时空融合的结果,T是时间常数,e是每次的修正量,k是自适应系数(开关量,只取 0和1),F是最终的融合结果。
融合过程中,T是可调节的参数。当T大时,更多地信任加速度计积分;而当T小时,更多地信任时空融合的结果。k的取值由修正量e决定,当e绝对值大于所设阈值时,k取0,否则,k取1,实现了对参数e的辨识,这样就过滤了极端值,因为x在短时间内是精确的,如果e过大,则证明z的取值不正常,此时,不把错误的e加进积分中,使波形参照加速度计的积分波形,不会出现大的波动,这样就实现了互补滤波的自适应性。
4 实验结果
为了验证本文算法的有效性,实验采用某无人机在240 m高空悬停时的实测数据,进行计算机仿真分析,气压计和GPS测量值如图6~7所示。正如2.1节分析,测量误差较大,围绕240 m上下波动,但结果比较稳定。
本实验采用三轴MEMS数字加速度计MPU6050。先放置在水平桌面上,Z轴朝下,对X、Y轴进行零位校准;然后绕X轴旋转90°,对Z轴进行零位校准;校准之后,对所测得的数据先进行卡尔曼滤波,得到静止状态下Z轴的数据为Zg(Zg表示静止条件下重力加速度g对应的数据,为负数)。

图6 气压计测量曲线Fig.6 Measurement data of the barometer
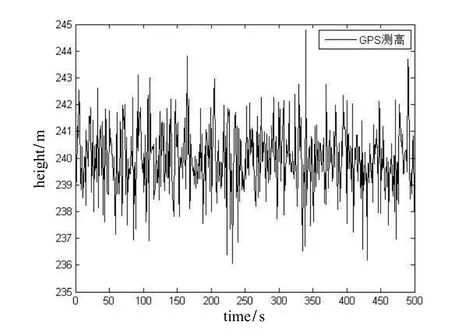
图7 GPS测量曲线Fig.7 Measurement data of the GPS
在进行实验时,将实时获取的加速度计Z轴数据与Zg作差,得到无人机垂直向加速度。加速度计的测量数据如图8~10所示,误差相对比较小,但稳定性不够,工作时间过长会产生积分漂移,需要其他传感器测高数据做修正。
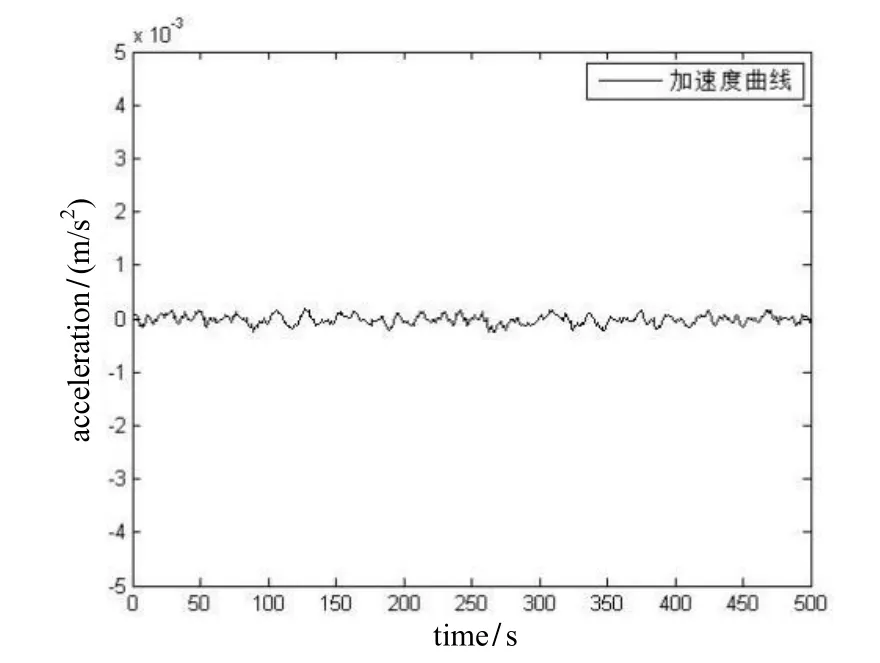
图8 加速度计的加速度测量值Fig.8 Acceleration measurement of the accelerometer
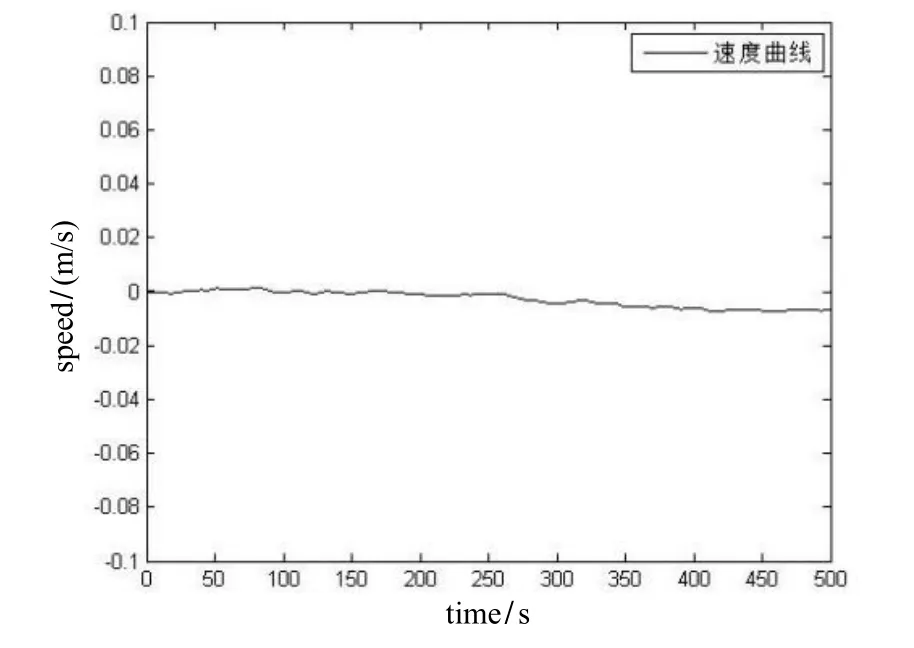
图9 加速度计的速度估计曲线Fig.9 Estimation speed of the accelerometer

图10 加速度计的测量高度估计曲线Fig.10 Estimation height of the accelerometer
图11~12为采用气压计测高数据进行的一步延迟时间融合算法和二步延迟时间融合算法的误差。结合表1(表1数据更直观)和这两张结果图可以看出,二步延迟时间融合可以进一步减小均方误差,这是由于计算过程中采用更多的历史数据计算的原因。同时,测高刚开始的一段时间会产生大噪声,也就是最大误差,二步延迟时间融合算法有明显改善。
图13为多层融合误差曲线,图14为多种误差对比图。结合表1可知,在进行第二层融合之后,相比于一步延迟融合方法,高度估计值的均方根误差减小43.6%,最大误差减小53.6%,精度得到了大幅度的提升。

表1 实验结果评价指标Tab.1 Evaluation of experimental results

图11 气压计一步延迟时间融合算法误差Fig.11 Barometer’s measurement error of the 1 step delay fusion algorithm
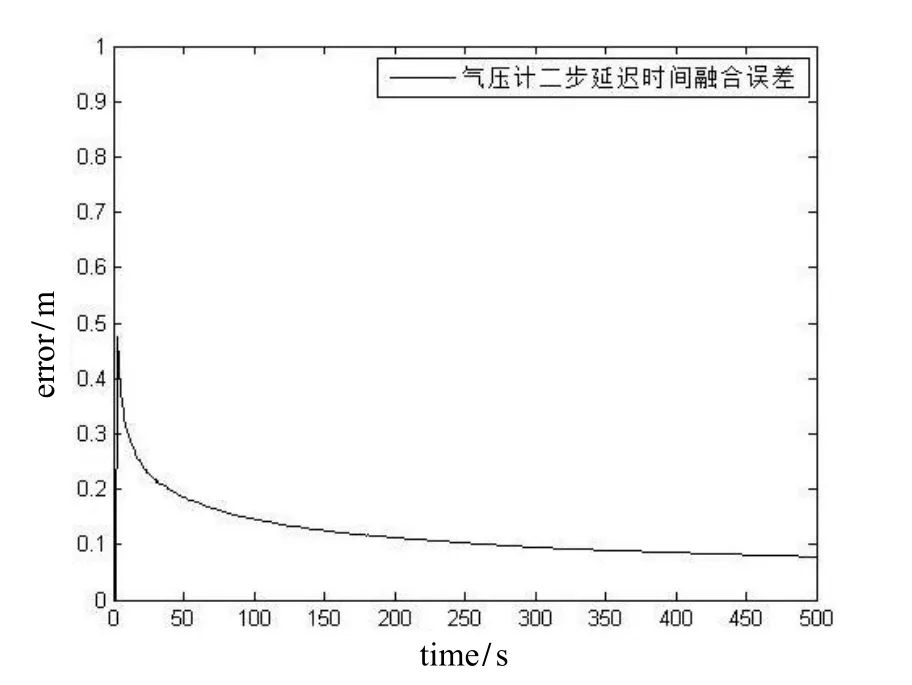
图12 气压计二步延迟时间融合算法误差Fig.12 Barometer’s measurement error of the 2 steps delay fusion algorithm

图13 多层融合误差曲线Fig.13 Measurement error of the multiple layer fusion
5 结 论
本文设计了一种基于多层多源信息融合的无人机测高算法,包含基于二步延迟自适应时空的第一层融合和基于参数辨识的自适应互补滤波的第二层融合,以克服现有技术存在的缺陷。
在借鉴雷达信号处理基于一步延迟自适应时空融合算法的基础上,结合无人机测高过程中数据量不大的特点,实现了多步时间和空间双重融合模型。采用更多的历史数据完成数据处理,使融合精度更高。进行基于参数辨识的自适应互补滤波第二层融合,实现加速度计数据的辅助测高,使旋翼无人机在飞行和悬停过程中测高数据更加准确,保证飞行和任务执行的稳定性。同时,该算法总的计算量并不大,编程简单,在硬件上不需要额外的设计,使系统在保证高可靠性的同时兼顾经济效益,是一种低成本、高准确度和可靠性的旋翼小型无人机高度测量方法。
