双轴旋转调制惯导系统的极区导航算法

张崇猛，项 铮，李 杨，孙伟强

（1. 天津航海仪器研究所，天津 300131；2. 海军装备研究院，北京 100161）

极区具有重大的经济和战略价值。北极地区的油气资源储备非常丰富。根据美国地质调查局的相关资料显示，全球待开采的油气资源总量中，有25%都分布在极区，其中原油储量占 20%，天然气储量占40%[1]。而极区冰面据相关资料显示，正以约每10年9%的速度消失，预计将在2060～2080年间完全融化，融化后亚欧美洲之间的航线能够缩短8000多千米，北极航道将成为连接大西洋和太平洋的最短的航道。但是由于北极地区的独特地理位置与环境，舰船在极区使用卫星导航[2]、 地磁导航[3]等导航方法时，都会存在一定的问题，无法正常输出导航信息。

由于信息的隐蔽性和自主性，惯性导航已成为舰船在极地区域导航的首选[4]。文献[5]提出了一种载体运动隔离算法，通过隔离载体运动并使用旋转调制技术能够很大程度上调制惯性元件的误差（陀螺漂移和加速度计零偏）对惯性导航系统性能的影响，减缓了惯性元件发展水平对于导航系统精度的制约。文献[5]中使用了传统的固定指北坐标系导航方法，其航向以经度线为参考基准，选择经纬度坐标来表示位置信息，但在北极地区，经线会急剧收敛至极点，导航设备不再能保精度运行。为解决平台施矩的问题，文献[6]提出采用游移与自由方位机械编排方法的惯性导航系统，但使用传统的导航参数导出方法时，游移方位角与自由方位角在极点附近会失去定义，同时，解算误差也会随着靠近极点而迅速增大。文献[7]提出了横向导航的概念，建立了横向地球椭球模型，并对横向经纬度进行了定义，使用固定指北机械编排方法解决了舰船在极区航行时存在的导航失准的问题。

鉴于上述文献的学术成果，本文提出一种将游移方位坐标系作为导航坐标系的旋转式惯性导航系统，其导航编排在横向地球坐标系下进行。舰船在极区外其他区域航行时，把姿态参数和速度参数投影到传统地理坐标系中，使用传统经纬度表示位置参数；而航行至极点附近区域后，转为使用横地球模型，确定游移方位角后，把姿态参数和速度参数投影到横地理坐标系中，使用横经纬度表示位置参数。通过这种方式，系统能够保持统一的导航坐标系，并能有效地实现在极区稳定的导航。

1 定义坐标系及经纬度

1）惯性坐标系Oxi yi zi(i系)：将地球的中心设置为坐标系原点，把x轴的指向设置为春分点，z轴重合于地轴，y轴与x轴共同构成右手直角坐标系。

2）地球坐标系Oxe ye ze(e系)：将地球的中心设置为坐标系原点，坐标轴静止于地球，在赤道平面内x轴相交格林威治子午线，z轴重合于地轴，可通过右手法则确定y轴。

3）地理坐标系Oxt yt zt(t系)：将坐标系原点设置为P点（载体的质心），三个坐标轴x轴、y轴和z轴分别指向东向、北向和当地垂线的向上方向。

4）载体坐标系Oxb yb zb(b系)：该坐标系固联于载体上，属于正交坐标系，会跟随运载体的运动而运动。

6）构建横经纬网：建立横向地球坐标（即横经纬度），如图2所示。定义赤道与90oE的交点为横北极点，相应地，赤道与90oW的交点为横南极点，180o与0o经线构成横向赤道，北半球的90oW与90oE经线共同构成横向本初子午线，横经度和横纬度分别用表示。

图1 地理坐标系和地球坐标系Fig.1 Geographic coordinate system and terrestrial coordinate system

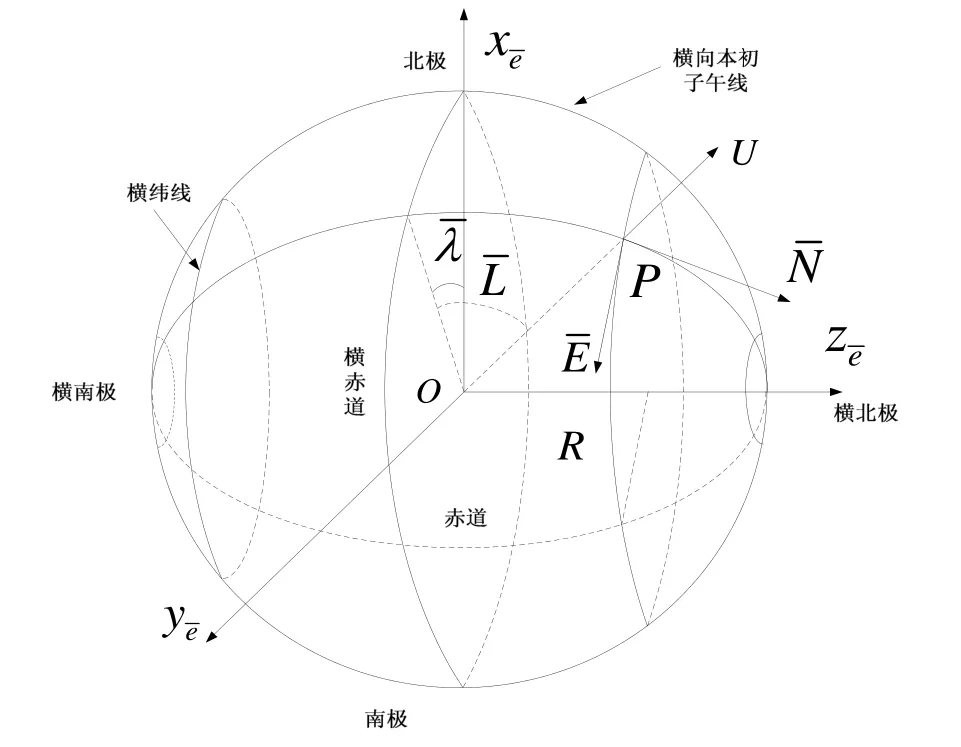
图2 横经纬网与横向坐标系Fig.2 Horizontal longitude and latitude network and transversal coordinate system

2 使用传统导航方法在极区工作的缺陷

传统的双轴惯性导航系统的结构框图如图3所示。

舰船惯性导航系统通常采用半解析式系统的方案，需要跟踪当地地理坐标系，当舰船航行到极区附近时，尤其在跨越极点的航行过程中，平台的y轴为保持指向真北方向需要迅速转动[10]。这样一来在航行至极点附近时，舰船的航向会迅速旋转180°，系统输给方位轴陀螺的施矩量此时会变得非常大，具体方向变化情况如图4所示。

图3 某型惯性导航系统结构框图Fig.3 Structure diagram of an inertial navigation system

图4 通过极点时载体的真北方向变化Fig.4 Orientation of true north at geography pole

在固定指北方位系统中有：

其中，VE和VN分别为传统地理坐标系上东向速度和北向速度投影，RN和RM分别为地球沿卯酉圈和子午圈的曲率半径，W为地球自转角速度。由式(1)可见，在地理极点即L=90o的附近区域，计算时会出现计算溢出的现象，还会伴随出现对惯性导航系统方位陀螺的施矩困难和系统误差被放大等情况，可知在极区，传统指北方位系统的导航算法无法正常工作[11]。

而在游移方位惯性导航系统的机械编排中，方位轴陀螺无需施矩，故可以解决当地水平指北方位惯性导航系统在纬度较高的极区工作时遇到的部分问题。游移方位角的数学模型如下：

由式(2)可以发现，在地理极点附近，没有了北向基准，游移方位角会失去意义，这使得游移方位惯性导航系统无法正常工作[12]。

通过理论分析发现，采用了当地水平坐标系为参考坐标系的固定指北方位及游移方位惯性导航系统机械编排方案，在地理极点处，惯性导航系统均会失去北向基准，可知在该参考坐标系上的任何导航方案都无法避免该问题的出现[13]。

所以，如想从根本上解决惯性导航系统在极区存在的失去北向基准、系统精度由经线圈迅速汇聚而下降等难题，需要对经纬度和北向重新定义，即建立新的导航参考基准。

3 基于横向游移坐标系的极区机械编排

通过两次旋转可以将传统地球坐标系转为横向地球坐标系，转动角度两次都是90-o，如图1图2所示，其旋转关系可以表示为：

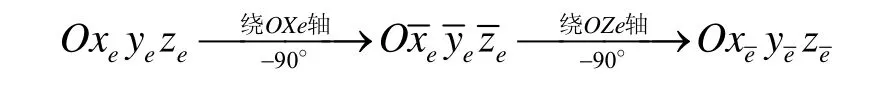
则传统地球坐标系与横向地球坐标系间的关系为：

经纬度与横经纬度的关系为：

与传统地理坐标系一样，横向地理坐标系也是当地水平坐标系，二者间存在一个沿当地地理坐标系z轴方向的夹角，设为角p，横向地理系与传统地理系之间的变换矩阵可表示为：

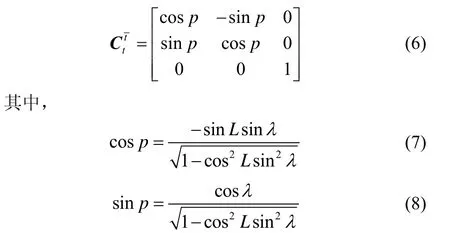
游移方位惯性导航系统跟踪当地水平面以及地球自转角速率，将其水平轴相对横向地理坐标系的夹角定义为横向游移方位角b，该角度不断变化。定义a为传统地理系下的游移方位角，逆时针方向为正方向，Yh为载体的航向，H为平台航向角，y为传统航向角，为横向航向角。这些角度在两个坐标系下的关系如图5所示。

设横向游移方位角的初始值为：

横向地球坐标系与横向地理坐标系间的变换矩阵为：

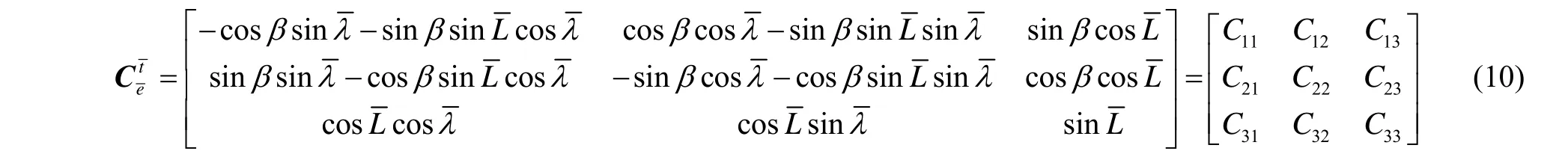
则：

的真值按表1确定。

方向余弦矩阵的微分方程为：

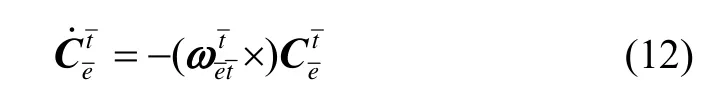
通过式(12)对方向余弦矩阵进行更新。横向游移方位角的微分方程为：

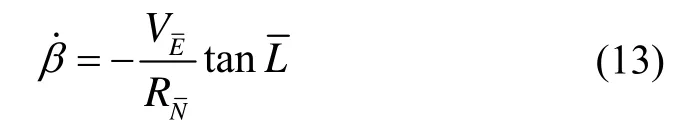
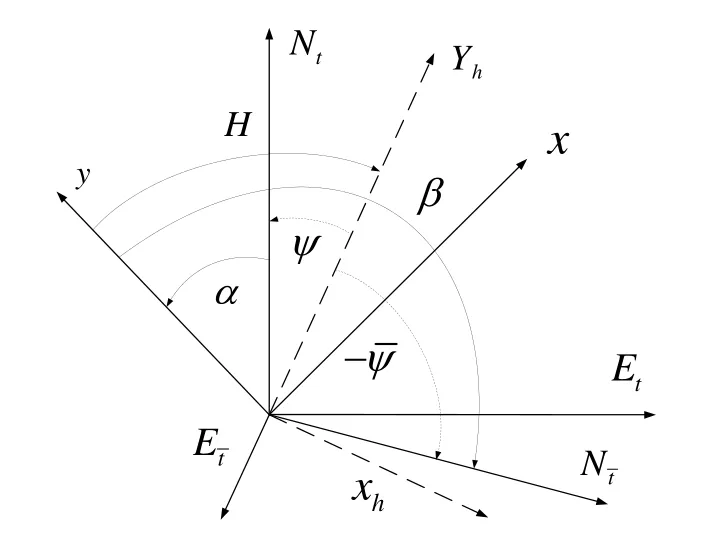
图5 传统与横向地理坐标系下的航向角、平台航向角和游移方位角Fig.5 Heading angle, flight angle and wander angle of traditional or transversal earth coordinates

表1 的真值确定Tab.1 Determining the true value of

表1 的真值确定Tab.1 Determining the true value of

C31l主为正 l主为负+ll=主ll=主ll=+oll=-o-主180主180

则：

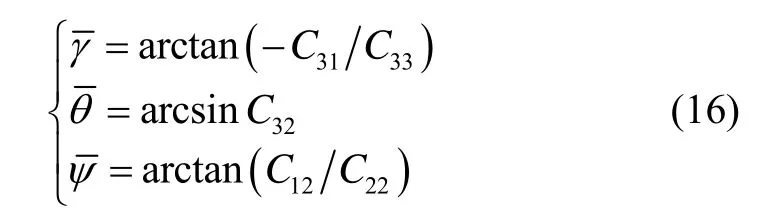
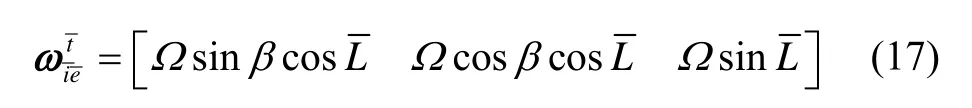
由于舰船航行时，水平速度远大于垂直速度，所以忽略掉垂直速度对舰船的影响。水平速度方程为：

R为横向坐标系下的曲率半径：

其中，f≈ 0.082为椭球扁率，为地球半长轴。

4 导航切换流程

在低纬度地区，使用传统地球坐标系下的机械编排方案进行导航，当舰船航行进入极区后，转换为使用基于横向坐标系的惯导机械编排方案。

在舰船进出极区的过程中，需要对导航信息进行转换。使用游移方位坐标系作为导航坐标系，传统地球坐标系与横向地球坐标系下的航向角和游移方位角在导航切换时的转换关系如下所示[14]：

在初始化的时候，首先获取IMU的导航坐标系的初始参数，然后同时采用传统地理系和横向地理系下的机械编排方案进行导航解算，最后在输出解算结果时对舰船的位置进行判断，当舰船进入极区时输出横坐标系下的导航解算结果，否则输出传统坐标系下的导航解算结果。这样做使得船舶在航行的过程中，不需要设计繁琐的导航坐标系切换逻辑，只需在输出解算结果时进行判断，避免了导航解算前加入逻辑判断对程序正确运行带来的影响，能够简化整个导航解算的算法流程。具体导航流程如图6所示。

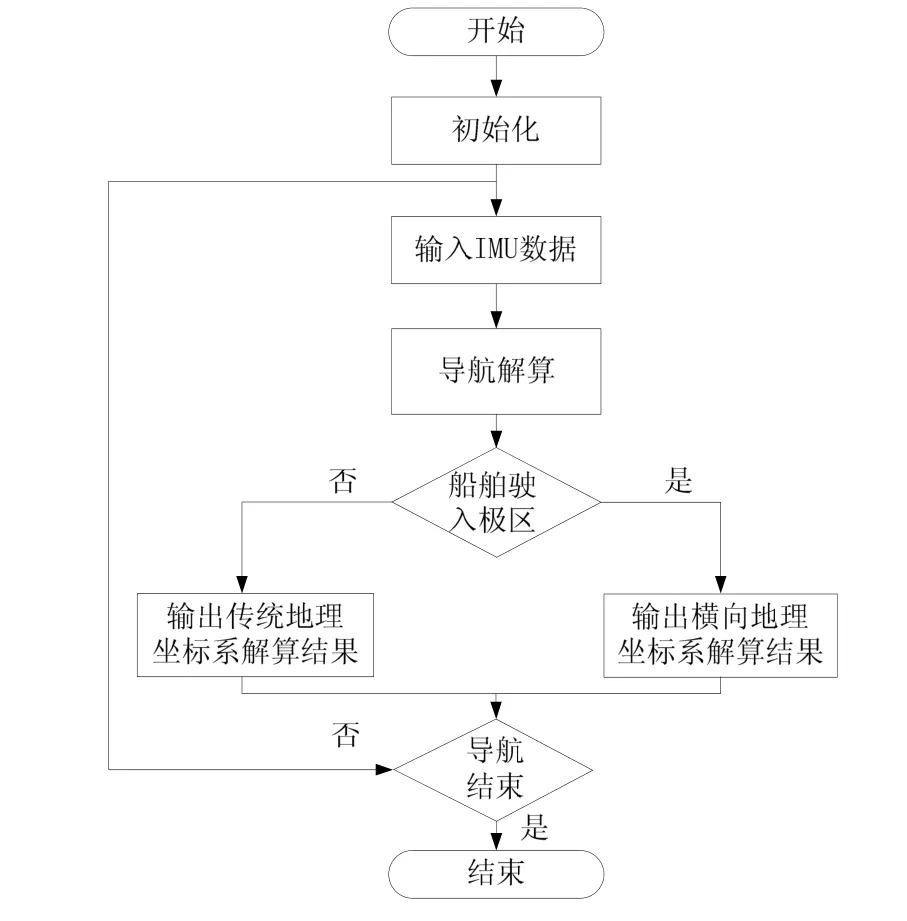
图6 导航切换流程图Fig.6 Navigation switch flow chart

设L1为从高纬度的极区到低纬地区的切换纬度，L2为从低纬到极区的切换纬度，设置二者为不同的纬度值，可以避免载体处于极圈临界位置时的频繁切换参数的问题[15]。本文设定L1=82°，L2=84°。

5 仿真分析

对双轴旋转式惯导系统进行仿真分析，使用十六次序转位调制方案。仿真初始条件设置为：转速为12 (°/s)，在每个位置停留时间为30 s，初始位置为[78°, 0°]，沿经线圈向极点航行，初始航向角为0°，载体的北向速度设为10 kn，东向速度为0，仿真时间设置为72 h，当纬度大于84°时判定为进入极区（仿真时间约为40 h）。

惯性元件参数设为：三个陀螺的零偏值均为0.002 (°)/h，三个加速度计的零偏值均为10 μg。

图7 固定指北机械编排的误差曲线Fig.7 Error curves of north-oriented mechanization

由图7可以看出，进入极区后，传统指北方位机械编排航向角误差与经度误差均迅速增大，在靠近极点附近时出现了发散现象。

使用游移方位坐标系后，如图8所示，没有解决传统固定指北机械编排的问题，且在极点附近游移方位角失去定义，也出现了比较大的误差值。这些试验结果验证了当设备使用传统惯性导航机械编排方法时，无法在极区正常工作。

图8 游移方位机械编排的误差曲线Fig.8 Error curves of wander mechanization

图9为以游移坐标系为导航坐标系的横向坐标系的误差情况，载体72 h航行后的经度误差约为0.45′，纬度误差约为0.08′，航向角误差约为0.1′，另外当舰船通过极点时，横坐标系惯导系统可以保精度工作，说明横向坐标系可以满足极点附近的航行要求。

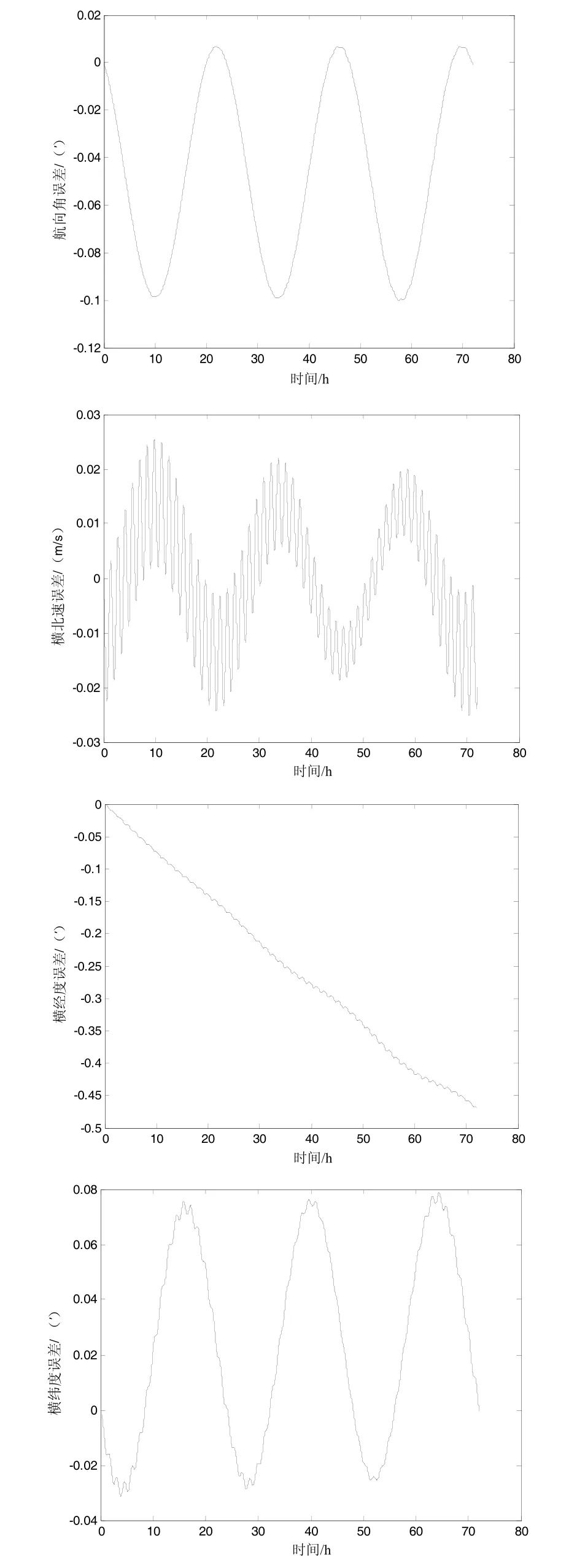
图9 横向坐标系的误差曲线Fig.9 Error curves of transverse coordinate system

6 半实物仿真验证

下面利用跑车试验得到的试验数据进行半实物仿真验证横坐标系极区导航方案的可行性。通过虚拟极区技术[16]，将双轴旋转式惯导系统的跑车试验数据转换为在极区下的航行数据。使用本文提出的横坐标系游移式惯性导航机械编排方案进行解算，构造虚拟极区的过程中，设置虚拟极点为GPS在第15 h的位置点，坐标为[39.21°, 117.175°]。离线工作24 h，利用GPS经纬度作为位置基准，把航向基准设置为惯导与GPS组合之后得到的航向，其试验路径如图10所示。

在转换为虚拟极区后，使用传统坐标系惯导机械编排方法时，惯导系统误差曲线如图11所示。

图10 跑车试验路径Fig.10 Test path of hardware-in-loop test

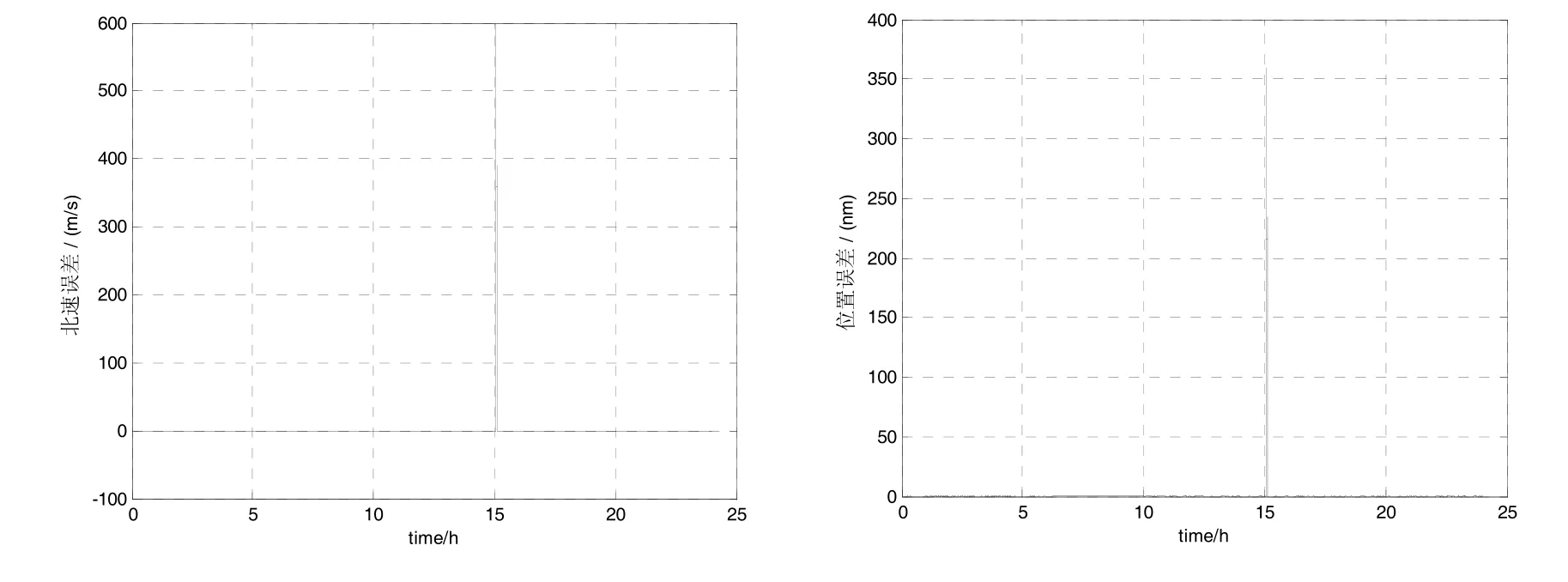
图11 传统坐标系的误差曲线Fig.11 Error curves of the traditional coordinate system

由图11可见，在极点附近惯导系统的速度误差和位置误差解算均出现了计算奇点，系统无法正常工作。

采用横向坐标系进行导航解算后，系统的横北速误差曲线如图12所示。

为了考察横向坐标系定位精度，可以将横向坐标系下的位置与GPS位置转换为横向坐标系下的位置相比较，得到横向坐标系位置解算误差，将该误差和系统在传统坐标系下解算的位置误差相比较，如图13所示。

可见二者误差曲线基本一致，能够说明横向坐标系解算方法的正确性。

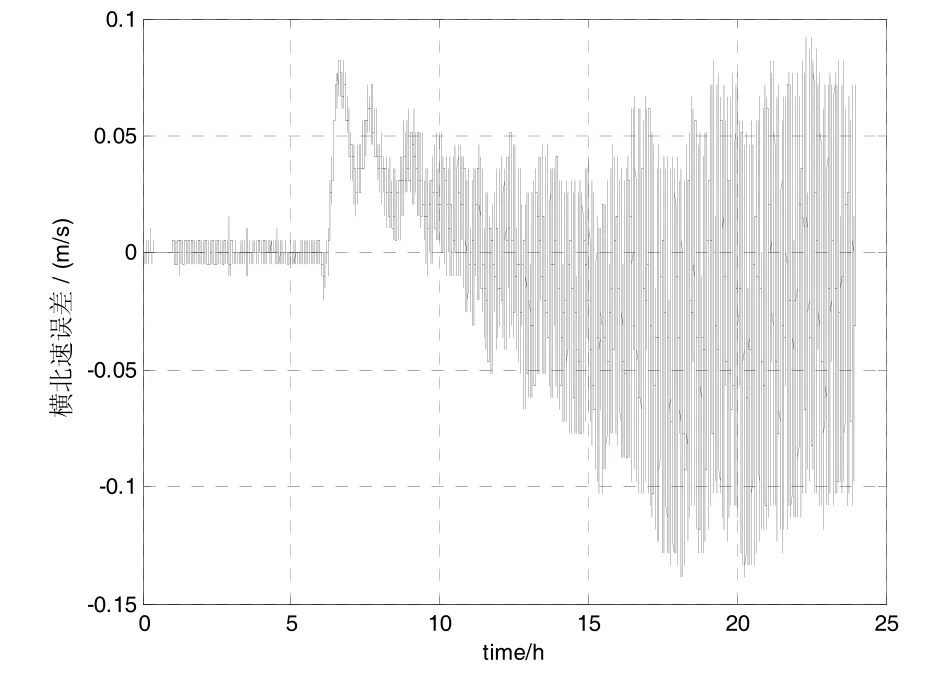
图12 横向坐标系的速度误差曲线Fig.12 Velocity error curve of transverse coordinate system

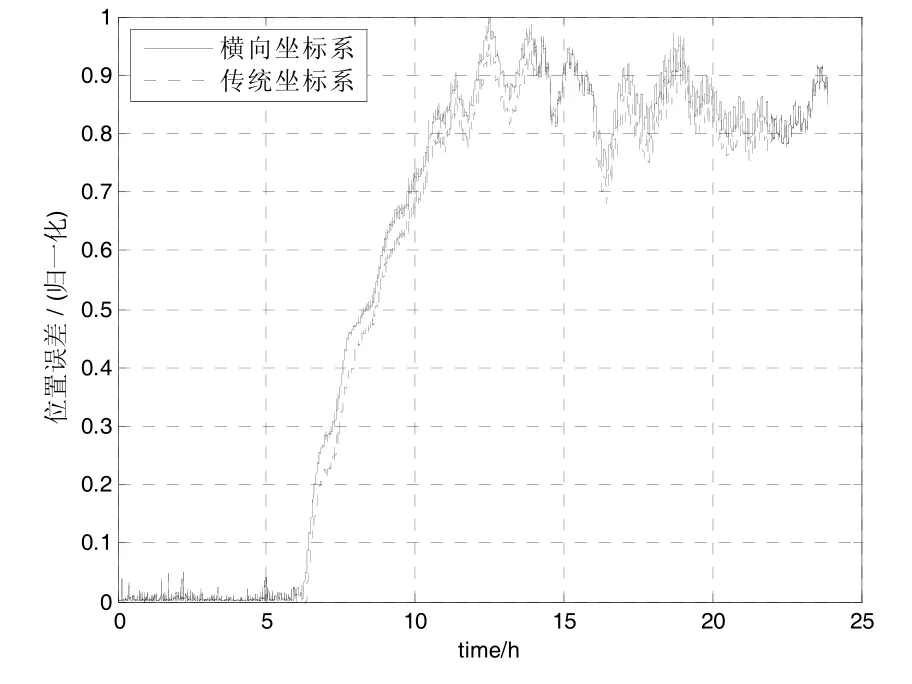
图13 横向坐标系与传统坐标系的位置误差曲线图Fig.13 Position error curves of the transverse coordinate system and the traditional coordinate system

由图12和图13可知，使用横向地球坐标系后，双轴惯导系统导航结果稳定正常，无跳变现象发生，且与传统坐标系的导航精度相当，能够验证本文的惯导机械编排方案的正确性。

7 结 论

本文基于双轴旋转调制捷联式惯性导航系统，针对使用传统惯性导航系统机械编排方法在高纬度地区航行时的导航失效问题，分析了使用游移坐标系作为导航坐标系的横向坐标系机械编排方案，通过数字仿真和跑车试验数据进行的半实物仿真进行了验证，说明对于双轴旋转调制惯性导航系统，在高纬度地区使用横向地球坐标系能够解决传统惯性导航机械编排在极区工作时存在的计算溢出、方位陀螺施矩量过大的问题，设备可以维持在较高导航精度下正常工作。