基于模态分析的单轴旋转惯性导航系统结构优化

刘 昱，谢 振，王 伟

（天津航海仪器研究所，天津 300131）

旋转惯性导航系统是旋转调制补偿技术应用于捷联惯导系统而发展形成的。它相较捷联惯导系统多了一个旋转机构，能够在相同惯性元件精度基础上通过旋转调制提高系统导航精度，但结构动刚度会相应地变差，环境动态适应能力降低，不适应惯导系统小型化轻量化的发展趋势[1]。振动问题成为系统性能提升的重要瓶颈。在单轴旋转调制惯性导航系统的结构设计中进行振动模态分析，了解系统结构的振动特性和可能的变形方式，判断结构的性能缺陷和振动风险，并可以围绕其开展优化设计，探寻最佳设计方案，以最大可能地实现系统动态适应能力的优化、满足小型化轻量化设计的需求[2]。

以模态分析为基础进行结构优化，建立准确有效的有限元模型实现可靠模态仿真是关键。单轴旋转调制惯性导航系统连接状态复杂，其模态分析的难点是轴承的等效建模以及妥善地引入转子动力学。在轴承的建模上，研究者一般将其模化为一个无质量的弹性元件。文献[3-5]由线弹性理论出发推导了滚动轴承刚度的理论公式。文献[6]分析了轴承的载荷分布和受载变形情况。关于转子动力学建模方法，文献[7-10]提出了非对称转子系统的支撑结构建模方法，分析了有限元离散格式处理复杂支承转子系统模态计算问题的理论。文献[10]还论述了转子系统的优化设计方法。

本文基于ANSYS有限元分析软件，对单轴旋转调制惯性导航系统进行了合理的有限元建模，通过模态试验验证了等效轴承所采用的无质量弹性元件的参数设置合理有效，最后基于模态仿真对结构薄弱点进行优化，提高了系统的动刚度，使改进后的系统结构达到了一阶模态频率不低于60 Hz的总体设计要求。

1 有限元模型的建立

模态仿真分析的关键在于有限元建模的合理程度。有限元建模可以分为如下5步：

① 建立并简化几何模型；

② 定义材料属性；

③ 确定各零部件之间的连接关系；

④ 划分有限元网格；

⑤ 设置边界约束。

第一步，建立并简化几何模型。系统的大部分结构部件是规则的，进行实体建模并适当简化。温控罩以及电子线路单元对结构力学特性影响不大，在仿真分析中可以直接去除不考虑。

力矩电机、惯性组合件等大质量机电元件和组部件的惯性效应对系统的力学性能的影响是不能完全忽略的。因此，引入了质量点模型进行等效建模。

滚动轴承是轴系的重要支承部件。依据轴承载荷计算公式以及预紧状态下的轴、径向变形公式[3-6]，计算得到本系统轴承的轴向等效刚度径向等效刚度在 ANSYS Workbench平台中选择轴承连接关系模拟轴承支承，并赋予相应的径向刚度和轴向刚度。

简化后的系统结构如图1所示。其以轴承为界划分为支撑结构和旋转部件两部分。支撑结构主要包括底座、支座以及上下两轴承衬套，旋转部件主要包括上下两方位轴、框架以及惯组。

第二步，按照理想加工条件对材料属性定义。

第三步，按照各部件的装配关系设置各个实体或者等效元件之间的连接关系，包括设置轴承连接关系。为了提高仿真效率，利用多体部件功能Form New Part将旋转部件和支撑结构分别设置成多体部件，减少繁杂的接触关系设置。

第四步是网格划分，对轴承、框架以及各连接部位进行网格细化，获得均匀、过度平稳的网格方案。

最后一步是设置接近实际工况的边界约束，合理设置底座完全固定面的大小。

图2 添加控制后的网格方案Fig.2 Mesh scheme

2 系统整体模态仿真

系统的模态特性是各组部件耦合作用的结果，因而模态仿真需要合理反映轴承、支撑结构以及旋转部件的力学特性。单轴旋转惯导系统的旋转部件具有特殊的力学行为，其惯性对系统模态有一定影响。选用ANSYS Workbench平台的转子动力学模块进行系统模态求解。系统前四阶模态频率如表1所示，前四阶模态振型如图3所示。

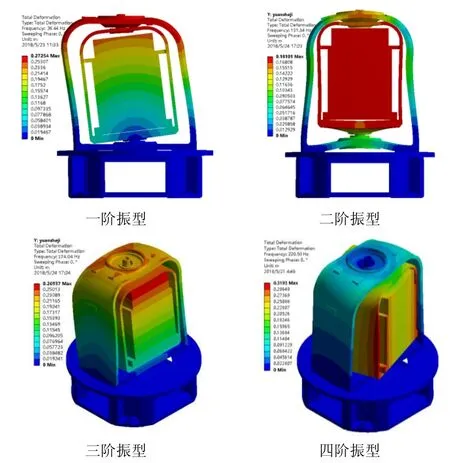
图3 系统整机的前四阶模态振型仿真结果Fig.3 Simulation results of modal shapes

表1 系统整机的前四阶模态频率仿真结果Tab.1 Simulation result of modal frequency

3 模态试验

利用振动台对单轴旋转调制惯性导航系统整机进行模态试验。通过压板将系统固连在振动台刚性台面上。为了有效地识别系统一阶模态，根据模态仿真获得的一阶振型变形形式，将加速度传感器布置在响应明显的支座上部。通过振动测试系统对系统结构施加如下垂向面运动激励：1～16 Hz，位移1.0 mm；16～60 Hz，加速度1.0g。

测得的加速度传感器响应曲线如图4所示，系统的一阶固有频率为34.38 Hz。试验得出的一阶模态频率与仿真结果十分靠近，偏差小于3 Hz，符合度优于90%，说明该仿真模型和方法合理有效。

图4 系统模态试验响应曲线Fig.4 Response curves of modal experiment

4 结构优化

模态试验验证了模态仿真的可信度。基于仿真，可以获得可靠的模态特性，并对设计进行指导并优化。本系统的一阶频率只有34 Hz左右，结构动刚度较差，未达到总体关于系统基频不低于60 Hz的要求，在船载环境下有共振风险。分别对旋转部件和支撑结构进行了模态仿真，了解其固有刚度特性，对两者的耦合关系进行分析。探讨导致系统动刚度差的原因，并采取有效措施提高系统动刚度。

4.1 结构缺陷识别

对旋转部件进行部件级模态仿真，将支撑结构看作刚性基座，轴承用弹性元件等效。前四阶弹性模态频率如表2所示，前二阶弹性模态振型如图5所示。从仿真结果可知，旋转部件薄弱部位在薄壁框架，而自身的刚度较强。

图5 旋转部件前二阶模态振型仿真结果Fig.5 Simulation result of modal shape

表2 旋转部件前四阶模态频率仿真结果Tab.2 Simulation result of modal frequency

对支撑结构进行部件级模态仿真，探究其动刚度特性。支撑结构前四阶模态频率如表3所示，前二阶模态振型如图6所示。从仿真结果可知，本系统的龙门式支承的刚度薄弱部位在支座上段自由端，一阶频率不高，一阶振型与系统整机的一阶振型都主要表现为上部左右舷方向摆动。

表3 支撑结构前四阶模态频率仿真结果Tab.3 Simulation result of modal frequency of support structure

图6 支撑结构前二阶模态振型仿真结果Fig.6 Simulation results of modal shapes

上述部件级仿真说明单轴旋转惯导系统的旋转部件自身动刚度不差，其一阶模态特性较低的主要根源在于支撑结构。支撑结构的一阶振型对旋转部件的弯曲振动模态产生了较大耦合影响，降低了旋转部件的支承刚度，从而大大地降低了整机的一阶模态，恶化了系统的动力特性。因此，系统结构的薄弱点在支撑结构，优化的方向是提高支撑结构的动刚度。

4.2 支撑结构优化设计

原设计支撑结构的一阶振型是支座上部左右舷方向的摆动，支座支撑刚度不够。在结构形式不变的前提下，可以通过加筋等措施来提高支撑的刚度，加筋前后的支撑结构形式如图7所示。

图7 支撑结构改进前后的结构图Fig.7 Supporting mechanism before and after optimization

在尽量少的增加支座尺寸和质量的条件下，设计了多种加筋方案。对改进后的各个结构方案分别进行模态仿真，通过对结果的分析和对比最终确定在支座左右各添加四道长筋条的方案最能兼顾轻量化和提高系统基频的需求。优化后的系统前四阶模态频率如表4所示，前四阶模态振型如图8所示。优化后的系统质量增加2 kg，一阶模态频率从36 Hz提高到74 Hz。

依据上述优化结论对支座结构进行了改进设计，并对改进后的系统整机再次进行模态试验，测试设备、测试条件均与第3节相同。测得的加速度传感器响应曲线如图9所示，系统结构在0～60 Hz的扫频条件下无明显振动响应，说明优化后的系统在0～60 Hz的振动环境中有较好的动态适应能力，实现了系统基频不低于60 Hz的设计目标

表4 优化后的系统前四阶模态频率仿真结果Tab.4 Simulation result of modal frequency after optimization

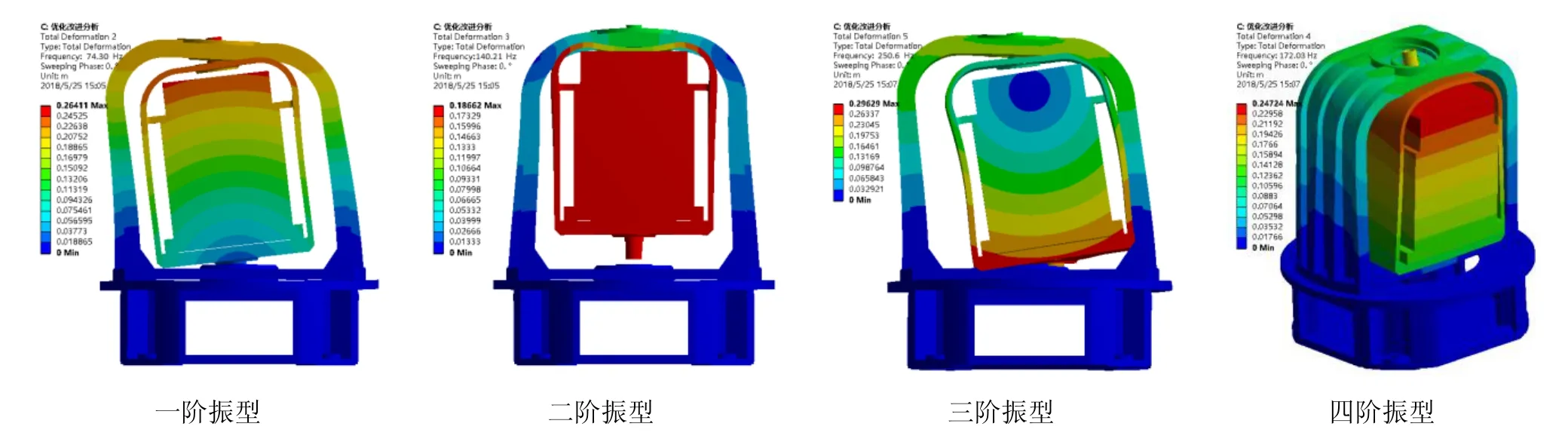
图8 优化后的系统前四阶模态振型仿真结果Fig.8 Simulation results of modal shape after optimization

图9 改进后系统模态试验响应曲线Fig.9 Response curves of modal experiment after optimization

5 结 论

本文通过对单轴旋转惯性导航系统的模态仿真分析，实现了结构动刚度优化，并得到以下结论：

1）单轴旋转惯性导航系统中，龙门式支撑结构的刚度对系统的模态会产生很大的耦合影响，是造成单轴旋转惯性导航系统一阶模态较低的主要原因。

2）单轴旋转系统结构优化的方向是提高支撑结构的动刚度。在结构形式不变的前提下，可以通过加筋等措施提高其支撑的刚度，通过计算机模态仿真的方法快捷地获得合理的结构优化方案。

3）经模态试验验证，单轴旋转惯性导航系统的模态仿真模型和方法合理有效，仿真与试验结果的符合度优于90%。