北斗短基线双天线旋转快速定向方法

2018-08-27蔡体菁许奇梦

中国惯性技术学报 2018年3期

蔡体菁，陈仁，王鑫，许奇梦

（东南大学仪器科学与工程学院，南京 210096）

2018年2月12日北斗三号卫星导航系统的第五和第六颗卫星成功发射，使北斗卫星导航系统向具有国际先进水平的全球定位系统迈进了一大步。利用现在的卫星导航系统不仅可以确定载体的位置，而且还可以确定载体的航向[1-2]。目前越来越多的组合导航系统都用卫星导航系统的导航信息作为它的定位定向的重要信息源[3-4]，因为卫星导航系统具有长时间无漂移、功耗小和成本低的优点[5]。

在我国无人运载器定位定向的应用需求上，北斗卫星导航系统、微惯性测量单元（MIMU）和磁罗盘组合已作为一个首选组合导航系统[6]。但作为一个含有铁质的无人运载器来讲，磁罗盘就容易受到它的磁场干扰，无法正常工作。为了克服这个困难，最近，俄罗斯学者提出一种小体积的GPS罗盘[7-9]。该罗盘主要由GPS双天线接收机、SIMU、旋转机构、控制电路和导航计算机组成。GPS双天线被放置在一个旋转臂上，其基线长度小于0.3m。

使用北斗导航系统给载体定向需要2个天线和1个（或2个）接收机，即北斗双天线接收机。2个天线接收到的卫星信号经同步处理后，获得其卫星星历、原始测量信息（伪距、多普勒频移和载波相位）和导航信息等。通过2个天线接收的载波相位进行差分计算，并利用星历数据，得到双天线基线向量，进而得到载体航向角。在用载波相位处理问题时，必须要事先知道整周模糊度的数值。

目前，求解整周模糊度的方法有很多，可以把它们归为四类[10-12]，分别是基于观测域、位置域、模糊度空间和测量域的整周模糊度求解方法。前三种方法是常用的方法，但是其算法复杂，运算量大。第四种方法算法简单，计算量小，实时性好。

本文针对北斗短基线旋转双天线开展定向研究，提出了北斗双天线基线连续旋转整周和 0°～180°两位置的两种快速定向方法，并通过自行设计研制的转动机构进行了试验验证。

1 短基线快速定向方法

把一对北斗天线安装在一个小尺寸的旋转机构上，使双天线基线绕其对称轴快速旋转，此时北斗双天线接收的载波相位值呈周期性变化，利用北斗卫星载波相位双差值，连续积分一个周期，或取 0°～180°两位置上的值，得到浮点模糊度双差值，进而获得双天线基线航向角，通过旋转机构角度输出值，就可得到载体的真实航向。

1.1 北斗载波相位双差模型

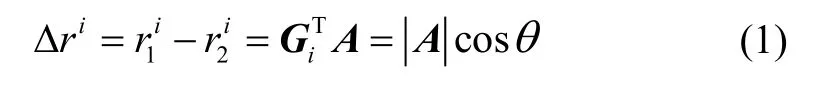
图1 天线与卫星几何关系图Fig.1 Geometry diagram of antennas and satellite

北斗天线载波相位观测方程为

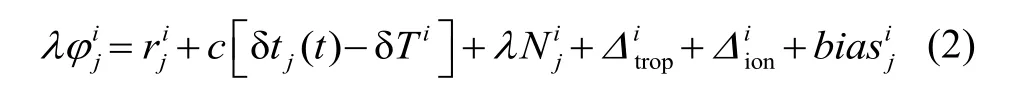
对于短基线北斗双天线而言，可以认为两个天线接收的信号受对流层和电离层的影响相同，那么两个天线对北斗卫星的载波相位测量值之差为

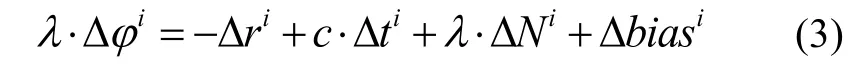
将式(1)带入式(3)得：

从式(4)可知，载波相位单差分只能消除北斗卫星的钟差，无法消除北斗接收机的钟差。为了能够消除接收机之间的误差，考虑在两天线载波相位测量值之差的基础上，对不同的北斗卫星之间再做一次差分。

假设北斗天线R1、R2同时接收到的北斗卫星的数量在4颗及4颗以上，选取其中的卫星作为参考卫星利用式(4)得到北斗双天线载波相位双差数学模型：

1.2 单位向量计算计算

北斗卫星导航系统的空间卫星由5颗地球静止轨道（GEO）卫星、27颗中地球轨道（MEO）卫星和3颗倾斜地球同步轨道（IGSO）卫星组成。卫星编号1～5为GEO卫星，卫星编号6～35为MEO/IGSO卫星。

对于1～5号北斗静地轨道卫星，在CGCS2000地心坐标系下位置坐标的计算公式为：

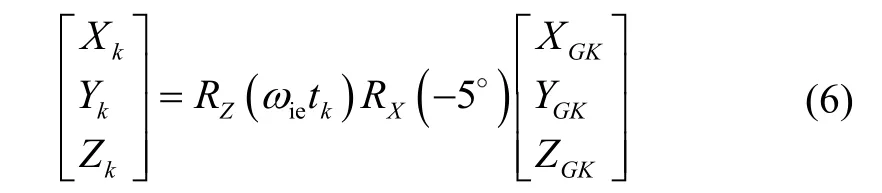
对于6～35号MEO/IGSO卫星，在CGCS2000地心坐标系下位置坐标的计算公式为

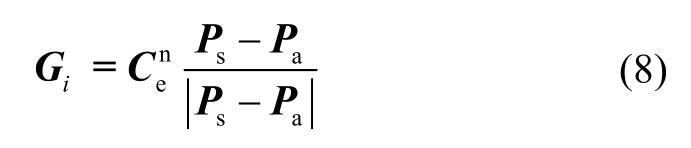
1.3 整周模糊度计算

利用载波相位确定天线的位置，通常需要求解整周模糊度。目前有基于观测域、位置域、模糊度空间和测量域的整周模糊度求解方法。前三种解算方法很复杂，运算量很大。第四种算法简单，计算量小，实时性好。本文提出利用北斗双天线基线连续旋转整周和0～180°两位置来确定整周模糊度双差值。

式(9)代入式(5)，有：

在短时间内北斗卫星到天线的单位向量不会发生显著变化，可以认为基线向量旋转前后单位向量没有变化。北斗卫星载波相位双差值随基线转动角度变化曲线如图2所示。

图2 连续旋转时载波相位双差值曲线Fig.2 Carrier phase double-difference curve during continuous rotation

将北斗双天线基线连续旋转一周，对式(10)进行积分，可得载波相位双差浮点模糊度：

对于离散数据，近似式为：

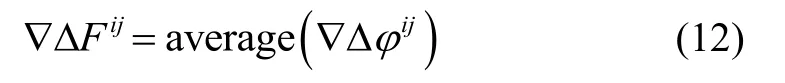
此外还可以将北斗双天线基线旋转 180°，通过0～180°两位置的载波相位双差值，利用式(10)，将旋转前后0～180°两位置的载波相位的双差值相加，得到载波相位双差的浮点模糊度：

1.4 航向角计算

当天空中有4颗或4颗以上的卫星时，假设北斗卫星的基准星标号为1，其它标号为2,3,4…。那么方程(5)可改写为

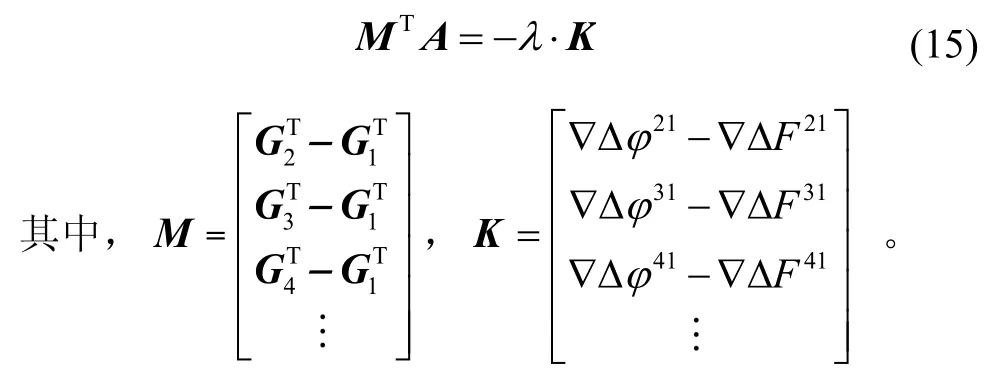
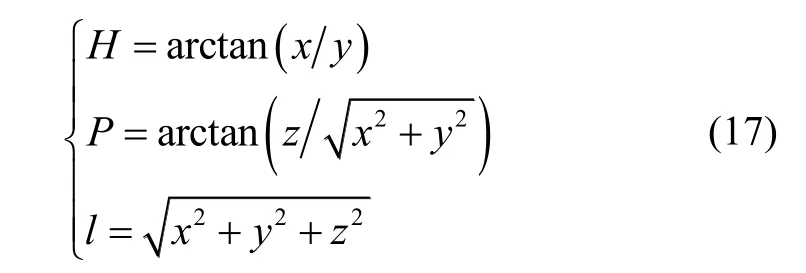
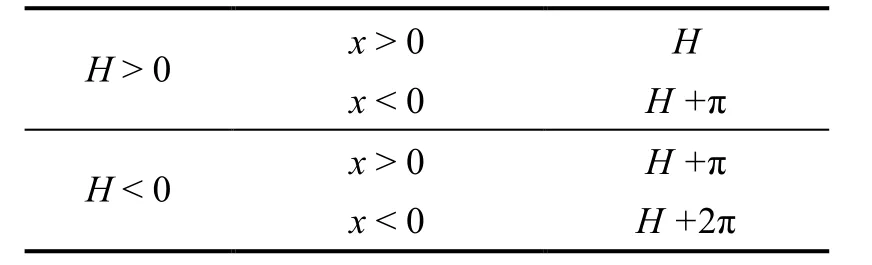
表1 航向的象限转换方法Tab.1 Quadrant conversion method for the heading

2 实验结果

北斗双天线定向方法试验验证装置主要由 2个北斗天线、1块北斗OEM板卡、转动机构、中央控制解算单元和电源模块组成，如图3所示。两天线固定在电机转子上，两天线的中心距离为30 cm。

在电机基座静置的情况下，系统上电，等到北斗双天线都能接收到6颗卫星信号时，电机带动天线以某一速度旋转一周，停留一定时间，再让电机以某一速度正转180°，停留几秒，然后反转180°停止。

图3 实验装置Fig.3 Experimental device

利用上文给出的两种求载波相位双差浮点模糊度的方法，计算载波相位双差浮点模糊度，结果见表2。从表2可以看出，两种方法得到载波相位双差的整周模糊度都相等。

表2 载波相位双差浮点模糊度Tab.2 Floating ambiguity of carrier phase double-difference

为了验证上述方法计算航向的准确和快速性，进行如下试验：在电机基座静置的情况下，系统上电，等到北斗双天线都能接收到4颗以上卫星时，电机带动天线以某一速度旋转一周后静止。在这个试验中，采用了某公司的617D OEM板卡作为对比板卡，该板卡具有双天线基线航向角输出功能，便于结果比较。在同一情况下进行了多次试验，航向角和基线长度计算结果见表3。

以第3次试验数据，本文方法计算的航向误差与对比板卡输出航向误差对比以及基线长度误差见图4。

本实验基座的航向参考值为40.06°，它是由激光陀螺定位定向系统获得的。由表3可以看出本实验方法获得的航向精度优于1°。上述定向方法只需要主次天线同时接收到4颗卫星就可以快速正确的确定载体航向。而对比板卡只有在6颗星时才能够输出较好的航向角，输出精度还没有本文的定向方法好。

表3 实验结果分析Tab.3 Analysis of the results in the experiment

图4 实验解算的航向误差与北斗板卡输出航向误差对比和实验计算基线长度误差曲线Fig.4 (a) Comparison between experimental heading error and the heading error by Beidou receiver; (b) baseline length error obtained by experience

经过多次试验，在保证两北斗天线同时接收到 4颗或4颗以上卫星时，用本文连续旋转定向方法只需要20 s便能确定基线航向。若是在北斗卫星信良好的位置冷启动，3 min内就可以确定基线航向。

为了验证试验的动态特性，又进行如下实验：在电机基座静置的情况下，电机先上电归零，然后系统上电，等到两北斗天线同时接收到6颗卫星时，让电机带动天线以某一速度连续旋转。

将实验计算的基线航向减去同一时刻的电机角度值得到电机的初始零位航向。电机静基座旋转的情况下该航向保持不变。用实验数据计算的航向与对比板卡输出值对比曲线如图5所示。激光陀螺定位定向系统给出的电机零位航向为93.27°。从图5中可以看出，在基线旋转的过程中本文方法计算的基线航向角精度比对比板卡输出的要好。