联合多普勒的载波相位精密测速方法

姚 曜，张 帆，杜红松，王 涵

（1. 中国人民解放军91977部队，北京 100036；2. 中国人民解放军92981部队，北京 100161）

目前主流的速度测量方法有惯性导航测速以及基于GNSS系统的速度测量等[1]。惯性系统具有自主性，但其测速存在误差积累的问题。GNSS测速精度高，是一种理想的速度测速方法[2]。当前GNSS测速方法主要包含位置微分测速、多普勒观测量测速和载波相位差分等三种，这三种方法特点有：1）位置微分测速法是通过位置微分获得速度的方法，优点是测速方法简单，但此方法受单点定位精度影响明显，测速精度一般只有0.2 m/s，实际无法应用在高精度测速的场合；2）多普勒测速基于卫星和用户间的多普勒效应测速，优点是可靠性高，而且理想的条件下测速精度可以达到2 cm/s[3]，文献[4]对多普勒测速方法进行分析测试，其中在静态条件下多普勒测速可以达到1～2 cm/s的精度；3）载波相位测速方法优点是测速精度高，目前可实现mm/s级别的测速精度[5]，然而该方法无法避免整周模糊度跳变的影响。通过以上分析，为了实现高精度测速精度，需要引入载波相位观测量，但传统的载波相位时间差分方法没有考虑观测噪声以及周跳的影响，其中噪声是影响测速精度的主要误差源，而周跳是影响该方法测速可靠性的主要风险源之一，为了消除周跳以及降低观测噪声对载波相位测速法的可靠性影响，本文提出多普勒联合载波相位的两步精密测速方法，该方法首先通过多普勒检测并排除周跳的影响，由此利用无周跳影响的载波相位时间差分作为观测量，通过 Kalman滤波降低高频噪声的影响，使得该测速方法在满足高精度的同时免受周跳的影响。

1 载波相位差分测速算法

载波相位是GNSS中基础的观测量，相比伪距观测量具有更高的精度，因此被广泛应用在高精度领域。根据载波相位观测量的特点，可以通过相邻历元时间差分的方式获得载波相位时间差分观测量进行高精度速度测量。

1.1 载波相位差分测速模型

载波相位定位的原始观测方程，

式中，l表示载波波长，j为以周为单位的载波相位观测值，r是卫星与接收机之间的几何距离，δtu是接收机时钟误差，是卫星时钟误差，I是电离层延时，T是对流层延时，N为整周模糊度，e为其余误差[6]。

将卫星与接收机的几何距离变化△r用卫星位置和接收机位置x以及观测矢量表示，将两个相邻时刻位置变化线性化[8]，其中，v表示 tk-1到tk时间段的平均速度，得到测速解算方程为

式中，△g是与卫星和接收机位置及观测方向矢量有关的量[9]，

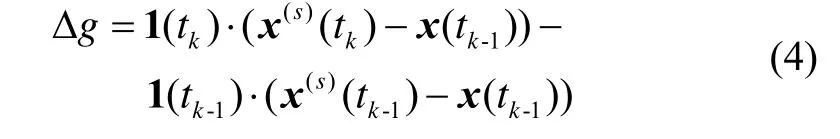
可以通过最小二乘法或Kalman滤波求解平均速度v。

Kalman滤波是一种递推线性无偏最小方差估计方法，通过系统的状态转移方程，根据前一时刻的状态估值和当前时刻的观测值递推估计新的状态估计值，进而可以降低高频噪声的干扰。与最小二乘法相比，Kalman滤波更适合于动态定位数据处理[10]，因此本文采用Kalman滤波解算。

在 tk时刻将随机线性连续系统离散化，状态方程：量测方程其中，时刻系统状态向量，øk|k-1为状态转移矩阵；为观测量与状态量之间的量测矩阵；wk为过程噪声向量，vk为测量噪声向量，采用大地坐标系WGS-84表示解算的速度值，作为状态量。

以动态测量为例，来说明 Kalman模型设计，其中，量测值残差zk表示为

式中，n为观测卫星数，设置状态转移矩阵øk|k-1和量测矩阵Hk，

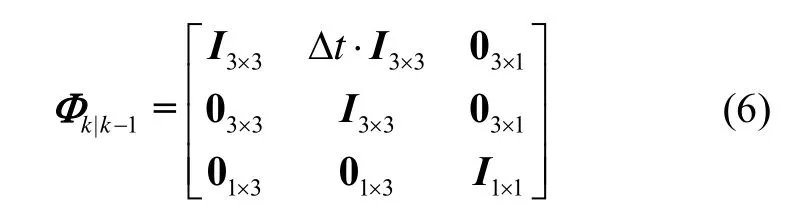
式中，I表示单位阵,Dt为采样间隔。

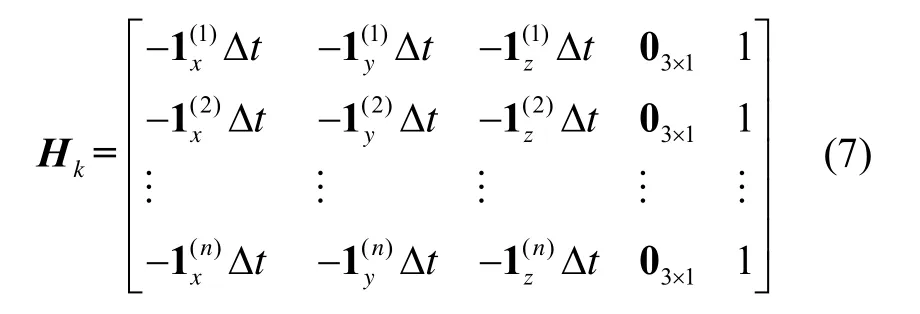
采用卫星高度角加权模型设置测量噪声vk协方差阵R，即：

式中，系数a为载波相位噪声系数，根据经验值，选择系数=3mma，qi为第i卫星高度角[11]，则量测噪声只是卫星高度角的函数，由于时间差分将会放大噪声方差为原来的2倍，因此系数需要乘2。根据经验，选择每颗卫星过程噪声都服从相互独立且均值为 0，方差为0.005的正态分布，即

设后验均方误差阵Pk初始值为主对角线100的7阶方阵，并通过Kalman滤波预测过程进行迭代更新。通过 Kalman滤波的预测和校正递推过程，可以解得速度状态量

1.2 联合多普勒周跳检测方法

当接收机在对载波相位观测量进行连续观察时，若追踪环路无法保持锁定载波信号，则可能会丢失掉个整周，导致两个时刻间的载波相位变化量的测得值相差了个整周期[12]。当发生周跳时，时间差分的观测方程改写为

针对周跳现象对载波相位时间差分测速法的可靠性带来严重的影响，本文提出一种联合多普勒的载波相位精密测速方法。

设卫星s在轨道上以速度v(s)运行，用户接收机以速度v运行时，由于多普勒效应，产生多普勒频移fd=通过与载波相位时间微分方程联立，可以得到多普勒频移观测量的解算方程，

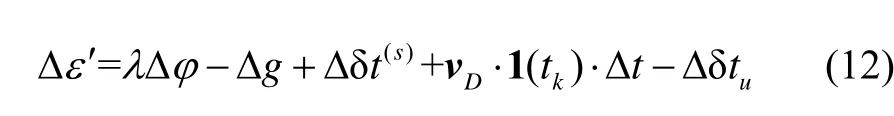
式中，vD为通过多普勒方法解算的速度，为联合多普勒的载波相位测速方法的速度残差量，可以用来判断是否发生周跳，本文采用c2假设检验方法。

假设n个方程残差量服从相互独立且均值为0，方差为s2的正态分布，SSE（Sum of Square for Error）代表速度测量残差平方和，即则对应的统计检测量服从自由度为3n-的c2分布。在同一历元内观测方程个数为n时，取c2检验，

式中，Pa为拒绝检验概率，可以得到门限值T，当观测方程不满足上式，即拒绝假设，则该历元出现周跳现象。

在检测到历元发生周跳，为了可以通过载波相位差分的方式实现高精度测速，需要剔除周跳卫星观测量，仍然可以通过其它非周跳卫星观测量保证该方法测速的高精度性，采用3s准则对周跳历元进行进一步检测的方式。依次检验出现周跳历元的n个残差值，通过多历元标准差平均得到标准差s，设该历元第i个残差为再由3s准则，当检测到即认为该卫星观测方程发生周跳，需要将该受到周跳影响的观测量剔除。

在同一历元的n个有效卫星中，当没有周跳影响的n'个卫星数满足可以通过本文方法精确计算接收机运行速度；当 4n¢时，即卫星过少或相出现过多周跳卫星，若此时总有效卫星数n≥4，通过多普勒方法计算的速度作为该历元速度；当总有效卫星数 4n时，根据卫星导航定位及测速原理，无法直接计算该历元速度。

2 实验测试

本文分别设计了静态与动态两组测试实验，通过与传统测速方法进行对比，从测速精度及可靠性两方面综合评估所提出联合测速法的测速性能。实验通过Novatel-ProPark6接收机以1Hz采样率获得GPS观测数据，静态测试采集时长1.5 h，动态测试采集时长2 h。为了测试周跳现象对实验测试的影响，人为注入周跳以判断该方法检测周跳的能力。采用静态试验中每10 min在1颗卫星观测量加2周的周跳，动态实验中每10 min在1颗卫星观测量加5周周跳的方式。为有效评估测速算法的性能，本实验采用平面距离均方根（Distance Root Mean Squared, DRMS）、天向轴向均方根（Up Root Mean Squared, Up RMS）及球概率误差SEP95（Sphere Error Probability of 95%）等三种统计量综合评估算法测试速度精度及可靠性性能。

需要说明的是，由于动态测试没有准确的测速参考，考虑到动态测试环境为水平路面，取其天向方向上的运动作为误差比较方向。而实验场地并不是理想水平，导致试验车处于摆动、颠簸的状态，使得天向速度真值不能绝对为零。

2.1 静态测试

图1展示了传统位置微分测速法、多普勒测速法、载波相位测速法静态测试在东向、北向和天向速度结果。

图2展示了载波相位测速法无周跳检测方法与多普勒检测周跳方法在东向、北向和天向速度对比结果。

图1 传统测速方法比较Fig.1 Comparison of traditional velocity measurement methods

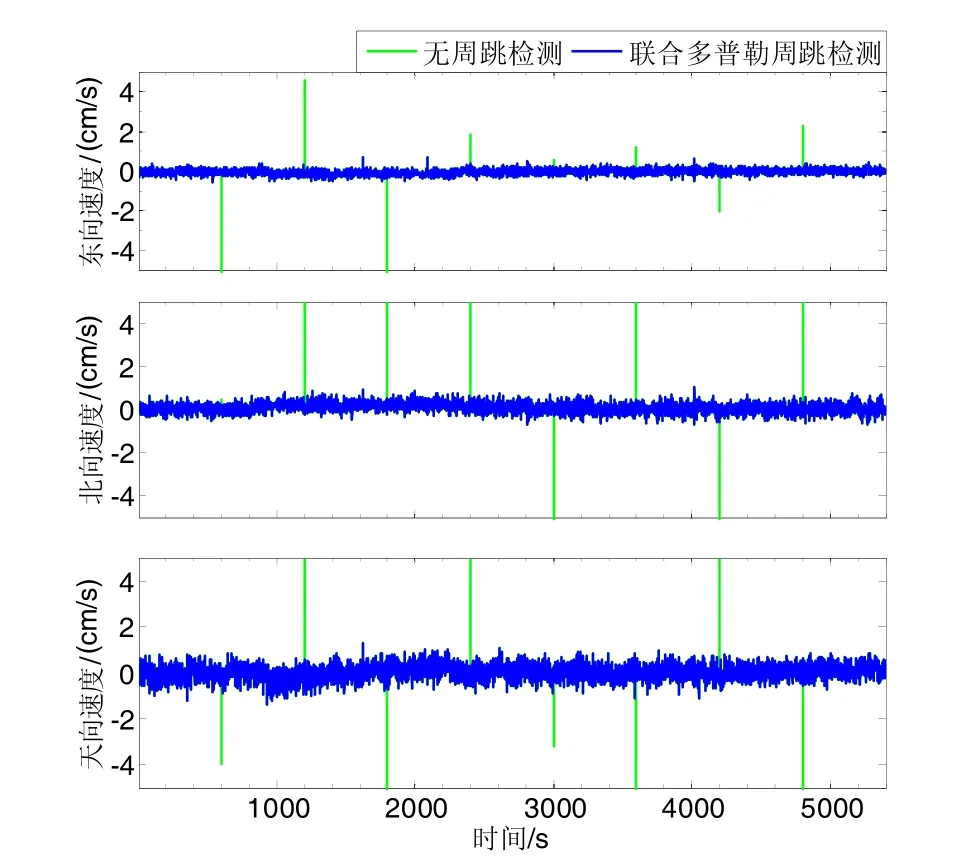
图2 载波相位周跳检测对比Fig.2 Comparison of carrier phase cycle-slips detection

表1展示了载波相位时间差分联合多普勒法和传统的位置微分法、多普勒法以及载波相位差分法测速精度对比结果。

表1 载波相位时间差分联合多普勒法与传统测速方法静态测试精度比较Tab.1 Comparison on static test precisions among the four methods

从表1可以看出，位置微分法测速误差SEP95为3.7 cm/s，速度误差比多普勒测速法的测速误差7.1 cm/s降低48%，其原因是位置微分法受接收机性能影响较大，而ProPark6接收机对于伪距观测量采用了相位平滑算法，有效提升单点定位精度。相比于位置微分测速、多普勒测速，相位差分法的测速精度达到7.4 mm/s，可实现mm/s级的测速精度需求。但是从图1中发现，由于传统的相位差分测速法并未考虑周跳的影响，导致存在多处测速异常点，有周跳影响下的 DRMS为6.1 mm/s。由此可见，周跳现象是相位差分测速法影响可靠性的主要干扰源。本文提出的一种联合多普勒的载波相位精密测速方法，可以对周跳点进行检测并剔除。通过周跳检测，剔除周跳卫星，成功消除载波相位测速的全部速度异常点，含周跳检测的测速误差DRMS由6.1 mm/s降到2.8 mm/s，在满足载波相位时间差分测速的精度下，实现测速的可靠性。

为了进一步提升静态测速性能，采用 Kalman滤波算法对观测量的高频噪声进行优化抑制，设置测量噪声协方差阵R，其中参数a=3 mm。图3展示了载波相位包含周跳检测，并分别通过最小二乘法与Kalman滤波解算结果对比。

图3 载波相位周跳检测对比Fig.3 Comparison of carrier phase cycle-slips detection

表2展示了最小二乘法、Kalman滤波精度比较结果。由表2比较可知，在静态试验中，Kalman滤波解算速度误差SEP95由最小二乘法的7.40 mm/s下降到1.10mm/s，体现了 Kalman滤波在对高频噪声的抑制作用。

表2 最小二乘法和Kalman滤波静态测试比较Tab.2 Compa rison on static test precisions between least square method and Kalman filter method

通过以上静态实验结果比较可知：通过联合多普勒的载波相位时间差分测速方法可以达到 mm/s级的精度，并且通过周跳检测，消除了周跳带来的野值影响；同时，采用 Kalman滤波方法测速精度得到了进一步的提高。

2.2 动态测试

车载动态测试时间是2016年5月10日12:30～14:30，采用Novatel-ProPark6接收机以1 Hz频率采样，共绕哈尔滨工程大学军工操场15圈，运行轨迹如图4所示。

图4 车载动态实验运行路线Fig.4 Vehicle running route in dynamic experiment

图5展示了动态位置微分法、多普勒法和载波相位差分法在东向、北向和天向的测速结果，图6展示了联合多普勒的检测周跳法和无周跳检测的速度结果。

图5 传统测速方法比较Fig.5 Comparison of traditional speed measurement methods

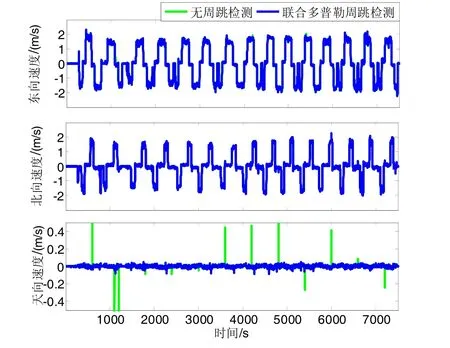
图6 载波相位周跳检测前后对比Fig.6 Comparison on with and without carrier phase cycle-slips detection

从图5可知，位置微分测速方法在天向上出现多处达到 1 m/s的野值点，因此实际难以应用在高精度场合。相比位置微分法，多普勒测速可靠性表现更明显，其中在天向上测速误差RMS为6.3 cm/s，天向95%点为 12 cm/s。通过传统的载波相位测速方法，天向95%点速度误差由多普勒测速方法的 12 cm/s下降到2.4 cm/s，然而由于多处点受到周跳影响，天向速度误差RMS由多普勒测速法的6.3 cm/s扩大到29 cm/s，可见周跳现象对载波相位测速可靠性产生很大影响。通过图6周跳检验前后对比，联合多普勒的载波相位方法，消除了所有的周跳野值点，天向速度误差RMS由无周跳检测的29 cm/s降到1.3 cm/s。

为了进一步提升动态测速性能，采用 Kalman滤波算法对观测量的高频噪声进行优化抑制。图7展示了联合多普勒的载波相位测速方法由 Kalman滤波法与最小二乘方法解算速度比较。

图7 Kalman滤波法与最小二乘法比较Fig.7 Comparison between Kalman filter and least square methods

从图7比较可知，联合多普勒的载波相位测速方法，通过Kalman滤波解算，天向速度误差95%点由最小二乘的 2.4 cm/s下降到 2.1 cm/s，天向速度误差RMS由最小二乘的1.3 cm/s降到1.1 cm/s。从天向方向上看，Kalman滤波比最小二乘法收敛更加明显。

图8展示了联合多普勒的载波相位测速方法与传统多普勒法测速方法之间的比较。与联合多普勒的载波相位测速方法相比，多普勒测速噪声较为明显，载波相位测速天向误差95%点由多普勒测速法的12 cm/s下降到2.1 cm/s，相比多普勒方法体现该方法测速精度的优越性。

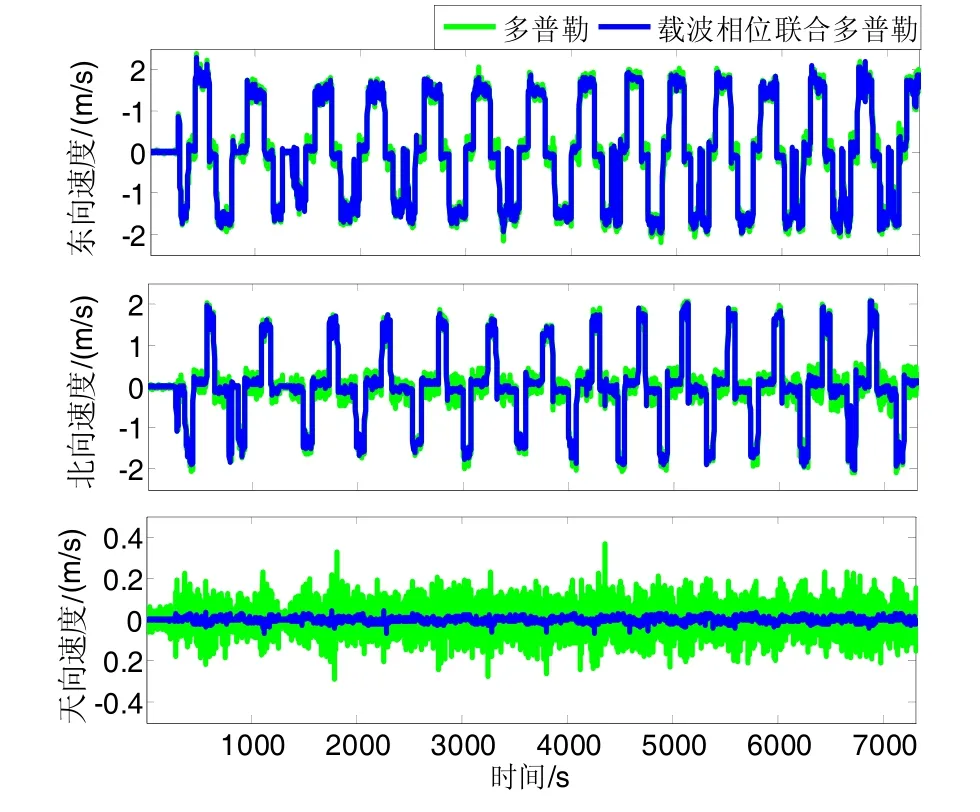
图8 联合多普勒的载波相位法与多普勒法比较Fig.8 Comparison between “Doppler + carrier phase”method and Doppler method

3 结 论

本文提出一种联合多普勒的载波相位精密测速方法，一方面，通过Kalman滤波降低高频噪声的影响，另一方面，通过与多普勒测速法联合，检验并剔除周跳的影响。最后，通过静态和动态试验测试该测速方法的精度。动态测试中，该方法测速误差在天向方向上95%的点相比多普勒测速法的12 cm/s下降到2.1 cm/s，因为动态实验路面不是理想水平，天向速度呈现的周期规律每圈一致，可见实际动态测速应该达到了优于2 cm/s的精度，并且可以检验2周的周跳。试验结果表明，该方法测速精度优于传统的方法，并且消除了周跳的影响，验证了该测速方法具有高精度同时保证了可靠性。