全等三角形的判定专题复习教学

谭静雪

[摘 要]初中阶段图形之间最重要的关系之一就是全等，而全等三角形的判定又是引导学生学会演绎证明的重要内容.在全等三角形的判定专题复习课中引导学生回归知识起点，总结归纳，更好地寻找解题方法，对学生之后的学习有实际意义.

[关键词]全等三角形；判定；复习；初中数学

[中图分类号] G633.6 [文献标识码] A [文章编号] 1674-6058（2018）17-0016-02

初中阶段图形之间最重要的关系之一就是全等，而全等三角形的判定又是引导学生学会演绎证明的重要内容.在全等三角形的判定专题复习课中，引导学生回归知识起点，追本溯源，利用平移、旋转、轴反射来研究三角形全等的判定，快速找到解题突破口，灵活添加辅助线解决问题，总结归纳解题方法，对学生之后的学习有实际意义.

一、教学目标

（1）理解并掌握全等三角形的判定定理；

（2）会应用判定定理进行推理判定两个三角形全等.

二、教学重点、难点

全等三角形的判定定理；灵活应用判定定理解题；会添加辅助线证明三角形全等.

三、教学过程

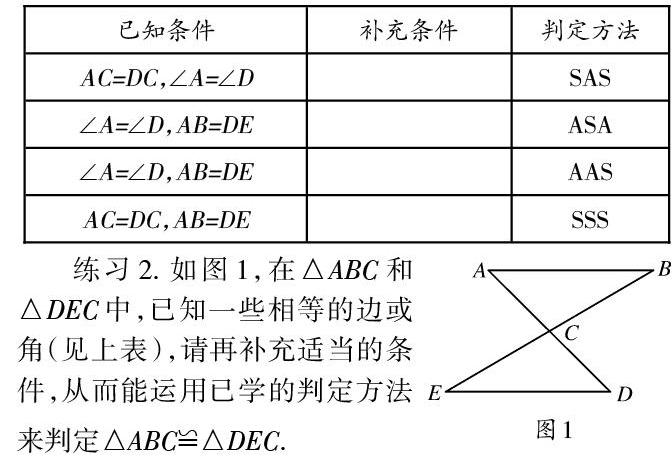
【设计意图】学生推理能力的发展是一个长期的过程，教学中充分考虑了学生的身心特点和认知水平，注重了教学要求的层次性.判定两个三角形全等，直接可用的条件由多到少，由论证一次全等过渡到论证两次全等，图形由简单到复杂，证明的结论由“全等”递进到“边或角等”，从不需要添加辅助线到需要添加辅助线.这样使得推理证明层次分明，坡度平缓，更有助于学生学习综合法证明.

【设计意图】添加辅助线解题是本题的关键，如何引导学生添加辅助线则是教学的重难点.方法一利用旋转的观点作出辅助线DG，得到△DGF≌△ECF，从而得到DG=CE，再证明DG=AD，从而得到DG=AD=CE.方法二利用旋转的观点延长FC到N，使得FN=FA，得到△ADF≌△NEF，则NE=AD，再证明CE=NE，从而得到NE=CE=AD.通过两种方法拓寬学生思路，发散学生思维，加深学生对利用旋转的观点构造全等三角形，打开思路突破重点、难点，从而解决问题的优越性.

综上所述，在作辅助线的过程中，改变以往强调从三个判定条件入手找辅助线的抽象做法，引导学生回归知识的起点，利用平移、旋转、轴反射等方法变换得到全等三角形，让学生在学习中弄懂知识的来龙去脉，找到作辅助线的诀窍，培养学生学习的兴趣和逻辑推理能力.

（责任编辑 黄桂坚）