刍议初中数学“问题解决”

沈春梅

[摘  要] 在核心素养培育的背景下，对问题解决的理解需要紧扣“问题”“问题解决”等几个核心概念来进行. 其中，问题不是生硬的，是“认知困难”与“情感”相互作用的产物，问题解决需要重点突出试错意味.

[关键词] 初中数学;问题解决;教学论视角

初中数学教学中，问题解决被视为具有高度综合性的过程，学生在问题解决中需要利用已有的知识或经验，对面临的问题进行抽象、建模，以实现问题的解决. 在核心素养被提出之后，研究者对问题解决进行了进一步理解与拓展，并将之放到了教学论的视角下进行研究，这样的研究过程与结果给了一线教师很大的启发，在此笔者试结合自己的教学经验，谈谈教学论视角下对问题解决的进一步理解.

初中数学教学视角下的“问题”

问题在数学教学中无处不在，在学生的生活中也无处不在，当在教学的视角下观照这些“问题”的时候，可以发现问题有着超越经验的意义. 今天的数学教学强调生活与数学的联系，而问题在这个联系过程中也起着非常重要的作用. 于是就可以得出一个重要的结论，那就是学生在数学学习中，问题可以从生活中来. 当然，这里的问题是指数学问题，于是从生活中抽象出数学问题，就是数学教师的一个重要任务（这里所涉及的数学抽象，实际上就是数学学科核心素养的重要组成部分之一）. 问题除了从生活中来之外，自然也可以从逻辑推理中来. 很多时候我们在课堂上通过对前面知识的复习提出新的问题，实际上就是沿袭的这一教学思路.

从教学论的视角来看，我们仍然认为问题不能是学生直觉性的反应，而应当是“认知困难”与“情感”相互作用的产物.

我们可以通过“多边形的内角和”的例子来理解这一阐述：学生在学习多边形的时候，一个重要的知识基础就是对三角形的认识. 学生理解多边形本身并没有困难，但在寻找多边形内角和公式的时候会出现困难，这个困难主要体现在学生可以推出四边形、五边形的内角和，但对于普遍规律却难以把握——这就是认知困难. 在产生这个认知困难之后，由于问题解决动机的驱动，学生的情感自然会处于一种疑惑、焦躁甚至是急躁的状态，这种状态对于问题解决来说并非完全是坏事，因为其极有可能转化为学生解决问题的动力.

进一步研究表明，问题反映的是学习者“理想与现实的差距”，当一个问题出现在学生面前时，“理想”就是问题的答案，而“现实”就是问题的题设，题设与答案之间的距离，反映着理想与现实之间的差距. 从教学论的视角来看，当这个差距的缩短在学生的能力范圍之内时，学生解决问题的动机是最为强烈的，而这一认识与“最近发展区”理论又是异曲同工的，所以说教师在分析并帮学生厘清问题的时候，一个最基本的原则，就是要在把握学生认知的基础上，判断学生的现实与理想之间有多大的距离.

譬如上例中，学生的认知“现实”是对三角形内角和的认识，是知道多边形可以“拆”成三角形，而“理想”则是如何寻找到一个一般性公式来描述多边形的内角和. 其中的距离在于学生通过逐步列举四边形、五边形等图形的基础上，猜想多边形内角和表达式的共性，然后表述为（n-2）×180°. 这个猜想与论证的过程，对于大多数学生来说都不是太大的困难，因而这个理想与现实之间距离缩短的过程，就是学生可接受的，进而问题解决的过程通常就是成功的.

这里特别需要指出的是，数学学习的过程中，当学生能够用数学语言来描述问题时，实际上已经经历了一个从自身的经验走向理性的过程，因此有人界定问题为“从经验走向理性的桥梁”，笔者以为这样的界定，也能够给数学教学带来很多有益的启示——譬如这个桥梁如何搭成，又如何才能牢固等.

教学论视角下理解“问题解决”

目前对问题解决的普遍认识是，问题解决不是一个运用固定理论方法或固定程序，去实现从题设到结论的方法. 也就是说尝试建立一套固定的、普适的问题解决的模式，是不可行的. 更多的时候，问题解决带有“现象学”的意味. 在问题解决的过程中，由于学习者思维方式、经验基础的不同，具体的解决问题的心理过程是有着一些差异的. 但是，这并不意味着问题解决真的毫无规律可循，否则也就没有教育、心理方面的专家对这一领域实施研究了.

研究表明，从教学的角度看问题解决，其具有试错的特性. 应试形态下的初中数学教学，总追求学生在解题的时候思路正确且迅捷，这从应试的角度来说是必需的，而从学生思维发展尤其是核心素养培育的角度来看，则是不合适的. 因为学生在真正的问题（非完全指数学领域）解决过程中，总会经历对问题的分析、判断等过程，此过程中总有失误的时候，关于这一点，问题解决研究者提出了“可错性学说”，该学说认为“错误是件好事情”. 而在学生的学习过程中，错误其实也是难以避免的，作为数学知识、数学思想方法与数学思维综合性很高的问题解决，避免出错也是不可能的事情. 因此，在问题解决教学中吸纳“可错性学说”，将试错当成问题解决的重要思路，也是可取的.

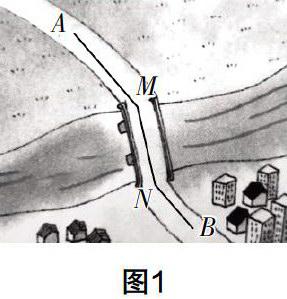
最具说服力的例子来源于教材上的一些“课题学习”，如人教版教材中的“最短路径问题”，这是利用轴对称知识来解决的一个问题，在对其中的“造桥选址问题”（如图1）的分析中，笔者发现好多学生难以利用轴对称知识建立直接的模型. 在建立模型的过程中，学生试图通过轴对称来寻找到最短的路径，结果在画图的时候因为有“桥必须与河垂直”的要求，导致在草稿纸上画出的图形错误、修正、再错……

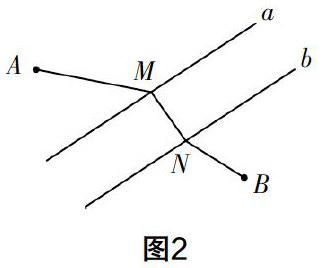
这种试错在笔者看来是有益的，因为学生在试错的过程中，必须完成数学抽象的过程，即将实物图转换为几何图形（如图2），这实际上是在不断地尝试轴对称知识在其中可以发挥什么样的作用，同时也是对图中AM+MN+NB最小值的不断摸索. 当学生发现此问题解决的过程中不仅需要轴对称，还需要平移，进而最终将问题转换为：N点在直线b的什么位置时，所求距离是最小的？

这样的试错，实际上将学生的思维整个进行了一次梳理，学生所猜想的所有情形都出现了一遍，学生不仅知道了正确方法对在何处，也知道了错误方法错在哪里. 这样，学生思维中就既有对的认识，又有错的认识，这样学生的思维是全面完整的，问题解决的思路是全面清晰的. 教师在教学的过程中，只要重点强调一下正确思路，让学生形成解题思路即可. 这样的试错过程，不仅不会影响学生的应试能力，还会因为其经历了完整的、由错到对的探究过程，从而保证学生的数学学科核心素养可以得到有益提升.

当然，问题解决的重心不只在试错上，在问题解决的过程中，培养学生的创新思维、批判思维，让学生在问题解决之后总结自己的思维过程，提取其中有益的那部分，让学生从自己知识结构与方法完善的角度去思考问题解决的过程有哪些收获，都是可以提升学生的问题解决能力的，都是可以培养学生的数学学习品质的. 这些方面其实都是问题解决研究的主题内容，而笔者在此重点强调试错，是因为看到在传统研究中这个话题有些薄弱，故重点强调.

“问题解决”之于教学的意义

问题解决能力无疑是学生应当具备的关键能力，这就是说在核心素养指引教育教学改革的背景下，问题解决将成为通过数学教学提升学生核心素养的重要途径.

但这样的表述仍然显得过于笼统，从教学论的视角来看问题解决的意义，应当建构这样的几点认识：其一，问题解决可以让教师更好地反思初中数学教学. 数学教学不是纯粹地教数学知识，还要教会学生数学思想方法，让学生学会用这些方法，而这个目标，只有在问题解决的具体过程中才能实现. 著名哲学家亚里士多德说过，“对于要学习才会做的事情，都是通过那些学会后应当做的事情来学习的”，这与中国常说的“在游泳过程中学会游泳”是一个道理，只有在问题解决的过程中才能培养问题解决能力，从而让数学教师更好地认识到数学教学的价值. 其二，问题解决可以促进教师重构数学学科教学体系. 问题解决引导下的数学教学，可以让教师形成问题解决导向的教学思路，从而让学生的数学学习围绕问题解决来进行，这样可以让学生的数学学习具有一个完整的问题解决情境，从而促成学生的问题解决过程.

总之，在教学论视角下，初中数学本着问题解决的思路去教学，可以促进教师更好地建立数学教学的思路，促进学生数学知识体系的建构，最终促进核心素养的养成.