论锐角三角函数概念教学

周小云

[摘  要] 在实际教学中，很多老师教学锐角三角函数的概念过于简单，丝毫未触及函数的本质，更未体现锐角三角函数的函数特性. 基于此，本文对初中锐角三角函数概念教学方法做了详细阐述，希望对同行有一定的参考、借鉴作用.

[关键词] 锐角三角函数;概念;教学

对于初中锐角三角函数的概念，最常见的教学方法是：根据课本讲解锐角三角函数的定义. 比如教学正弦函数时，先下定义：在直角三角形中，锐角∠A的对边比斜边，叫∠A的正弦函数，记作sinA=■，然后通过练习加以巩固. 殊不知，这种教法只能让学生记住定义，其完全背离了数学教育的初衷——发展学生的逻辑思维，培养学生的数学思维品质. 这样处理教材的方式肤浅、死板，根本不能让学生体会到锐角三角函数的函数特性. 笔者经过多年的实践摸索，发现了一套锐角三角函数概念的教学方式，其不仅成功避免了寻常肤浅、死板的教学方式，还很有效果，现介绍如下.

奠定一个基础

先奠定一个基础——在直角三角形中，当锐角一定时，不论三角形的大小怎样变化，任何两边之比都是一个定值，然后为后面研究“两边的比值随角度变化”服务. 奠定这个基础应坚持一个原则，即教师作图，学生观察，教师引导学生分析，由学生自己得出结论. 切忌教师代替学生思考，切忌由教师得出结论. 试想，如果学生连这个基础都没奠定，那后面研究变化的过程时该从何谈起？

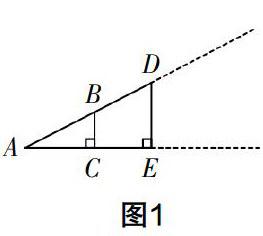
这个过程可以这样处理：教师先给出图1，从静态的角度观察图1，引导学生做出如下推理.

在Rt△ABC和Rt△ADE中，因为∠A=∠A，∠ACB=∠AED=90°，所以△ABC∽△ADE. 所以AE/AC=DE/BC. 不妨设AE/AC=DE/BC=k，k为相似比，则AE=kAC，DE=kBC. 所以DE/AC=kBC/kAC=BC/AC.

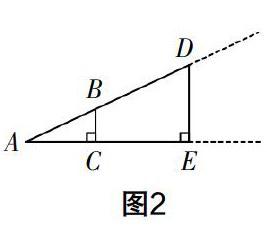
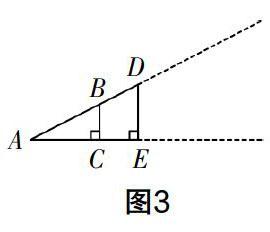
在图1的基础上，教师再给出图2和图3，保持Rt△ABC的大小不变，从动态的角度观察图形，引导学生认识到Rt△ADE的大小在不断地变化. 图2中的Rt△ADE在图1的基础上放大，图3中的Rt△ADE在图1的基础上缩小. 研究发现，无论Rt△ADE是放大，还是缩小，DE/AC的值总等于BC/AC的值. 因为在整个变化的过程中，Rt△ABC的大小保持不变，所以BC/AC的值不会变. 于是可以得出结论：在直角三角形中，当锐角一定时，无论三角形的大小怎样变化，这个锐角的对边与邻边的比是一个定值.

如果有条件，上述过程可借助几何画板、动态作图来教学，这样的话，学生可以直接参与操作，易于理解和接受;不具备现代教学条件的，教师要在黑板上画图，但画图时必须体现图形的动态变化.

从一个点突破

在直角三角形中，边与边的情况有好几种，选择一种情况来突破，不仅效果好，而且效率高. 这是因为：（1）几种情况一起讲，难以讲清楚. 即使能讲清楚，容易相互干扰，学生也难以全部接受，倒不如抓住一种情况来进行教学. （2）锐角三角函数的几种对应关系很类似，所以可以根据前面奠定的基础，选择一种情形来突破. 比如，前面已经奠定“在直角三角形中，当锐角一定时，无论三角形的大小怎样变化，这个锐角的对边与邻边的比是一个定值”这一基础，此时就可以选择“对边比邻边”来进行教学.

体现“函数味”

在初中函数教学中，我们应培育学生树立相互联系、运动发展的数学理念，在动态的思维模式中掌握函数知识的基本要领. 函数的本质是描述在一个变化的过程中，两个变量之间紧密关联、相互依存的关系，一个变量随着另一个变量的变化而发生变化. 不妨设其中一个变量为x，另一个变量为y，对于每一个x，y都有唯一的值与之对应，则y是x的函数，其中x是自变量，y是因变量.

在初中数学锐角三角函数中，哪个是自变量，哪个是因变量呢？我们还是先引领学生观察变化过程. 教师给出图4，因为“在直角三角形中，当锐角一定时，无论三角形的大小怎样变化，这个锐角的对边与邻边的比是一个定值”，即边的比值与直角三角形的大小无关. 为了研究方便，不妨把AC的长度固定下来，这样BC/AC的值就取决于BC的大小. 因为是研究变化过程，所以以图4为基础图，从动态角度去作图：图4中的点B是控制点，可以上下拖动，从而改变直角三角形中的元素. 在图4的基础上，将点B往上拖（如图5），此时∠BAC变大，BC边变长;将点B往下拖（如图6），此时∠BAC变小，BC边变短. 在拖动点B的变化过程中，只要点B的位置改变，∠BAC的大小就会发生改变，BC边的长也发生改变. 而且，对于∠BAC的任何一个大小，BC边都有唯一的长度与之对应. 此时，可引导学生完整地表述：在这个变化过程中，BC/AC的值随着∠BAC的变化而变化，且对于∠BAC的任何一个值，BC/AC都有唯一的值与之对应（可见，符合函数定义），所以BC/AC是∠BAC的函数. 这里可以考虑向学生指出：在这个变化的过程中，BC/AC是创造的变量，原本的变化过程中并没有这个变量.

接着引导学生思考：怎样表示刚才发现的这个函数关系呢？接下来再引出：数学中规定，用“tan∠BAC=BC/AC”来表示这种关系. 在∠BAC不引起歧义的前提下，还可以去掉角的符号和另外两个字母，直接表示为“tanA=BC/AC”. 此时，可以由学生自己判断，在这个函数关系中，哪个是自变量，哪个是因变量.

以点带面

在讲清正切函数的基础上指出正弦函数、余弦函数与正切函数类似，只是“不同的边进行相比”，再给正弦函数、余弦函数下定义. 这种以点带面的处理方式，一是思路清晰，教法干练;二是高效，避免重复啰唆;三是符合人类认知事物的一般规律，还能发展学生的类比分析能力.

概念巩固

概念巩固通常需要从正、反两方面来加强. 对于锐角三角函数的正面加强，可以考虑如下方式：（1）解释概念名称. 比如解释“正切”可以这样处理：“正”，是指角正对的边，即对边，“切”，可让学生联想在家做饭时切菜的姿势，与菜斜着时用刀，叫“削”，与菜垂直时用刀，叫“切”，所以“切”表示“垂直关系”. 这样既生动形象，又与学生的实际生活联系了起来.（2）正面应用定义，利用定义来解题. 比如计算30°等特殊角的三角函数值.

对于锐角三角函数概念的反面加强，常用的方法是给出错误的应用，讓学生去分析、判断. 比如如图7，在Rt△ABC中，∠C=90°，AB=10 cm，BC=6 cm，请判断下面的说法是否正确：①sinB=AC/AB;②sinA=0.6 cm. 比如如图8，∠ABC≠90°，请判断sinA=BC/AC是否正确. 比如如图9，Rt△DEF∽Rt△ABC，且相似比k=DE/AB=2，请判断sinB=1/2sinE是否正确.

这种锐角三角函数教学处理方式，注重数学知识本身的特性，注重学生思维品质的培养，注重学生能力的发展，不仅能引导初中生对三角函数有一个清晰、准确的认识，而且能为高中学习任意三角函数知识积累研究经验，打下坚实的理论基础.