时滞扰动类Lorenz系统的Hopf分岔

李文娟, 牛潇萌, 李旭超, 俞元洪

(1.赤峰学院数学与统计学院,内蒙古 赤峰 024000;2.赤峰学院计算机与信息工程学院,内蒙古 赤峰 024000);

时滞扰动类Lorenz系统的Hopf分岔

李文娟1, 牛潇萌1, 李旭超2, 俞元洪2

(1.赤峰学院数学与统计学院,内蒙古 赤峰 024000;2.赤峰学院计算机与信息工程学院,内蒙古 赤峰 024000);

通过非线性动力学理论,对时滞类 Lorenz系统在平衡点的稳定性问题和发生Hopf分岔的条件进行了研究.首先计算得到系统的平衡点,然后通过分析系统在平衡点处的相应特征方程根的分布,得到系统在平衡点局部渐近稳定和产生Hopf分岔的时滞临界点.以时滞为分叉参数,研究了时滞系统存在Hopf分岔的条件.最后,利用Matlab程序进行仿真验证所得结论与理论分析一致.本文的结论是对一些已有文献研究成果的推广.

时滞;类Lorenz系统;稳定性;Hopf分岔

1 引言

自1963年,美国气象学家Lorenz在研究区域小气候时提出了第一个经典的Lorenz系统[1]以来,混沌系统得到了更广泛的研究和应用.此系统在混沌学历史上有着重要的地位,特别是对它的分析在了解非线性方程如何出现混沌解方面很有意义.随着对Lorenz系统研究的不断深入,各种新的类Lorenz混沌系统大量产生,这种新的类Lorenz混沌系统在保密通信、激光物理、控制工程、化学反应和生物医学等领域应用广泛[2-4].现有的各种新的类Lorenz混沌系统仍无法满足各领域应用的需要,于是人们开始寻找新的类Lorenz混沌系统,在此期间,很多学者得到一些行为复杂的系统,例如Chen系统、Lu系统、Liu系统、Qi系统、Chua系统等[5-9].但是上述研究主要是混沌的同步和控制,对分岔的研究相对较少.对于时滞类Lorenz系统的研究更是不多.

2015年,文献[10]提出了一类新的类Lorenz系统

其中x,y,z是状态变量，a,b,c,d为系统参数．2015年,文献[11]提出了一类带时滞的类Lorenz系统

其中x,y,z是状态变量;a,b,c,d为系统参数;τ＞0为系统常量时滞．

本文的主要结果是将文献[11]的系统(2)中第一个非线性方程中的a(y−x)改为

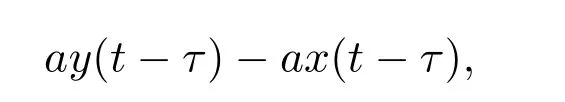
第二个非线性方程中的bx(t−τ)改为bx,第三个非线性方程中的dx2改为

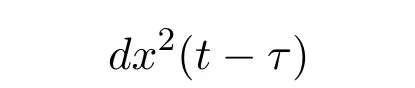
得到一类新的双时滞类Lorenz系统.通过对一类新的双时滞类Lorenz系统在零平衡点的线性化系统的特征方程的分析给出该系统在零平衡点的稳定性问题和发生Hopf分岔的条件.最后通过数值拟真验证所得结论的正确性.本文研究的是双时滞类Lorenz系统,文献[10]研究的是没有时滞的类Lorenz系统,文献[11]研究的是单时滞的类Lorenz系统.当本文中的时滞为零时即为文献[10]研究的系统.

2 主要结果及证明

本文考虑时滞类Lorenz系统:

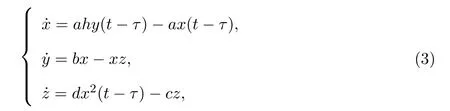
其中x,y,z是状态变量;a,b,c,d,h为系统参数;τ＞0为系统常量时滞,可理解为信号传输的阻碍时间等.设系统参数

系统(3)的平衡点满足下列条件:

由(4)式知系统(3)的平衡点有三个,它们分别为

2.1 平衡点稳定性分析

定理 2.1假设τ=0,则系统(3)在平衡点

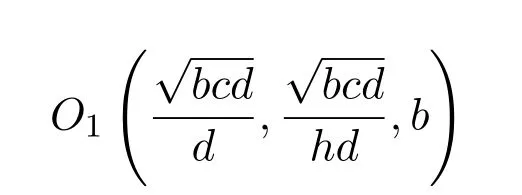
处是不稳定的.

证明在平衡点

处,系统(3)的Jacobian矩阵为:

矩阵(5)对应的特征方程为:

即

其中

当τ=0时,(6)式转化为

因为系统参数 a＞0,b＜0,c＞0,d＞0,h＞0,所以 2abch＜0根据罗斯 -霍维兹(Routh-Hurwitz)判据可知,(7)式的特征根具有正实部.所以当τ=0时,系统(3)在平衡点

处是不稳定的.

注 2.1因为在变换S:(x,y,z)−→(−x,−y,z)的作用下具有不变性,即关于z具有对称性.所以只讨论系统(3)在平衡点

的稳定性.

下面讨论在平衡点O(0,0,0)处的稳定性.在平衡点O(0,0,0)处易求得线性化系统

线性化系统(8)对应的特征方程为

特征方程(9)可化为

其中

引理 2.1假设τ=0,则系统(3)在平衡点O(0,0,0)处是渐近稳定的.

证明当τ=0时,(10)式转化为

因为系统参数a＞0,b＜0,c＞0,d＞0,h＞0,所以(a+c)＞0,−abch＞0且有

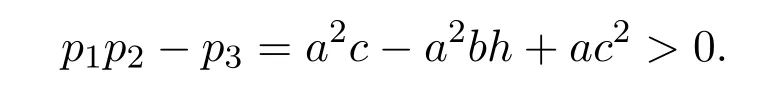
根据罗斯 -霍维兹 (Routh-Hurwitz)判据可知,(11)式的所有特征根都具有负实部.所以当τ=0时,系统(3)在平衡点O(0,0,0)处是局部渐近稳定的.

2.2 Hopf分岔问题

接下来讨论在平衡点O(0,0,0)处的Hopf分岔存在的条件.

当τ＞0时,由于只考虑虚根,方程(10)等价于下面方程

设λ=iω(ω是大于零的常数）是(10)式的一个纯虚根,则虚部ω满足

根据复数相等可得

由三角函数的等式推得(13)式可化为

对(14)式有以下结论.

引理 2.2(14)式至少有一个正实根.

证明令u=ω2,则式(14)可化为

设

由(16)式得

根据函数零点存在定理,至少存在一个实数u0∈(0,+∞),使得f(uo)=0.所以(15)式至少有一个正实根．因为u=ω2,从而(14)式至少有一个正实根.

设ω0为(14)式的正实根,则(10)式有一纯虚根iω0.又由(13)式得

将ω=ω0代入方程(17),则时滞τ的值为

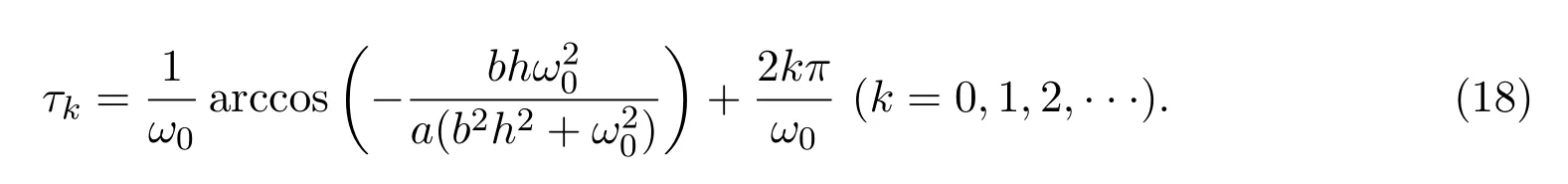
因此 (iω0,τk)是 (10)式的解,即当时滞 τ=τk时,λ=±iω0是 (10)式的一对共轭的纯虚根.

设τ0=min{τk},则时滞τ=τ0是(10)式出现纯虚根λ=±iω0时τ的最小值.故可得如下的引理3.

引理2.3如果

那么(10)式有一对纯虚根

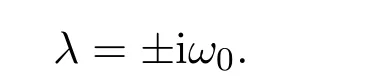
设(10)式的特征根

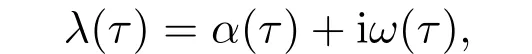
满足

引理 2.4对于任意的τ=τk/=0,则

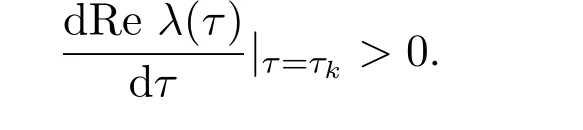
证明对(10)式两边关于τ求导，可得

由(10)式可得

易得

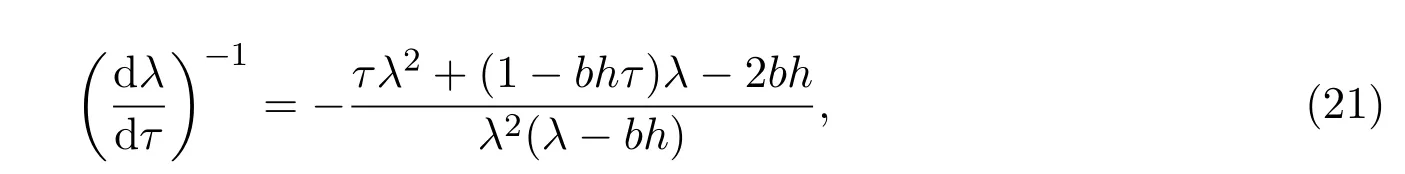
由(21)式和

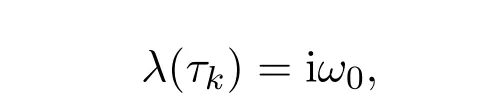
可得

由于

同号.证毕.

根据引理2.1-引理2.4和Hopf分岔理论可得下面结论．

定理2.2如果

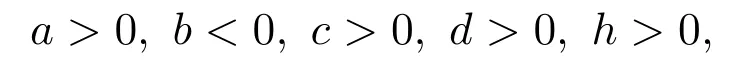
那么

(1)当τ∈[0,τ0)时,系统(3)在平衡点O(0,0,0)是渐近稳定的;

(2)当τ＞τ0时,系统(3)在平衡点O(0,0,0)是不稳定的;

(3)当

时,系统(3)在平衡点O(0,0,0)处发生Hopf分岔,产生极限环.

注 2.2定理的结论可以由下部分的数值仿真来验证.文献[1]的系统是系统(3)中

时的特例.此外,定理也推广了文献[2]的结果.

3 数值仿真

时滞类Lorenz系统(3)的参数a＞0,b＜0,c＞0,d＞0,令

这时系统(3)可化为

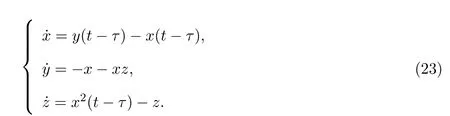
利用Matlab软件计算得(11)式的正实根

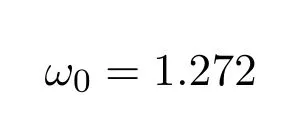
和(15)式中

故,由定理可得下面的推论.

推论3.1如果

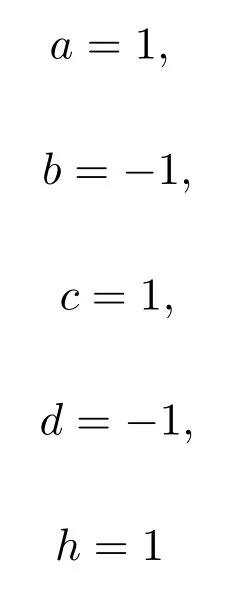
则

(1)当τ∈[0,0.7111)时,系统(23)在平衡点O(0,0,0)是渐近稳定的;

(2)当τ＞0.7111时,系统(23)在平衡点O(0,0,0)是不稳定的;

(3)当

时,系统(23)在平衡点O(0,0,0)处发生Hopf分岔,产生极限环.

下面用Matlab软件绘出时滞τ取不同值时,系统(23)的状态变量随时间t的轨线图和相图,验证所得结论的正确性.

图1-1 时滞τ=0.7时,系统(23)的状态 变量x随时间t的轨线图

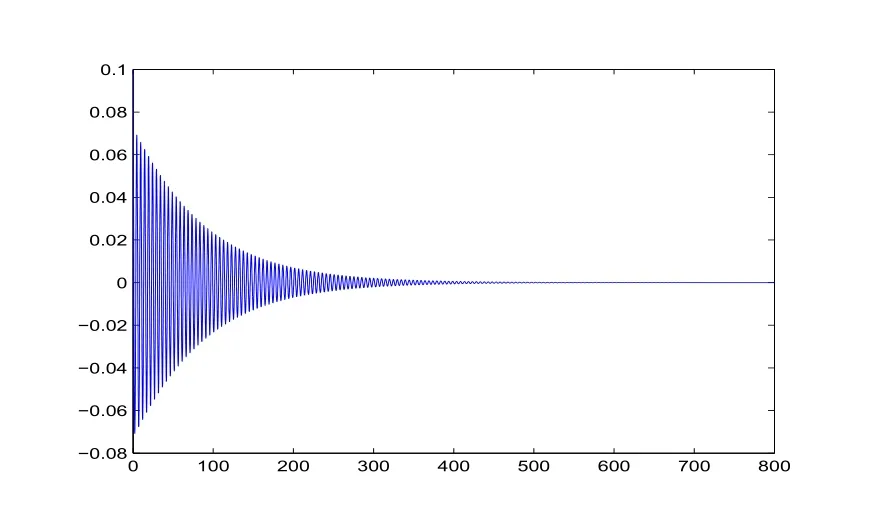
图1-2 时滞τ=0.7时,系统(23)的状态 变量y随时间t的轨线图

图1-3 时滞τ=0.7时,系统(23)的状态 变量z随时间t的轨线图

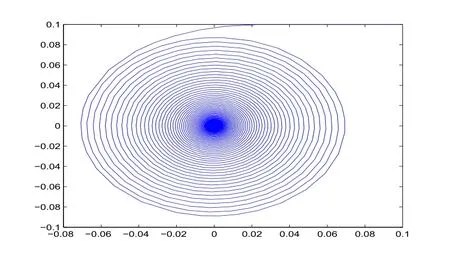
图1-4 滞τ=0.7时,系统(23)的状态 在xoy平面内的相图

从图 1-1、图1-2、图1-3可以看出，当时滞τ=0.7时,系统(23)的状态变量x,y,z的值随时间t的增大而趋于平衡点O(0,0,0),所以系统(23)在平衡点O(0,0,0)是渐近稳定的．

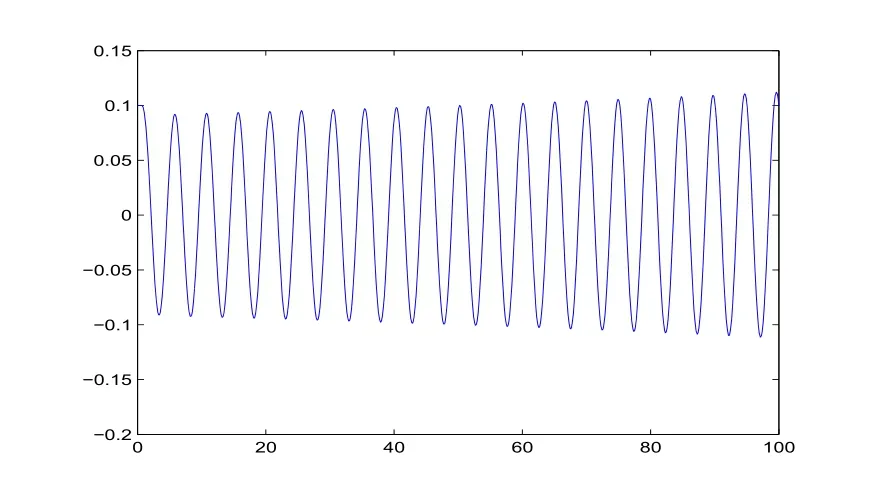
图2-1 时滞τ=0.7111时,系统(23)的状态变量x随时间t的轨线图

图2-2 时滞τ=0.7111时,系统(23)的状态 变量y随时间t的轨线图

图2-3 时滞τ=0.7111时,系统(23)的状态}变量z随时间t的轨线图

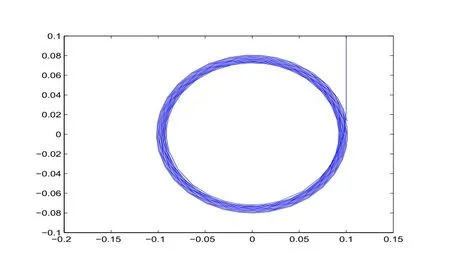
图2-4 时滞τ=0.7111时,系统(23)的状态 在xoy平面内的相图

从图2-1、图 2-2、图 2-3可以看出,当时滞 τ=0.7111时,系统(23)的状态变量 x,y,z的值随时间t的增大保持等周期震荡,所以系统(23)在平衡点O(0,0,0)处发生Hopf分岔,产生极限环.

图3-1 时滞 τ=0.72时,系统(23)的状态变量x随时间t的轨线图

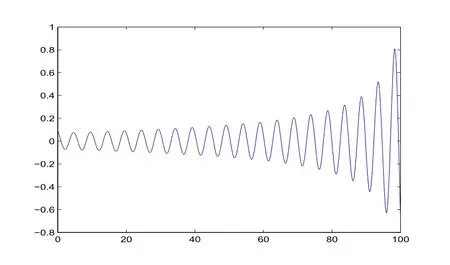
图3-2 时滞τ=0.72时,系统(23)的状态 变量y随时间t的轨线图

图3-3 时滞 τ=0.72时,系统(23)的状态 变量z随时间t的轨线图

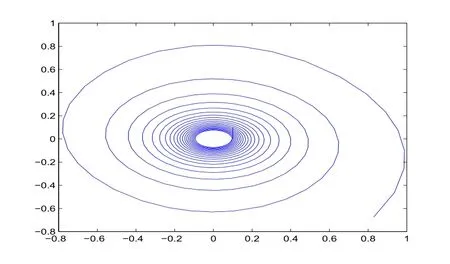
图3-4 时滞τ=0.72时,系统(23)在xoy平面里的相图

从图3-1、图3-2、图3-3可以看出,当时滞τ=0.72时,系统(23)的状态变量x,y,z的值随时间t的增大而逐渐远离平衡点O(0,0,0),说明系统(23)在平衡点O(0,0,0)是不稳定的.

图 1-4、图 2-4、图 3-4可以看出,当时滞 τ＜τ0,τ=τ0,τ＞τ0时,系统 (23)xoy平面内的相图.

[1]Lorenz E N.Deterministic non-periodic fl ows[J].J.Atmos.Sci.,1963,20:130-141.

[2]刘式适,刘式达.物理学中的非线性方程[M].北京:北京大学出版社,2012:341-345.

[3]王兴元.混沌系统的同步及在保密通讯中的应用[M].北京:科学出版社,2012:356-385.

[4]刘扬正.超混沌Lü系统的电路实现[J].物理学报,2008,57(3):1439-1443.

[5]Wenxin Q,Gangrong C.On the boundedness of solutions of the Chen system[J].J.Math.Anal.Appl.,2007,329(1):445-451.

[6]Mkaouar H,Boubaker O.Chaos synchronization for master slave piecewise linear systems application to Chua’s circuit[J].Commun Nonlinear Sci.Numer Simulat.,2012,17(3):1292-1302.

[7]Chongxin L,Tao L,Ling L,et al.A new chaotic attractor[J].Chaos,Solitons and Fractals,2004,22:1031-1038.

[8]Yongguang Y,Suochun Z.Hopf bifurcation in the Lü system[J].Chaos,Solitons and Fractals,2003,17(5):901-906.

[9]Guoyuan Q,Gangrong C,Shengzhi D,et al.Analysis of a new chaotic system[J].Physica A,2005,352:295-308.

[10]官国荣,吴成茂,贾倩.一种改进的高性能Lorenz系统构造及其应用[J].物理学报,2015,64(2):1-14.

[11]李德奎,连玉平.单时滞类Lorenz系统的Hopf分岔分析[J].数学杂志,2015,35(3):633-642.

Hopf bifurcation analysis of the disturbed Lorenz-like System with the delayed

Li Wenjuan1,Niu Xiaomeng1,Li Xvchao2,Yu Yuanhong3
(1.School of Mathematics and Statistics,Chifeng University,Chifeng 024000,China;2.Computer and Information Technology Institute,Chifeng University,Chifeng 024000,China;3.Academy of Mathematics System Sciences,Chinese Academy of Sciences,Beijing 100190,China)

In this paper,we analyze the stability and Hopf bifurcation condition of the system at its balance by using the nonlinear dynamics theory.The equilibrium point is obtained and then critical point of the delay for local stability of the equilibrium and existence of local Hopf bifurcation is also obtained by analyzing distribution of roots of the corresponding characteristic equation.the condition for the existence of Hopf bifurcation of this delay system is studied by taking delay as bifurcation parameter.Furthermore,by Matlab program some numerical simulations were given to show the correctness of the obtained conclusion.This paper extends the research achievements in the cited literature.

time-delay,Lorenz-like system,stability,Hopf bifurcation

O175

A

1008-5513(2017)05-0475-11

10.3969/j.issn.1008-5513.2017.05.005

2017-03-27.

国家自然科学基金(11561001);内蒙古自然科学基金(2014MS0101);内蒙古高等学校科研基金（NJZY17301).

李文娟(1981-),硕士,讲师,研究方向：稳定性理论及应用.

2010 MSC:34C10,34C15