带双参数的a,b无限维李代数W(a,b)的性质

余德民, 方春华, 王春辉

(1.湖南理工学院数学学院,湖南 岳阳 414000;2.岳阳市第十三中学,湖南 岳阳 414000)

带双参数的a,b无限维李代数W(a,b)的性质

余德民1, 方春华1, 王春辉2

(1.湖南理工学院数学学院,湖南 岳阳 414000;2.岳阳市第十三中学,湖南 岳阳 414000)

研究了带双参数的a,b的无限维W(a,b)型李代数,这类李代数是Virasoro李代数的推广.本文研究了这类李代数的两类子代数,一类子代数同构无中心的Virasoro李代数,另一类子代数是交换李子代数,并且是理想.研究了这类李代数同构和同态,证明了g不是单李代数.

李代数;同构;同态

1 引言

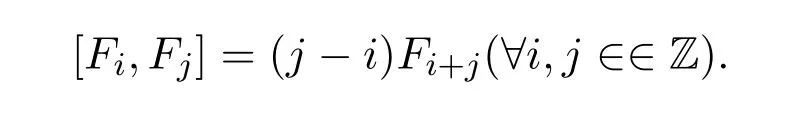
vir为单李代数.本文研究一类单带双参数的 a,b无限维 W(a,b)型李代数g,这类李代数是Virasoro李代数的推广,g为C上线性空间,其基向量为Li,Wj(∀i,j∈Z),张成的复数域C上的线性空间，李运算定义如下：

此运算在基向量上线性扩张,其中 a,b为复数,并满足反对称性和Jacobi不等式,称 g为带双参数的a,b无限维李代数W(a,b),苏育才教授研究了无限维李代数 W(a,b)的中间系列模(文献[1]),许萤博士研究了双参数的a,b无限维李代数 W(a,b)的表示 (文献 [2]).本文作者曾研究了Virasoro李代数及其推广的Virasoro李代数(文献[3-7]),夏春光博士研究了推广的Virasoro李代数的结构分类,导子和自同构和最高权模(文献[8-10]).本文研究了这类李代数的子代数,同构和同态.

2 主要结果

设由 Li(∀i∈Z)张成的子空间为g1.

定理 2.1g1是g的无限维非交换子代数.

证明∀i,j∈Z,可验证

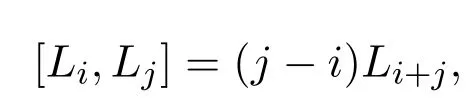
从而,g1是g的子代数,g1也是g的无限维非交换子代数.构造g1到映射如下:φ1在g1的基向量Li上线性扩张.

定理 2 .2φ1是 g1到的同构.

证明从构造知φ1是g1到同构的线性映射,且既是单射.可验证

从而 φ1是 g1到的同构.

从同构的意义上说,无中心的Virasoro李代数(以后简化为),是无限维李代数W(a,b)的子代数,也可以说无限维李代数W(a,b)的子代数是无中心的Virasoro李代数(以后简化为)的推广.

设由 Wi(∀i∈Z)张成的子空间为g2.

定理 2 .3g2是g的无限维交换子代数,并且是g2是g的理想,从而g不是单李代数.

证明∀i,j∈ Z ,由于

从而,g2是g的无限维交换子代数,∀i,j∈Z,由于

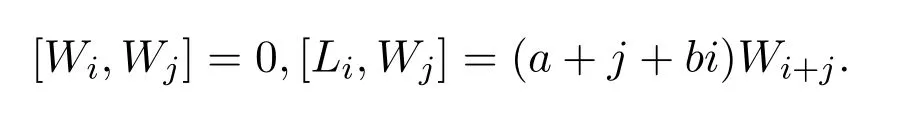
从而g2是g的理想,从而g不是单李代数.

构造g到g映射如下:

φ2在g的基向量Wj,Li上线性扩张.

定理2.4φ2是 g到 g的同构.

证明从构造知φ2是g到g同构的线性映射,且既是单射.可验证

从而 ∀u,v∈g,

则φ3是g到g的同构.当参数

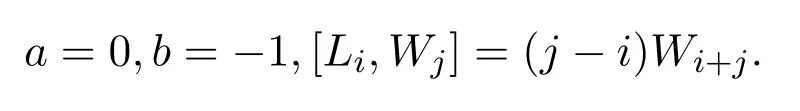
构造g到g映射如下:

φ3在g的基向量Wj,Li上线性扩张.

定理2.5当参数φ3是g到g的单同态,其中当 n=−1,φ3是 g到 g的同构.

证明从构造知φ3是g到g同构的线性映射,且既是单射.可验证

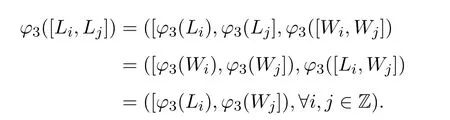
从而 ∀u,v∈g,

则φ3是g到g的单同态.当n=−1,φ3是g到g的同构.

3 结论

本文首先定义了带双参数的a,b的无限维W(a,b)李代数,证明了g2是g的无限维交换子代数,并且是g2是g的理想,并用比较强的技巧构造φ2是g到g的同构,以后将研究无限维李代数W(a,b)的表示理论.

[1]Yucai Su,Ying Xu,Xiaoqing Yue.Indecomposable module of the immediate series over W(a,b)algebra[J].Science China Mathematics 2014,57(2):276-291.

[2]许萤.扩张仿射李代数的双代数结构和W(a,b)李代数的表示[D].合肥:中国科学技术大学,2012.

[3]余德民,梅超群.一类无限维半单李代数[J].系统科学与数学:中文版,2008,28(9):1101-1108.

[4]余德民,卢才辉.李代数L(Z,f,δ)的特殊性质[J].数学进展,2006,35(6):707-711.

[5]余德民,卢才辉.Virasoro李代数的子代数若干结果[J].数学学报:中文版,2006,49(3):633-638.

[6]余德民,卢才辉.Virasoro李代数的子代数的同构及生成元[J].系统科学与数学:中文版,2008,28(1):24-29.

[7]余德民,梅超群,郭晋云.一些特殊项链李代数的同态[J].数学年刊:中文版,2009,30(4):551-562.

[8]Xia C,You T,Zhou L.Structure of a class of Lie algebra of Block type[J].Comm.Algebra,2012,40:3113-3126.

[9]Xia C,Wang W.Derations and automorphisms of a Lie algebra of Block type[J].Algebra Colloq.,2013,20:173-180.

[10]Xia C,Zhang R.Unitary quasi fi niti high weight modules over Block type Lie algebra B(q)[J].J.Lie algebra,2013,23:159-176.

Property of an new in fi nite dimensional W(a,b)Lie algebra with parameter a,b

Yu Deming1,Fang Chunhua1,Wang Chunhui2
(1.College of Mathematics,Hunnan Institute of Science and Technology,Yueyang 414000,China;2.Thirteen Middle School in Yueyang,Yueyang 414000,China)

In this paper,In fi nite dimensional Lie algebra W(a,b)with two parameter a,b is constructed and the in fi nite dimensional lie algebra is a generalization of Virasoro-like Lie algebra.Two Subalgebra are studied.One is isomorphic to Virasoro Lie algebra with no central.The other is abelian and the other is ideal.Isomorphisms and homomorphism of the in fi nite dimensional Lie algebra are studied.We prove that it is not a simple Lie algebra.

Lie algebra,isomorphisms,homomorphisms

O152.5

A

1008-5513(2017)05-0462-04

10.3969/j.issn.1008-5513.2017.05.003

2017-03-10.

国家自然科学基金(11771135);湖南省社科基金教育学专项课题(XSJ17B16);湖南省省级教研教改项目(缃教通(2016)400)).

余德民(1975-),博士,副教授,研究方向：李代数.

方春华(1979-),博士,副教授,研究方向：计算数学.

2010 MSC:17B05,17B40