带有R-S积分边值条件的分数阶朗之万方程的解的存在性

王西丽, 周宗福

(安徽大学数学科学学院,安徽 合肥 230601)

带有R-S积分边值条件的分数阶朗之万方程的解的存在性

王西丽, 周宗福

(安徽大学数学科学学院,安徽 合肥 230601)

研究一类带有 R-S积分边值条件的非线性分数阶朗之万方程边值问题.利用Leray-Schauder非线性抉择和Leray-Schauder度理论,得到几个新的存在性结果.最后给出一个例子来证明主要结论的应用性.

分数阶朗之万方程;积分边值条件;Leray-Schauder度理论;Leray-Schauder非线性抉择

1 引言

朗之万方程是由朗之万在1908年描述布朗运动时提出的[1].在他的著作中牛顿第二定律应用于布朗粒子时的随机物理运动称之为朗之万方程.朗之万方程已经被广泛的用来描述波动环境下的物理现象的演化[2].分数阶朗之万方程可以看作是整数阶朗之万方程的拓展,现在已经成为微分方程的研究热点[3-5].近来,分数阶微分方程的问题引起了许多专家的兴趣[6-7].

2012年,文献[8]研究了三点边值问题的朗之万方程的解的存在性:其中0＜α≤1,1＜β≤2,和是开普特分数阶导数,λ是实数.利用压缩映射原理和Guo-Krasnoselskii锥不动点定理,得到几个解的存在性证明.

2016年,文献[9]研究了下列的分数阶朗之万方程的无穷多点边值问题:

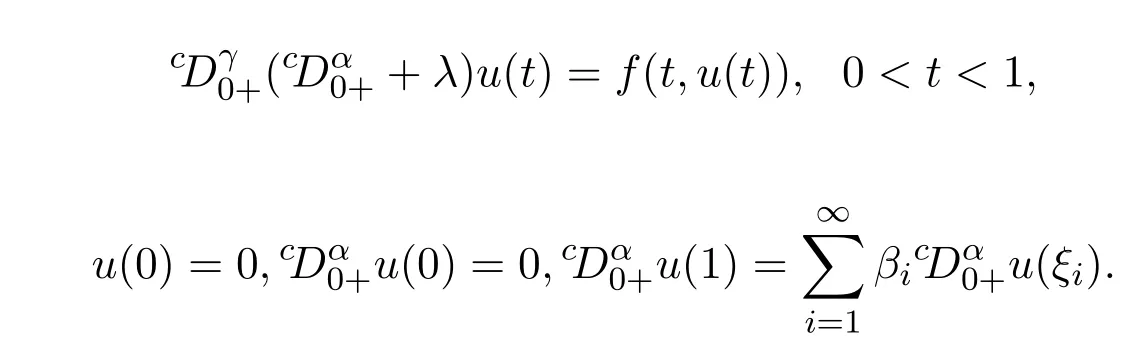
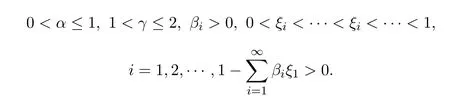
利用Leray-Schauder非线性抉择和Leray-Schauder度理论可以得到一个独特的满足上述开普特分数阶微分方程边值问题解的存在性.

是连续不减的.

本文利用Leray–Schauder非线性抉择和Leray–Schauder度理论研究以下的带有R-S积分边界条件的分数阶朗之万方程边值问题,得到此边值问题(1)和边值问题(2)的解存在性的若干结果[11-12].

2 预备知识

定理 2.1Riemann-Liouville分数阶积分算子的阶q＞0,函数x(t)存在以下定义:

定理 2.2秩为q的分数阶开普特微分方程,有连续可微的函数x:[0,+∞]→R,存在如下定义:

其中

并且[q]表示q的整数部分.

引理 2.1令,则u(t)是如下分数阶朗之万微分方程线性边值问题:

的解的充分必要条件是

证明由于1＜γ≤2,故由以及(3)引理(2.1)可知,

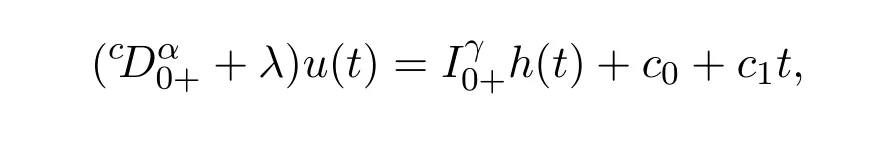
其中 c0,c1∈R.

因此,

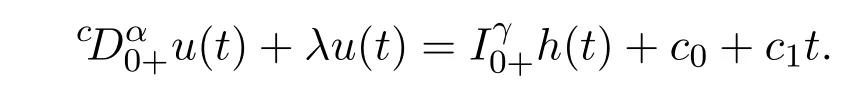
同理,由于0＜α＜1可得

其中c2∈R.

由边值条件u(0)=0,所以可以得到c2=0.因此,方程存在通解(3)满足:

由边值条件

可得

并且

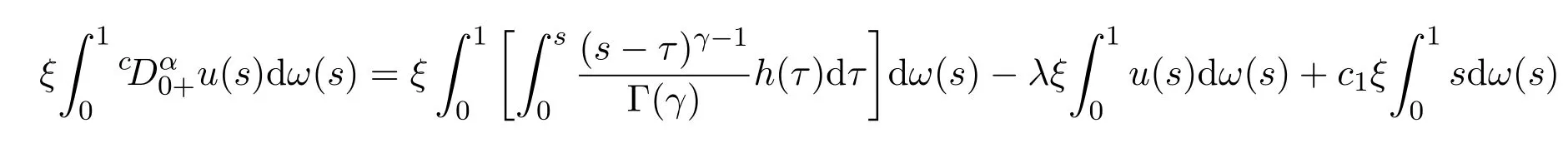
因此可知

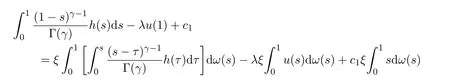
从而推导出

所以,u(t)满足:

相反的,如果u(t)满足(5),则

其中

可得

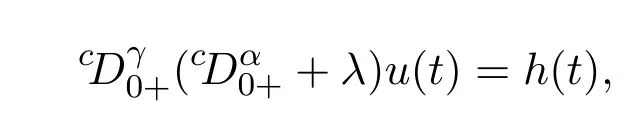
可见u(t)满足(5).

进一步,有故u(t)满足(4)所以u(t)是问题(3)-(4)的解.证毕.

引理 2 .2设E是一个Banach空间,假设C⊂E是一个凸闭集.若U是一个相对于C的开子集,其中0∈U并且T:→E是一个全连续映射,T()有界.假设∀λ∈(0,1),u∈∂U,有 u /=θTU,则 T 在上至少有一个不动点.

3 主要结论

设E=C[0,1]是一个Banach空间,其中范数定义为:

定义映射T:E→E,

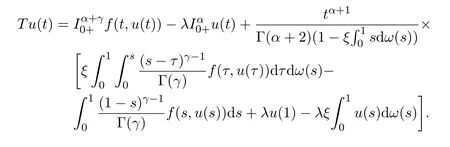
由引理2.2可得,当且仅当T有一个不动点时,u是边值问题(1)-问题(2)的解.记

现在我们利用Leray-Schauder非线性抉择来研究边值问题(1)-问题(2)的解的存在性.

定理3.1假设满足以下条件:

(H1)存在一个非负函数ω∈E使得在[0,1]的子集上满足ω＞0并且有一个不减的函数 φ:[0,∞)→[0,∞)使得 |f(t,u)|≤ω(t)φ(|u|),其中 (t,u)∈[0,1]×R;

(H2)存在M ＞0,使得

则边值问题(1)-问题(2)至少有一个解.

证明易得T是连续的.下面来证明T是将E上的有界集映射为有界集.对于任意数r＞0,Br={u∈E:‖u‖≤r}是E 上的有界集.则对于u∈Br,t∈[0,1],可得

因此

可见TBr有界.

接下来,证明T是将E上的有界集映射为等度连续的集合.对任意t2∈[0,1],其中,t1＜t2,

即知,当 t1→t2时,有

由Arzela-Ascoli定理,可以推导出T:E→E是全连续映射.设θ∈(0,1),u∈E可知u=θTu.由上述类似分析可知,

从而

故有

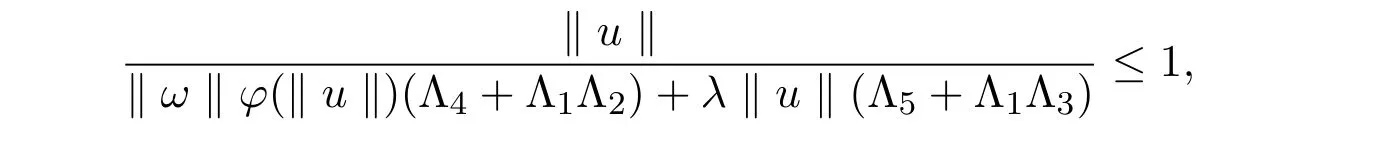
由(H2)以及上式可知,‖u‖/=M,令

则 ∀ u∈ ∂ UM,有 ‖ u‖=M,从而 ∀ u∈ ∂ UM,∀θ∈ ( 0,1),u/= θ Tu,可知 T :UM→E是全连续映射.因此,引理2.1能确保T至少有一个不动点u∈UM.所以边值问题(1)-问题(2)至少有一个解.证毕.

定理 3.2假设满足以下条件:

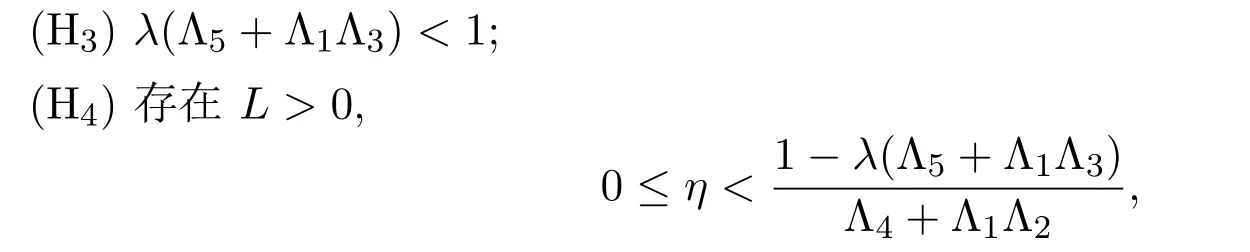
使得

都成立,则边值问题(1)-问题(2)至少有一个解.

证明考虑算子方程u=Tu.证明T至少有一个不动点u∈E.作

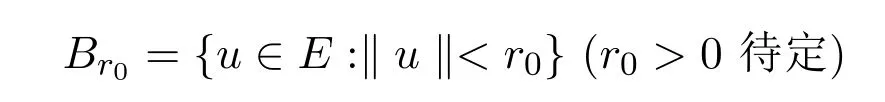
使得

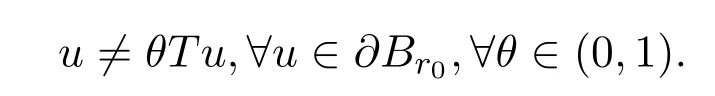
通过定理3.1的证明可知T是全连续的.令

由拓扑度的同伦不变性可知,

其中I定义为单位算子.

利用Leray-Schauder度的非零性,

在Br上至少存在一个解.

假设 u=θTu其中 u∈E,θ∈[0,1].则 ∀t∈[0,1],有

得到

因此

令

则对任一u∈∂Br0有u/=θTu并且θ∈(0,1).因此方程

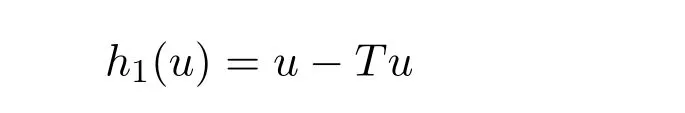
在Br0上至少有一个解.即T在Br上至少存在一个不动点,从而边值问题(1)-问题(2)至少有一个解.证毕.

4 实例应用

4.1 考虑下列的边值问题

其中

则有

选取

则

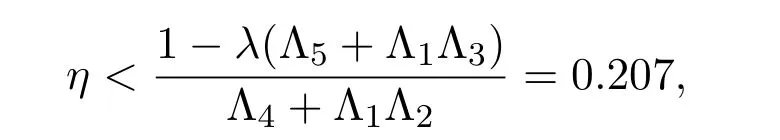
且对 (t,u)∈[0,1]×R有

从而定理3.2的条件都满足,故由定理3.2可知，边值问题(6)-问题(7)在[0,1]上至少有一个解.

[1]Langevin P.On the theory of Brownian motion[J].Comptes Rendusde Academie Bulgaredes Sciences,1908,146:515-530.

[2]Kubo R.The fuctuation-dissipation theorem[J].Rep.Prog.Phys.,1966,29:255-284.

[3]Burov S,Barkai E.Critical exponent of the fractional Langevin equation[J].Phys.Rev.Lett.,2008,100:590-601.

[4]Li B,Sun S,Li Y.Multi-point boundary value problems for a class of Riemann-Liouville fractional di ff erential equations[J].Adv.Di ff er.Equ.,2014,151:1-11.

[5]Zhang X.Positive solutions for a class of singular fractional di ff erential equation with in?nite-point boundary value conditions[J].Appl.Math.Lett.,2015,39:22-27.

[6]Yu T,Deng K,Luo M.Existence and uniqueness of solutions of initial value problems for nonlinear langevin equation involving two fractional orders[J].Commun.Nonlinear Sci.Numer.Simul,2014,19:1661-1668.

[7]Zhang X,Wang L,Sun Q.Existence of positive solutions for a class of nonlinear fractional di ff erential equations with integral boundary conditions and a parameter[J].Appl.Math.Comput,2014,226:708-718.

[8]Zhang X.Positive solutions for singular higher-order fractional di ff erential equations with nonlocal conditions[J].J.Appl.Math.Comput,2015,49:69-89.

[9]Yukunthorn W,Ntouyas S K,Tariboon J.Nonlinear fractional Caputo-Langevin equation with nonlocal Riemann-Liouville fractional integral conditions[J].Adv.Di ff er.Equ.,2014(3):315-330.

[10]Loghmani G,Javanmardi S.Numerical methods for sequential fractional di ff erential equations for Caputo operator[J].Bull.Malays.Math.Sci.Soc.,2012,35(2):315-323.

[11]Liu Z,Liang J.Multiple solutions of nonlinear boundary value problems for fractional di ff erential equations[J].Bull.Malays.Math.Sci.Soc.,2014,37(1):239-248.

[12]Momani S,Odibat Z.Numerical approach to di ff erential equations of fractional order[J].J.Comput.Appl.Math.,2007,207:96-110.

Existence of solutions for fractional-order Langevin equations with R-S Integral boundary conditions

Wang Xili,Zhou Zongfu
(School of Mathematical Sciences,Anhui University,Hefei230601,China)

In this paper,we investigate a class of boundary value problems of fractional-order Lengevinl equations with R-S Integral boundary conditions.By Leray-Schauder′s nonlinear alternative and Leray-Schauder degree theory,several new existence results of solutions are obtained.An example is given to show the applicability of our main results.

fractional-order Lengevinl equation,integral boundary value conditions,Leray-Schauder′s nonlinear alternative,Leray-Schauder degree theory

O175.8

A

1008-5513(2017)05-0486-10

10.3969/j.issn.1008-5513.2017.05.006

2017-10-12.

国家自然科学基金(11371027);安徽省自然科学基金(1608085MA12).

王西丽(1991-),硕士,研究方向：常微分方程边值问题.

周宗福(1964-),硕士,教授,研究方向：常微分方程边值问题.

2010 MSC:34B37,34B15