Rota-Baxter算子及其应用
2017-11-01周淑云
周淑云
(广东培正学院计算机科学与工程系,广东 广州 510830)
Rota-Baxter算子及其应用
周淑云
(广东培正学院计算机科学与工程系,广东 广州 510830)
Rota-Baxter算子是积分算子的抽象和推广.本文介绍了Rota-Baxter算子的概念和一些基本的性质,并且讨论了Rota-Baxter算子在序列、q-积分、矩阵代数等方面的应用.
Rota-Baxter算子;k-代数;交换环;矩阵
1 引言
设 k是一个交换环,Rota-Baxter代数是由一个结合的 k-代数和 Rota-Baxter算子组成,Rota-Baxter算子是积分算子的抽象和推广,包括求和、投影和数乘等算子,又作为经典的Yang-Baxter方程的算子形式被物理学家独立发现.Rota-Baxter代数的理论起源于美国数学家G.Baxter[1]于1960年的波动理论研究,接着Rota开始研究在组合学中的应用,他利用发生函数和Mobius反演公式得到了一系列的组合恒等式[2-3].近年来,Rota-Baxter代数得到了系统的发展,并在量子场论的重整化理论、树状代数、Hopf代数、哑积分、预Lie-代数、数论MZV及组合恒等式等理论中有着重要的应用[4-5].
在上世纪80年代,一些数学家在研究Yang-Baxter方程时,在Lie代数中发现了 Rota-Baxter恒等式,从而引起了很多数学家和物理学家的兴趣.1998年,Winkel[6]在研究Baxter序列方面的工作之后,Connes和Kreimer[7-8]于 2000年将 Rota-Baxter代数引入到量子域重正规化的研究,它是量子域重正规化理论从代数角度研究的奠基性工作.2000年,Guo利用Rota-Baxter代数研究了第一类和第二类Stirling数,指出了Rota-Baxter代数和分拆、多项式系数之间的联系[9].
Rota-Baxter代数与数学、数学物理有着十分紧密地联系,而且Rota-Baxter代数的研究与其它有着丰富成果的数学领域相比,还尚处在研究的初级阶段,所以有着十分广泛的研究与发展前景,见文献[5,10-13].
在第二节中,主要回顾了Rota-Baxter算子的定义及其基本性质,然后得到了一个构造权重为-1的Rota-Baxter算子的重要方法.第三节中,我们讨论了Rota-Baxter算子的一些重要的应用.
本文中的环R,是有单位元1R的交换环.我们用N表示自然数集构成的加法幺半群,N+表示正整数构成的加法半群,R表示实数域.文中有关的概念和记号均参见文献[5,13-14].
2 Rota-Baxter算子及其基本性质
设R是一个k-代数,如果R中的一个线性算子P:R→R满足Rota-Baxter程
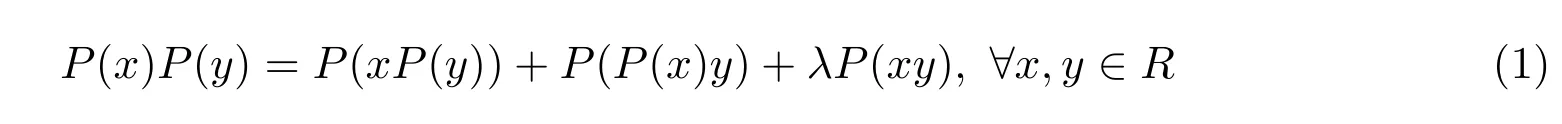
那么称P是R上的一个权重为λ的Rota-Baxter算子(简称RBO).其中λ∈k.
显然,0映射0:R→R是任意环R上的Rota-Baxter算子.因此每一个k-代数都可以看成是一个Rota-Baxter k-代数.单位映射IP显然是权重为−1的Rota-Baxter算子.
文献[14]中已初步讨论了Rota-Baxter算子的性质,下面我们进一步讨论它的性质,并利用RBO的性质得到一些Rota-Baxter算子的重要例子.
命题2.1[14](1)设(R,P)是Rota-Baxter代数,则P(R)是R的非酉子代数.
命题2.2[14]设 P 是权重为 − λ(或 λ)的Rota-Baxter算子,则P 也是权重为 − λ(或 λ )的Rota-Baxter算子.其中
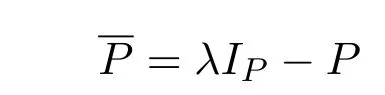
或

IP是单位映射.
定理2.1设R是一个k-代数,R上的线性算子P是权重为-1幂等的Rota-Baxter算子当且仅当存在R非酉的k-子代数R1,R2的k-模直和分解R=R1⊕R2,使得

是R到R1上的满射满足

证明如果R到非酉的k-子代数R1,R2有k-模直和分解R=R1⊕R2,则对于

有

则P是幂等的.
设
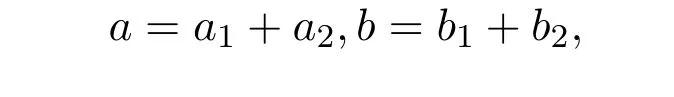
其中
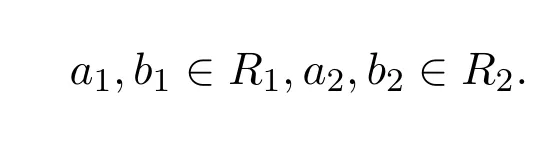
因为

所以

因此


得到
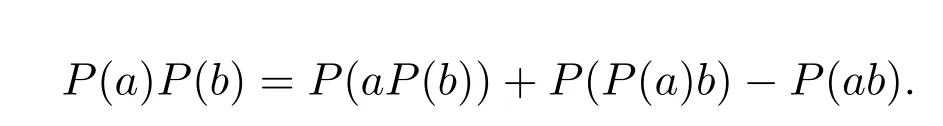
因此,P是权重为−1的幂等的Rota-Baxter算子.
反之,设P是权重为−1幂等的Rota-Baxter算子.令

且
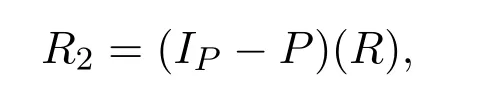
由命题2.1及2.2,得R1,R2是R非酉的k-子代数,且

因此

如果

则

所以

从而

又因为

是

的分解,所以P是R到R1上的满射.
3 Rota-Baxter算子的应用
下面讨论Rota-Baxter算子在矩阵代数、重正规化理论等方面的应用.
例3.1[5]设R是取值在k-上所有序列(an)n≥1之集.R上的运算按照分量相加、数乘及相乘构成一个k-代数,定义算子P为
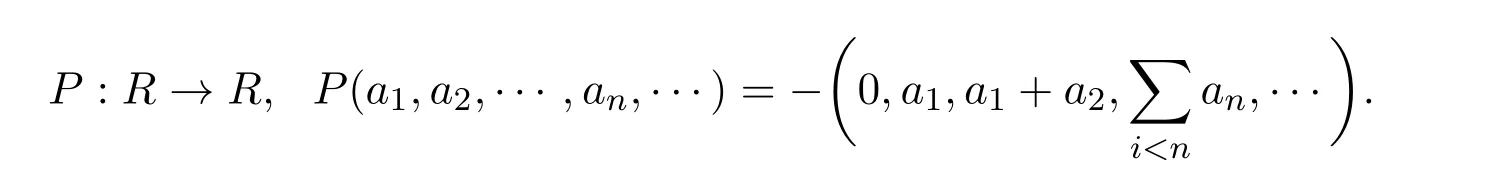
则P为R上权重为1的Rota-Baxter算子.
证明定义函数f:N≥0→R,则P(f)是部分和序列

对于f,g∈R,有

而

同理可证

则P满足等式(1),此时λ=1.
例3.2(q-积分)设R=K[t],q∈K 不是单位根.定义算子P为

即对于K[t]上的基tn,n≥1,有
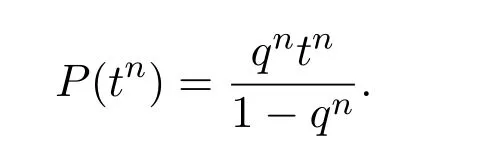
则P为R上权重为1的Rota-Baxter算子.
例3.3[5]设R,q如例3.2所述.定义R上的算子P为
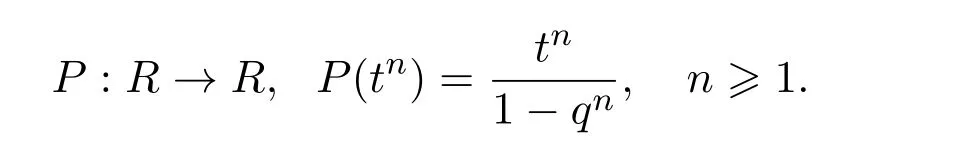
则P为R上权重为−1的Rota-Baxter算子.
证明因为

又

从而P为R上权重为−1的Rota-Baxter算子.
例3.4设n为正整数,R是环k上n阶下三角方阵构成的k-代数,令

其中

则P为R上权重为−1的Rota-Baxter算子.
证明设
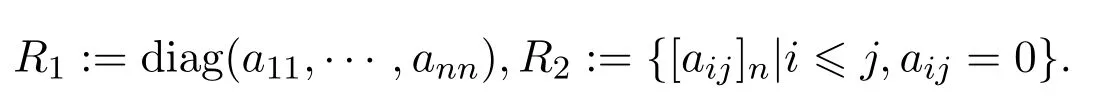
则R1,R2是 R的k-子代数,且

由定理2.3知,P为R上权重为−1的Rota-Baxter算子.
下面的例子说明Rota-Baxter算子在摄动量子域的重正规化理论中起着重要的作用.
例3.5[7-8](Laurent series[5])设K为域,R为Laurent series代数:
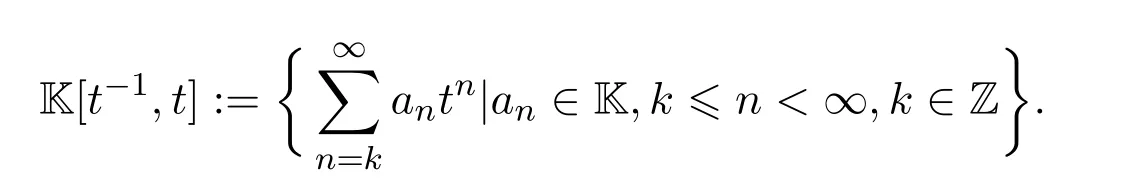
定义R上的算子P为:

且

规定空集上的和为零.及

且

则P和P都为R上权重为−1的Rota-Baxter算子.
证明设

则

其中
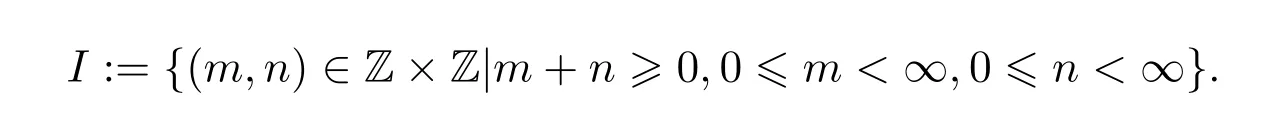
而

其中

同理

其中

由于

所以
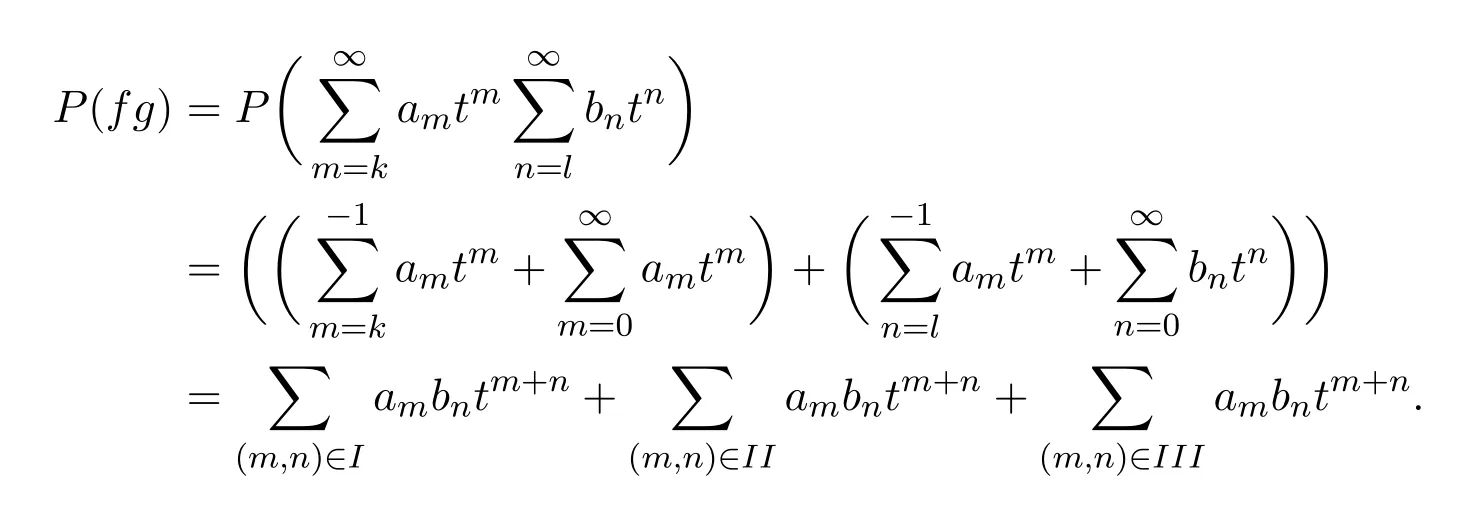
从而

由于

且

显然 R1∩R2=0,又
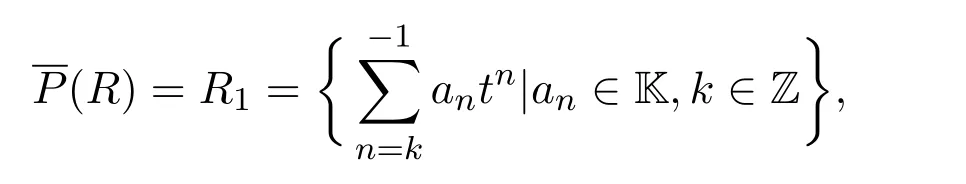
由定理2.3 P和P都为R上权重为−1的Rota-Baxter算子.
致谢:作者感谢国家留学基金委给予出国留学项目的资助,感谢美国Rutgers University at Newark及导师Guo.L..
[1]Baxter G.An analytic problem whose solution follows from a simple algebraic identity[J].Paci fi c J.Math.,1960(10):731-742.
[2]Rota G C.Baxter algebras and combinatorial identities I[J].Bull.Amer.Math.Soc.,1969(75):325-329.
[3]Rota G C.Baxter algebras and combinatorial identities II[J].Bull.Amer.Math.Soc.,1969(75):330-334.
[4]Ebrahimi-Fard K,Guo L,Kreimer D.Integrable renormalization II:the general case[J].Annales Henri Poincare,2005(6):369-395.
[5]Guo L.An Introduction to Rota-Baxter Algebra[M].China:Higher Education Press,2012.
[6]Winkel R.Sequences of symmetric polynomials and combinatorial properties of tableaux[J].Adv.Math.,1998,134:46-89.
[7]Connes A,Kreimer D.Renormalization in quantum fi eld theory and the Riemann-Hilbert problem.I:the Hopf algebra structure of graphs and main theorem[J].Comm.Math.Phys.,2000,210(1):249-273.
[8]Connes A,Kreimer D.Renormalization in quantum fi eld theory and the Riemann-Hilbert problem.II:the β-function,di ff eomorphisms and the renormalization group[J].Comm.Math.Phys.,2001,216(1):215-241.
[9]Guo L.Baxter Algebras,Stirling Numbers and Partitions[J].J.Algebra Appl.,2005(4):153-164.
[10]Rota G C,Smith D A.Fluctuation theory and Baxter algebras[J].Istituto Nazionale di Alta Mathematica,1972(IX):179-201.
[11]Guo L,Keigher W.On di ff erential Rota-Baxter algebras[J].J.Pure Appl.Algebra,2008(212):540-552.
[12]Keigher W.On the ring of Hurwitz series[J].Communications in Algebra,1997,25(6):1845-1859.
[13]Zhou S,Guo L.Rota-Baxter TD algebra and Quinquedendriform algebra[J].Algebra Colloquium,2017,24(1):53-74.
[14]周淑云.关于Rota-Baxter代数基本性质的探讨[J].青海师范大学学报:自然科学版,2013,29(2):1-5.
Some applications of Rota-Baxter operators
Zhou Shuyun
(Department of Computer Science and Engineering,Guangdong Peizheng College,Guangzhou 510830,China)
A Rota-Baxter operator is an abstraction and generalization of the integration operator.This paper studies the concept and basic properties of Rota-Baxter operators,and applications of Rota-Baxter operators on the ring of sequences with entries in some commutative rings,q-integral,matrix.
Rota-Baxter operators,k-algebras,commutative rings,matrix
O153.5
A
1008-5513(2017)05-0454-08
10.3969/j.issn.1008-5513.2017.05.002
2017-03-10.
广东培正学院重点资助项目(17pzxmzd1).
周淑云(1964-),硕士,教授,研究方向:Rota-Baxter代数及半群代数.
2010 MSC:18D50,17A30,17A50
