某类具有对称共轭点的倒星象函数的三阶Hankel行列式上界估计

张海燕, 马丽娜, 王焕

(赤峰学院数学与统计学院,内蒙古 赤峰 024000)

某类具有对称共轭点的倒星象函数的三阶Hankel行列式上界估计

张海燕, 马丽娜, 王焕

(赤峰学院数学与统计学院,内蒙古 赤峰 024000)

利用从属关系引入了一类关于对称共轭点的倒星象函数类 Ss∗,c(A,B),用Toeplitz行列式讨论了上述函数类的三阶Hankel行列式H3(1),得到了该行列式的上界估计.其结果改进并推广了一些已有结论.

倒星象函数;对称共轭点;三阶Hankel行列式;上界估计

1 引言

设S表示单位圆盘D={z∈C:|z|＜1}内单叶解析且具有如下形式的函数族:

设P表示单位圆盘D={z∈C:|z|＜1}内具有如下形式且满足条件Re p(z)＞0的函数族:

由文献[1]中的结论易知,对于函数p(z)∈P,存在Schwarz函数ω(z),使得

定义1.1[2]设函数f(z)和g(z)在单位圆盘D内解析.如果存在D内的Schwarz函数ω(z),满足:ω(0)=0,|ω(z)|＜ 1且 f(z)=g(ω(z)),则称 f(z)从属于 g(z),记为 f(z)≺ g(z).特别地,如果g(z)在D内单叶,则

设函数f(z)∈S,若满足

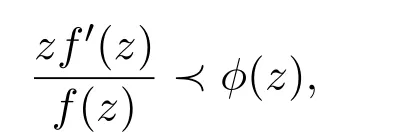
则称函数 f(z)属于函数类 S∗(ϕ),其中 ϕ(z)∈P.函数类 S∗(ϕ)和相应的凸函数类 K(ϕ)详见文献[3].

1959年,Sakaguchi在文献[4]中引入关于对称点的星象函数类S∗,f∈S∗当且仅当

1987年,El-Asha和 Thomas在文献 [5]中引入并分别研究了关于共轭点的星象函数类和关于对称共轭点的星象函数类,分别满足如下条件

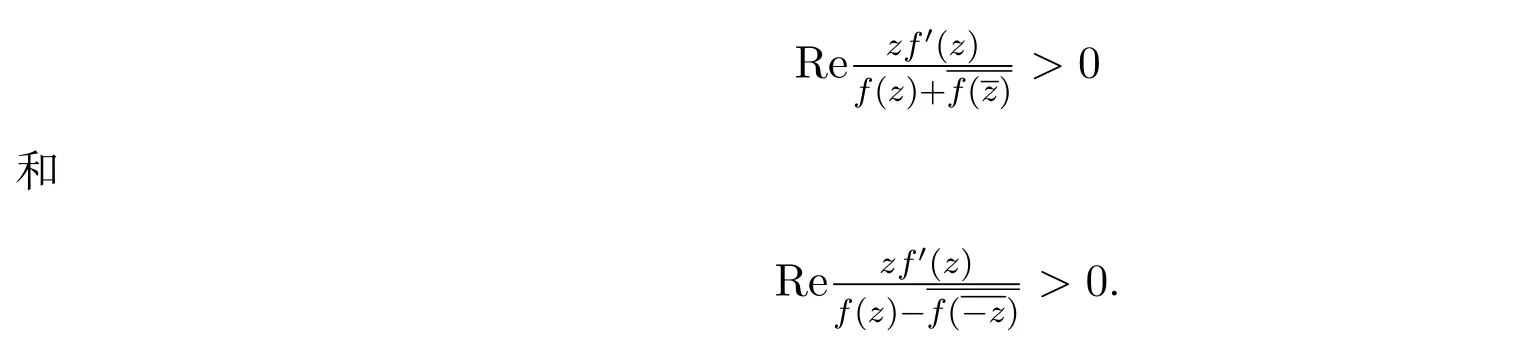
利用从属关系,本文引入了关于对称共轭点的倒星象函数类S∗sc(A,B)如下.

定义1.2设是具有(1)的形式且满足下面条件的函数全体,

其中−1≤B＜A≤1.

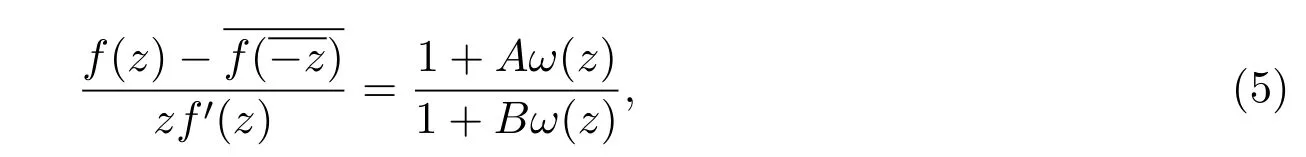
其中ω(z)是单叶解析函数,且满足

1976年,Noonan和Thomas[6]定义了函数f的q阶Hankel行列式:

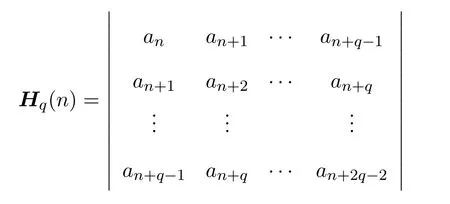
其中a1=1,n≥1,q≥1.

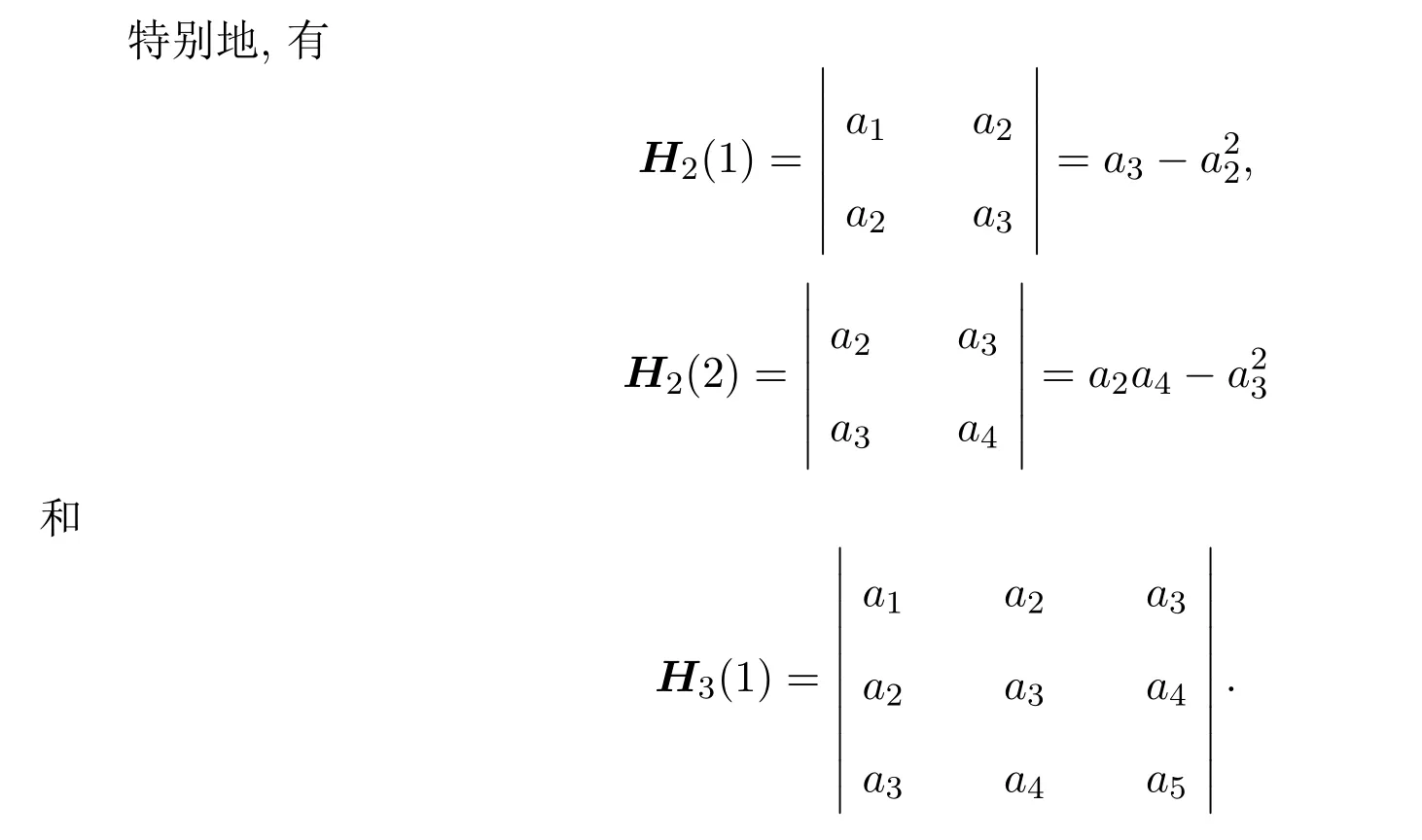
因为 f∈S,a1=1,故有

其中 H2(1)的上界估计即是经典的Fekete-Szeg不等式[7].

近年来,越来越多的学者对Hankel行列式的研究产生了浓厚的兴趣.Noonan和Thomas研究了p叶函数的二阶Hankel行列式[6],Noor在文献[8]中研究了星象函数的行列式Hq(n),并确定了当n→∞时,行列式Hq(n)的增长率.其他相关研究详见文献[9-11].受以上启发,张海燕、汤获等在文献[12]中研究了一类与对称点有关的一类解析函数Ms(α,µ,A,B)的三阶Hankel行列式H3(1),并得到了其上界估计.利用类似的方法,本文研究了与对称共轭点有关的一类倒星象函数S∗s,c(A,B)的三阶Hankel行列式H3(1),给出了该行列式的上界估计.

2 主要结果

除非特别说明,在本文中,我们总假设−1≤B＜A≤1.为了证明本文结论,需要如下引理.

引理 2.1[2]如果p(z)∈P,则引理 2.2[13]如果p(z)∈P,则存在复数x,z,满足 |x|≤1,|z|≤1,使得

定理 2.1设f∈,则

证明设,则由定义1.2和(5)式,可得

其中 ω(z)是 Schwarz函数且满足 ω(0)=0,|ω(z)|≤1,z∈D.令

则有

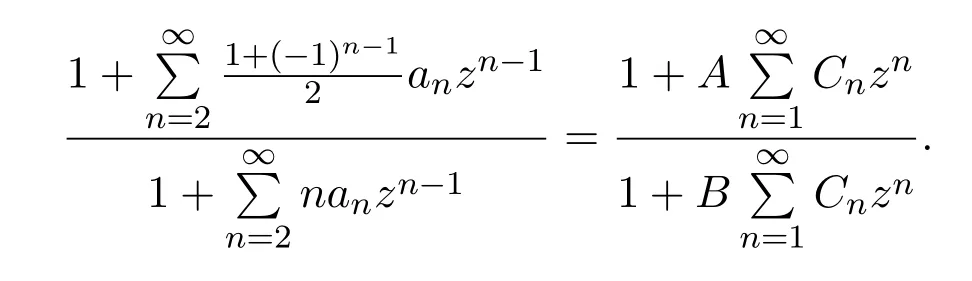
进而可得

分别比较上式中z,z2,z3,z4的系数,易得

定理2.1得证.

定理 2.2若,则有

证明设,由从属定义和(1.5)式可得

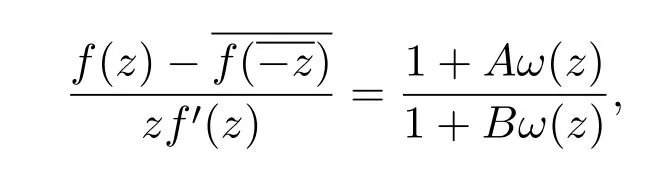
其中 ω(z)是单叶解析函数,且满足ω(0)=0,|ω(z)|≤1,z∈D.令

显然 p(z)∈P,且

因此有

分别比较(14)式中等号两边z,z2,z3的系数,得

于是,有

从而,有

设

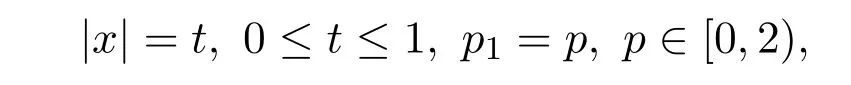
又因为|z|≤1,则由三角不等式和引理2.2,可得

进而,有

显然 p=0是 G(p)的根.又因为 G′′(0)＜ 0,所以 G(p)在 p=0处取到最大值.因此函数F(p,t)在t=1,p=0处取得最大值,即

定理2.2得证.

定理2.3若,则有

证明此定理的证明方法与定理2.2类似,在此省略其证明过程.

定理2.4若,则有

证明由(15),(16),(17)式,可得

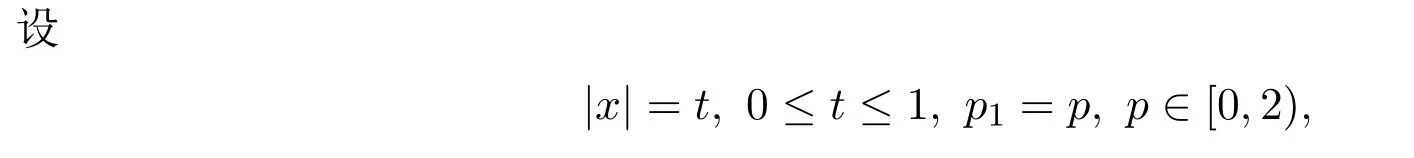
又因为|z|≤1,则由三角不等式和引理2.2,可得

下面分两种情况进行讨论:

(1)当 t ＞ t∗时,＜0,函数F(p,t)关于t严格单调递减,F(p,t)在t=0取最大值,即

显然 p=0是 G(p)的根.又因为 G′′(0)＜0,所以G(p)在 p=0处取到最大值.因此函数F(p,t)在t=0,p=0处取得最大值,即

(2)类似地,当t≤t∗时,≥0,函数F(p,t)关于t单调递增,F(p,t)在t=1处取得最大值,即

进而,有

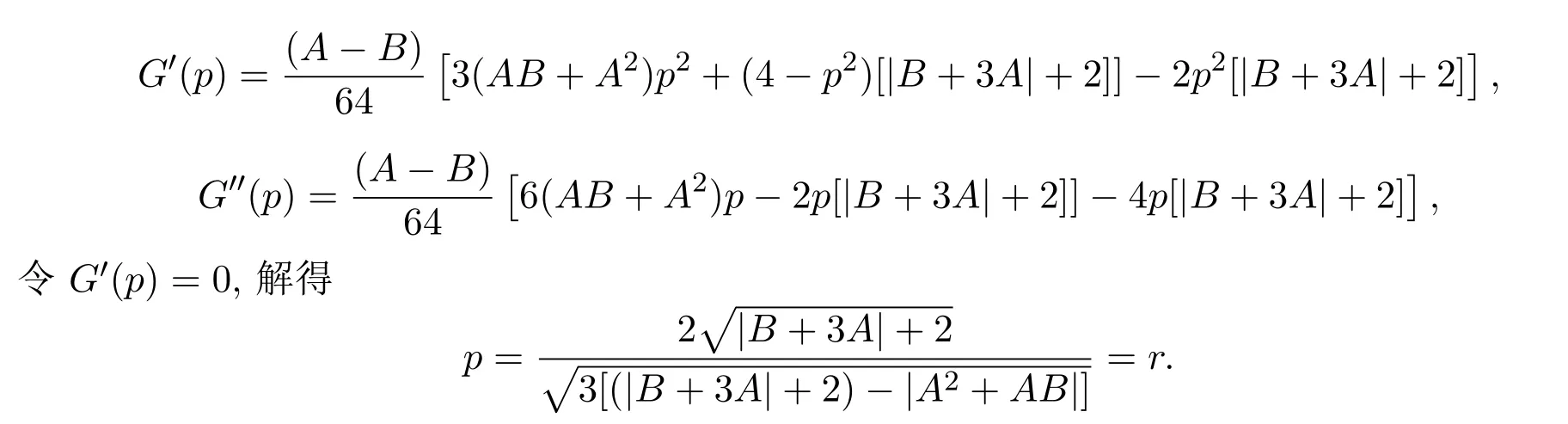
又因为G′′(r)＜0,所以G(p)在p=r处取到最大值.因此函数F(p,t)在t=1,p=r处取得最大值,即

综上可知,定理2.4得证.

定理 2.5设,则有

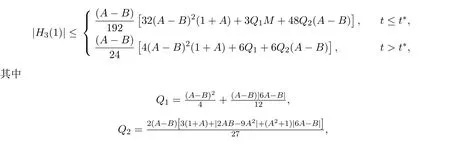
t∗,M,r分别由 (20),(21),(22)式给出.

证明因为

故由三角不等式可得

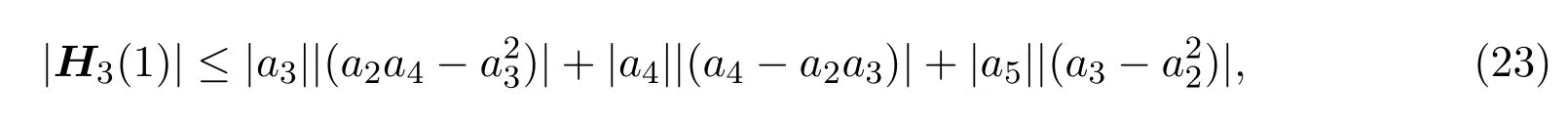
将(10),(11),(12),(13),(18),(19)式代入到(23)式,即得定理2.5的结论.

[1]Graham I,Kohr G.Geometric Function Theory in One and Higher Dimensions[M].New York:Marcel Dekker,Inc.,2003.

[2]Duren P L.Univalent Functions[M].New York:Springer Verlag,1983.

[3]Sakaguchi K.On a certain univalent mapping[J].J.Math.Soc.Japan,1959,11:72-75.

[4]El-Ashah R M,Thomas D K.Some subclasses of close-to-convex functions[J].J.Ramanujan Math.Soc.,1987,74(4):85-100.

[5]Halim S A.Functions starlike with respect to other points[J].Intermat J.Math.Math.Sci.,1991,14(3):451-456.

[6]Noonan J W,Thomas D K.On the second Hankel determinant of areally mean p-valent functions[J].Transactions of the American Mathematical Society,1976,223(2):337-346.

[7] Fekete M,SzegG.Eine benberkung uber ungerada schlichte funktionen[J].J.London Math.Soc.,1933,8(2):85-89.

[8]Noor K I.Hankel determinant problem for the class of functions with bounded boundary rotation[J].Rev.Roumaine Math.Pures Appl.,1983,28(8):731-739.

[9]Singh G.Hankel determinant for new subclasses of analytic functions with respect to symmetric points[J].Int.J.of Modern Mathematical Sciences,2013,5(2):67-76.

[10]Raza M,Malik S N.Upper bound of the third Hankel determinant for a class of analytic functions related with lemniscate of bernoulli[J].Journal of Inequalities and Applications,2013,2013(1):1-8.

[11]Sudharsan T V,Vijayalakshmi S P.Adolf Stephen B.Third Hankel determinant for a subclass of analytic univalent functions[J].Malaya J.Mat.,2014,2(4):438-444.

[12]张海燕,汤获,马丽娜.一类解析函数的三阶 Hankel行列式上界估计[J].纯粹数学与应用数学,2017,33(2):211-220.

[13]Libera R J,Zlotkiewicz E J.Coefficients bounds for the inverse of a function with derivative in positive coefficients[J].Proc.Amer.Math.Soc.,1983,87(2):251-257.

The estimate of upper bound of third Hankel determinant for a class of reciprocal starlike functions with respect to symmetric conjugate points

Zhang Haiyan,Ma Lina,Wang Huan
(School of Mathematics and Statistics,Chifeng University,Chifeng 024000,China)

In this paper,we introduce a class of reciprocal starlike functions with respect to symmetric conjugate points use affiliation,denoted by.we investigate the Hankel determinant H3(1)for this class functions with Toeplitz determinant and obtain the estimate of upper bound of the above determinant.The results present here improve and generalize some known results.

reciprocal starlike functions,symmetric conjugate points,third Hankel determinant,upper bound

30C45,30C50

A

1008-5513(2017)05-0503-10

10.3969/j.issn.1008-5513.2017.05.008

2017-07-07.

国家自然科学基金(11561001;11761006);内蒙古自治区高等学校科学研究项目(NJZY16251).

张海燕(1981-),硕士,讲师,研究方向：算子代数与复分析.

2010 MSC:30C45,30C55