一种基于主状态变量分离的降维仿真算法设计

张恒浩，唐庆博，唐 超，魏 明，刘丙利



一种基于主状态变量分离的降维仿真算法设计

张恒浩，唐庆博，唐 超，魏 明，刘丙利

（中国运载火箭技术研究院研究发展中心，北京，100076）

针对异步信息融合算法中状态向量维数过多和推导出来的协方差维数过高而导致的计算量增大的问题，提出一种基于主状态变量分离的降维仿真算法，将组合导航系统中进行计算的状态变量进行分类，确定主变量和次变量，在保证系统精度要求的前提下减小系统的计算量，从而保证系统的实时性工作要求。仿真结果证明该算法在满足系统精度要求的前提下能够有效减少系统的计算量，满足系统的工程实时性要求。

变量分离；主变量；次变量；降维；组合导航

0 引 言

在组合导航系统工作过程中，为解决由于导航传感器增多而引起的组合导航异步融合问题，在组合导航系统工作过程中引入了异步融合处理算法。虽然异步融合处理算法能够较好地解决组合导航系统中出现的异步计算问题。但随着导航方法的增多，导航子系统提供的数据不断增加，势必导致组合导航系统状态方程的维数越来越大。因此在异步融合处理计算过程中求解出来的协方差矩阵的维数相当高，导致一般的异步融合处理算法计算量大且复杂度高，在实际工程工作中不能很好地保持实时性。

本文以惯性导航系统和GPS卫星定位系统组成的组合导航系统为研究对象，将组合导航系统中状态方程提供的状态误差量进行分类，从中提取出主变量；然后通过组合导航算法中的特点再对主变量组成的状态方程进行降维计算的设计。在保证系统性能要求的前提下减小系统的计算量，从而达到简化融合算法、满足工程实时性工作要求的目的。

1 组合导航系统状态变量分析

从理想状态分析，为能够完整全面地描述飞行器的系统状态的性能，飞行器组合导航系统需要有24个误差状态变量来描述飞行器的工作状态，具体的误差状态量的表达式如下[1]：

从式（1）中可以看出，在飞行器组合导航方程组的误差状态描述中，当飞行器的型号、基本技术指标确定后，这24个状态变量中有一部分可以简化成常量。因此在计算过程中可以将这些状态变量从状态方程中分离，将这些变量设置为常数[2~5]，从而在不影响飞行器导航计算精度的前提下简化计算量。

位置误差、速度误差和姿态角误差需要在状态方程计算中进行变量计算。另外的一些变量如陀螺的刻度误差变量和安装角误差角，在计算过程中可以认为是常量。在组合导航系统的状态计算中可以分离出来。这样就减小了状态方程维数，有利于降低系统计算量，实现系统工程工作的实时性。

综上分析，在组合导航系统中，可以将组合导航系统涉及到的变量分为两类：主变量，包括位置、速度和加速度的误差状态变量；次变量，主要包括安装角误差、刻度误差等误差状态变量[6~8]。

本文在设计异步融合降维算法的过程中，可以将次变量从组合导航系统的状态方程中删去，将次变量看作常数进行解算。这样可以降低组合导航系统状态方程的维数，有利于降低整体计算量，保证导航解算工作的实时性要求。

2 基于主状态变量分离的降维算法设计

根据组合导航系统提供的导航量测信息，式（2）中的误差状态变量包括位置误差变量、速度误差变量和姿态角误差变量。这些误差状态变量统称为主变量，主变量可以按下面方法分为两组：

a）由于组合导航系统中的位置误差状态变量和速度误差状态变量由GPS系统提供修正信息进行修正，因此将位置误差和速度误差状态变量设为第1组主变量；

b）姿态角误差状态变量仅由惯性导航系统在工作过程中误差漂移和积累产生，因此将姿态角误差状态变量设为第2组主变量。

组合导航系统的状态方程式如下：

=。

因此，式（3）可以分解成如下两个状态方程：

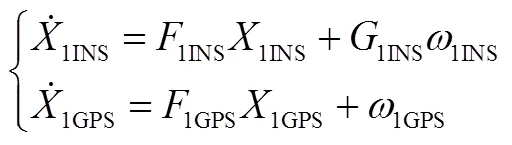
（5）

所以组合导航系统的量测方程也需要分解为如下两个量测方程：

（7）

从状态主变量分离过程中可看出，式（4）和式（6）可组成第1组状态主变量的组合导航系统的状态方程组，这组状态误差量可以通过GPS系统提供量测信息来修正惯性导航系统工作时引起的误差。而式（5）和式（7）可组成第2组状态主变量的组合导航系统的状态方程组，这组状态方程组由惯性导航系统系统单独工作解算。

因为GPS定位系统没有提供相对于姿态角误差变量的修正信息，所以状态主变量中的姿态角误差是通过惯性导航系统单独求解得到的。

式（4）~（7）的计算过程说明将飞行器导航系统主变量状态方程和量测方程分解后，GPS系统对其中的一部分状态变量做误差修正来保证系统的导航精度，其余变量由惯性导航系统解算求出。

这种分解降维算法在保持组合导航系统性能要求的前提下会大幅度减少系统状态方程的计算量，满足组合导航系统的实时性计算要求[9]。

综上所述，基于主状态变量分离的降维仿真算法计算步骤如下：

a）将飞行器组合导航系统中描述的状态变量分为主变量和次变量；

b）将次变量分离出系统状态方程；

c）根据组合导航的量测方程将主状态变量分成两个子状态变量集合和，其中子状态变量集合中的变量由组合导航量测方程中所包含的变量构成，子状态变量集合中的变量由只有在惯性导航系统状态变量中单独包含的变量构成；

d）根据两个分离的子状态变量集合分别设计状态方程和量测方程，然后对飞行器进行导航定位解算；

e）返回步骤c），进行循环计算。

图1表示的是基于主状态变量分离的组合导航系统降维设计的算法流程。

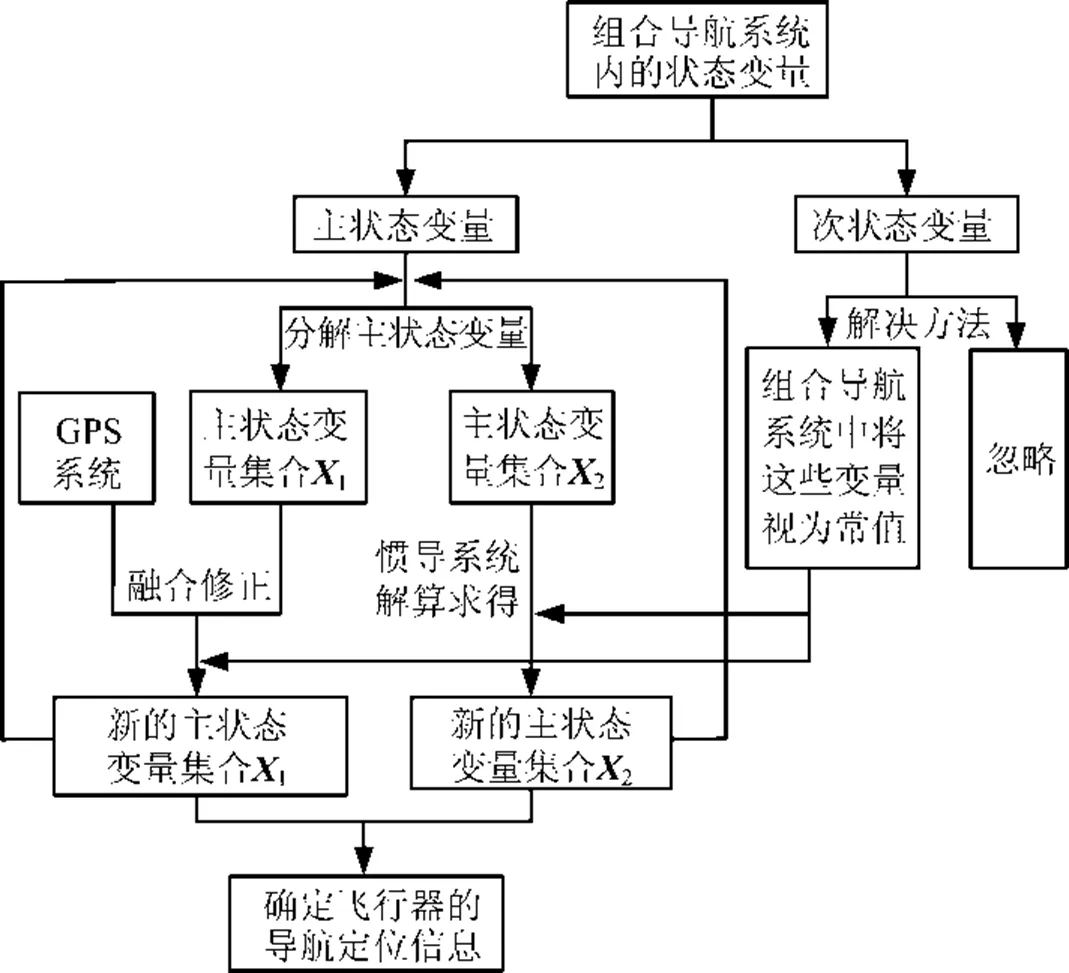
图1 基于主状态变量分离的组合导航系统降维设计算法流程

3 仿真验证

飞行器组合导航系统仿真算例的参数设计如下[10]：

飞行器的速度初始误差、姿态角初始误差和初始位置误差的数值均为零；初始速度为正东方向300 m/s，初始位置为北纬30°、东经120°，初始高度为5 000 m，仿真时间为300 s。

根据系统任务对飞行器的要求，飞行器在飞行300 s之后可以允许的误差范围如表1所示。

表1 状态变量允许误差范围

根据任务要求，300 s后导航系统提供的指令延迟时间应控制在0.01 s内。

设GPS卫星导航定位系统提供的导航状态为位置和速度的误差状态量，表达式如下：

因为惯性导航系统量测方程中包含的量测量也有位置误差和速度误差状态量，所以组合导航系统中所包含的9个主状态误差变量可以根据GPS卫星定位系统提供的量测方程信息分为两组状态变量。

（10）

根据上述分析方法，将式（3）分解成如下两个状态方程：

（12）

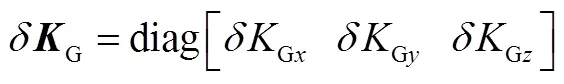
（14）

同样方法对组合导航系统量测方程进行降维分解，量测方程可以分解如下：

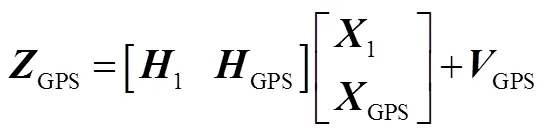
（16）

在组合导航系统中引入基于主状态变量分解降维算法，组合导航系统的状态方程和量测方程可以分解为两组方程；这样在计算过程中减小了计算量，有利于组合导航系统在保证精度的前提下满足工程计算的实时性要求。

根据信息融合算法在工程上应用经验来看，融合计算的计算量与状态方程的维数的3次方近似成正比。

从式（17）、式（18）的计算结果可知，基于主状态变量的降维设计算法和原来采用主变量整体计算的方法相比，其计算量大概是主变量整体计算方法的三分之一。基于主状态变量的降维设计算法和原来的全面表示载体导航运动信息的24维状态方程算法相比，其计算量约是24维整体融合算法的0.017 6倍。

（18）

根据上述推导结果做仿真计算，图2~ 4表示的是分离出来的姿态角变量在惯性导航系统下单独作用计算时的误差情况。

图2 降维融合算法俯仰角误差

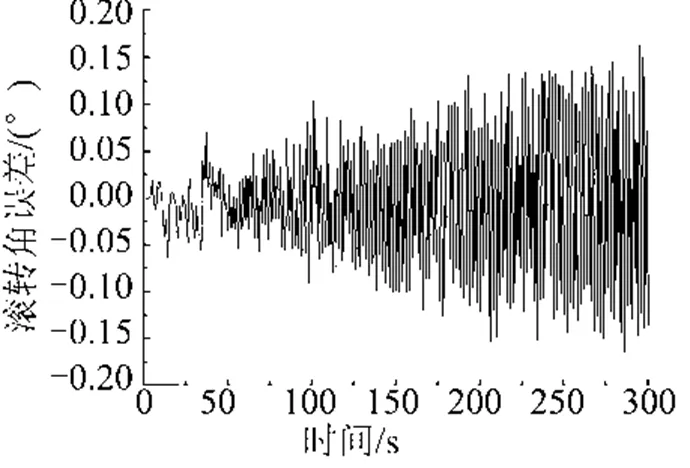
图3 降维融合算法滚转角误差

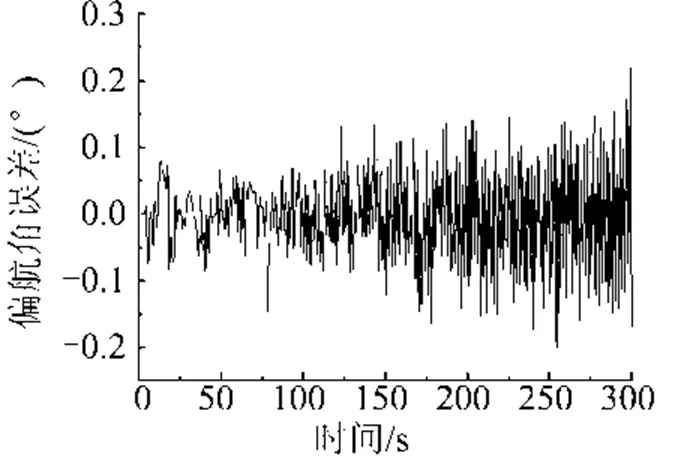
图4 降维融合算法偏航角误差

图5~ 9表示的是基于主状态变量降维融合算法得到的位置误差和速度误差与原来融合算法得到的位置误差与速度误差的比较情况。

图5 东向速度误差结果比较

图6 北向速度误差结果比较

图7 天向速度误差结果比较

图8 北向位置误差结果比较

图9 东向位置误差结果比较

采用传统导航24维状态变量融合算法得到的仿真计算误差范围及误差比例范围如表2所示；采用本文提出的主状态变量分析法得到的仿真计算误差范围及误差比例范围如表3所示。误差比例范围在(-1, 1)之间说明系统误差在允许范围内。误差比例范围两端的极值越接近0，表明状态变量在工作过程中的精度越高。

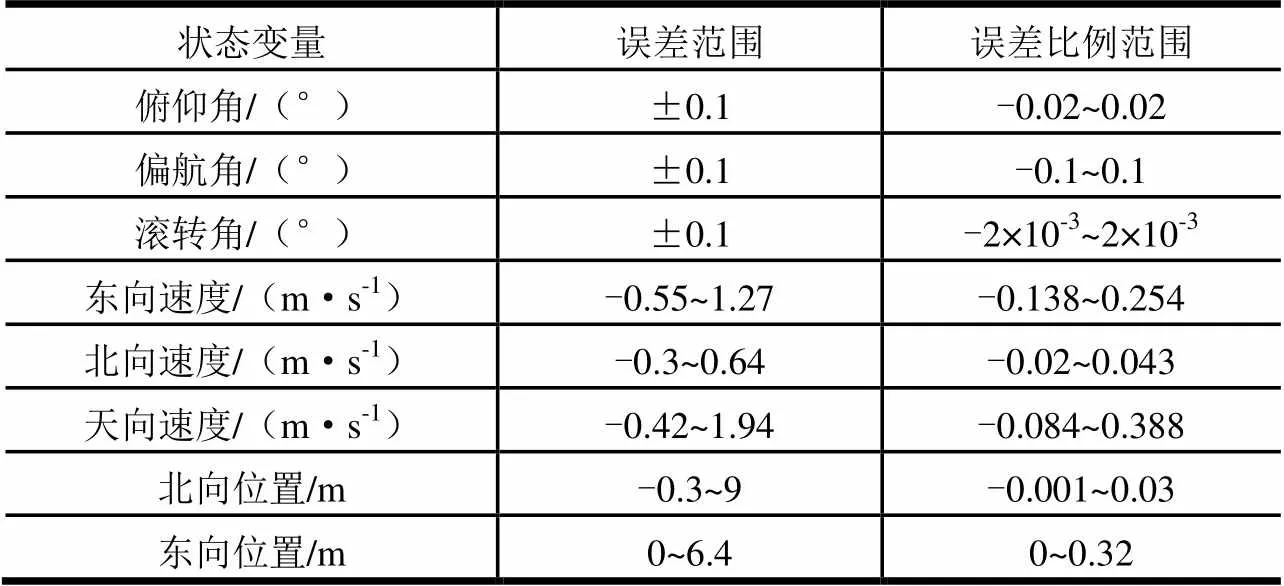
表2 24维状态变量计算误差范围及比例计算

表3 主状态变量分离算法误差范围及比例计算

仿真计时器对两种方法的计算延时时间分析，当采用导航24维状态变量融合算法时，运行到300 s时系统计算指令的延时时间为0.010 7 s；采用主状态变量分离的降维算法时，运行到300 s时系统计算指令的延时时间为1.9×10-4s。可见采用改进后的主状态变量分离的降维算法能够满足系统的实时性要求；传统的全维状态变量融合算法由于状态变量多，计算量大，当系统运行到300 s时，由算法计算而产生的延时时间已经不能满足系统实时性要求。

从表2和表3的仿真结果看出，采用主状态变量分离的算法得到的计算精度虽不如传统完整的导航算法精度高，但是在系统任务允许的误差范围内仍有较好的精度。且分解降维后的算法在运行时计算指令的延时时间大幅度降低，满足了系统任务的实时性要求。

4 结 论

针对异步融合算法中状态变量过多引起的计算量大的问题，提出一种基于主状态变量分离的降维设计方法。利用组合导航系统量测方程给出的主状态变量范围，将整个系统的主状态变量进行分离降维设计。在保证系统工作精度下采用这一方法可以大幅度减小系统的计算量，从而满足系统的工程实时性指标要求。

[1] 龚文飞，孙昕. 多级嵌套维纳自适应降维STAP抗干扰方法研究[J]. 宇航学报, 2010, 10, 31(10): 2360-2366.

[2] Grewal M S. Global positioning systems, inertial navigation, and integration[M]. Houston: A John Wiley & Sons, Inc. Publication, 2001.

[3] 董金良, 王荫槐, 王峰. 基于改进加权航迹关联的异步融合算法与仿真[J]. 电子技术应用, 2010(1): 99-102.

[4] 王晓旭, 赵琳, 潘泉. 基于最小均方差估计的噪声相关UKF设计[J]. 控制与决策, 2010, 25(9): 1393-1398.

[5] 盛蔚, 谭丽伟. MGNC系统实时快速组合导航新算法[J]. 北京航空航天大学学报, 2009, 35(6): 657-660.

[6] Wendel J. Comparison of extended and sigma - point Kalman filters for tightly coup led GPS/INS integration[C]. Houston: AIAA Guidance, Navigation and Control Conference, 2005: 2005-2055.

[7] Shalom B. Update with out-of sequence measurements in tracking: exact solution[C]. Bellingham: Proceeding of 2000 SPIE Conference on Signal and Data Processing of Small Targets, 2000.

[8] 马卫华, 罗建军. 空间转移飞行器自主导航系统SINS/GPS/SS的卡尔曼滤波器降阶方案[J]. 宇航学报, 2008, 29(5): 1556-1562.

[9] 朱芳来, 韩正之. 基于Riccati方程解的非线性降维观测器[J]. 控制与决策, 2002, 17(4): 427-430.

[10] 曹向海, 刘宏伟. 基于奇异值分解的双谱降维研究[J]. 宇航学报, 2007, 28(5): 1319-1322.

The Reduction of Dimensions Simulation Algorithm Based on the Main State Separating

Zhang Heng-hao, Tang Qing-bo, Tang Chao, Wei Ming, Liu Bing-li

(R&D Center, China Academy of Launch Vehicle Technology, Beijing, 100076)

In order to solve the problem that the calculated quantity increases due to increasing of the state variables, a depressed dimension simulation algorithm based on the main state variables separating was put forward. First of all, classified the state variables calculated in the integrated navigation system. Secondly, confirmed the main variables and the secondary variables. Finally, decreased the workload of the whole navigation system equations on the premise that the system precision was guaranteed, the real-time working requirements of the system can be guaranteed. The simulation result showed that this algorithm can reduce the integrated navigation system’s workload when the precision requirements of the system can be satisfied and the algorithm can meet the engineering real-time working requirements of the system.

Variables separating; Main variables; Secondary variables; Descend dimension; Integrated navigation system

1004-7182(2016)02-0061-05

10.7654/j.issn.1004-7182.20160214

V448

A

2015-08-26；修改日期：2015-11-12

张恒浩（1982-），男，博士，工程师，主要研究方向为飞行器导航、制导与控制