复合高斯杂波中子空间信号的自适应检测

张洋忠，张 玉，唐 波

(解放学电子工程学院，安徽 合肥 230037)

复合高斯杂波中子空间信号的自适应检测

张洋忠，张 玉，唐 波

(解放学电子工程学院，安徽 合肥 230037)

针对复合高斯杂波中自适应检测多维子空间信号，传统算法在训练样本数有限的情况下性能严重不足的问题，提出了基于协方差矩阵广对称结构信息的子空间信号的广对称自适应检测算法。该算法利用协方差矩阵的广对称结构特征，基于两步广义似然比准则，首先得到协方差矩阵的广对称渐进最大似然估计，然后代入似然比得到广对称自适应检测器,理论分析证明了该检测器具有恒虚警率特性。仿真分析表明,与传统检测器相比，该检测器具有更好的检测性能。

自适应检测；子空间信号；复合高斯杂波；广对称结构；广义似然比准则；恒虚警率

0 引言

杂波和目标模型的建立以及检测器设计是雷达目标检测的两大类基本问题[1]。自适应检测目标的核心问题之一是准确估计杂波协方差矩阵。工程实际中通常选择待检测单元邻近的参考单元数据作为训练样本来估计其杂波协方差矩阵。为了得到杂波协方差矩阵的有效估计，要求训练样本与待检测单元快拍矢量独立同分布。根据Reed-Mallet-Brennan(RMB)准则[2]，当独立同分布训练样本数不低于系统维数的两倍时，自适应检测性能才能够得到有效保证。

在实际环境中，地形变换、杂波起伏和目标干扰等因素都会导致杂波不均匀[3]，进而导致得到的训练样本与待检测单元快拍矢量不再独立同分布。如果使用这些非均匀训练样本来估计杂波协方差矩阵，自适应检测性能将可能急剧下降。因而，在非均匀杂波环境中可用于有效估计杂波协方差矩阵的训练样本数将极为有限。

在复合高斯杂波中自适应检测子空间信号时，文献[4]和[5]分别针对点目标和距离扩展目标推导得到了基于广义似然比准则(Generalized Likelihood Ratio Test, GLRT)的检测器。这些传统检测算法在训练样本数有限的情况下存在性能严重不足的问题。针对此问题，提出了复合高斯杂波中子空间信号的广对称自适应检测算法。

1 信号模型和传统GLRT检测器

1.1 信号模型

假设均匀线性阵列具有Na个阵元，每个阵元在相干处理间隔内发射Nc个相干脉冲，那么单个距离单元内N=NaNc。那么复合高斯杂波中信号检测问题可以表示为如下二元检测问题：

(1)

其中，z∈N×1表示检测单元观测数据，x∈N×1表示目标信号，c∈N×1表示检测单元杂波数据。

将杂波建模为复合高斯模型，杂波c可以表示为一个非负随机变量τ(称为文理分量)和一个均值为零、协方差矩阵为M的复随机矢量g(称为散斑分量)，即

(2)

如果均匀线性阵列关于相位中心对称分布或者脉冲串间隔对称，那么杂波协方差矩阵具有埃尔米特(Hermitian)结构和广对称(Persymmetric)结构[6]。

假定协方差矩阵M具有埃尔米特结构和广对称结构双重对称结构特性，即M满足

M=MH和M=JM*J

(3)

其中，(·)*表示复共轭，J表示副对角线为1其余位置为0的置换矩阵。

将目标信号建模为多维子空间模型[5]，即

x=Ea

(4)

其中，E∈CN×r表示目标导向矩阵并且秩为r，a∈Cr×1表示目标散射体的幅度矢量。在工程实际中，E可以用观测数据估计得到。本文中假定a是未知的确定性矢量。

导向矩阵E可以表示为：

(5)

假定目标运动足够缓慢或者观测时间足够短，那么相位线性变化，即

(6)

为使导向矩阵具有广对称结构，在保持目标信号特征参数不变的条件下，对E的列矢量进行等价变换。当N为奇数时，E变换为：

(7)

当N为偶数时，E变换为

(8)

该变换是将该导向矩阵变成以相干脉冲串的中心作为起始时刻的导向矩阵形式，变换前后导向矩阵的目标特征参数信息不变，因而该变换是一一对应的。从式(7)、(8)显然可以看出，变换后的矩阵E具有广对称结构，即E=JE*。

1.2 传统GLRT检测器

传统GLRT检测器不利用协方差矩阵的广对称结构信息，文献[4]中给出了传统GLRT检检测器的检验统计量为：

(9)

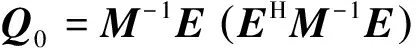
2 广对称自适应检测算法

定理[7]：定义T为如下酉矩阵：

(10)

其中，I表示单位矩阵。广对称导向矩阵E和双重对称协方差矩阵M有如下性质：

1)E是广对称矩阵当且仅当TE是一个实矩阵；

2)M是广对称矩阵当且仅当TMTH是一个实对称矩阵。

利用该定理，式(1)中原始二元检测问题可以重新表示为

(11)

2.1 广对称自适应检测器

针对式(11)中二元检测问题，应用两步GLRT方法。第一步，假设协方差矩阵MP已知，得到检验统计量；第二步，利用K个训练样本得到协方差矩阵MP的估计值，然后代入到检验统计量中。

i=0,1

(12)

那么，检验统计量为：

(13)

其中，γ是检验门限。并且a的最大似然(Maximum Likelihood, ML)估计值为：

(14)

τ在假设Hi，i=0,1下的ML估计值分别为：

(15)

(16)

因此检验统计量可以写为：

(17)

第二步，利用K个训练样本z1,…,zK估计协方差矩阵MP。协方差矩阵M的渐进最大似然(Asymptotic ML, AML)估计[8]为：

(18)

迭代次数取L=4[8]，初始化值取协方差矩阵M的正则化样本协方差矩阵

(19)

因此协方差矩阵MP的渐进最大似然估计为：

(20)

2.2 广对称自适应检测算法

(21)

那么Λ的概率密度函数为：

(22)

因此，虚警率为：

(23)

式(23)中，虚警率表达式与纹理参量τ和散斑分量协方差矩阵M均无关，所以该检测器PGLRT对纹理分量和散斑分量协方差矩阵具有恒虚警率特性。

3 仿真与性能分析

本小节采用蒙特卡洛仿真法对子空间信号的广对称自适应检测器PGLRT进行性能分析，并与未考虑协方差矩阵的广对称性质的传统检测器进行性能比较。并从协方差矩阵估计方法、信号子空间维数和信号子空间失配三个方面对PGLRT检测器性能影响进行分析。蒙特卡洛仿真次数为100/Pfa，为了减少计算负担，本小节选取虚警率Pfa=10-2。观测数据矢量维数N=8。

(24)

假定杂波散斑分量协方差矩阵是指数结构矩阵，其元素值为：

(25)

其中，ρ为一步滞后相关系数，本文取ρ=0.9。

定义信杂比为：

(26)

其中，σ2表示杂波功率。

3.1 与传统检测器性能对比

图1给出了训练样本数K分别为8、16、64时PGLRT和传统GLRT检测器的检测性能随信杂比的变化曲线图。由图可知，当训练样本数较少时，PGLRT检测性能明显优于传统GLRT；随着训练样本数增多，PGLRT改善检测性能减小；当训练样本数充足时，PGLRT对检测性能的改善作用很小。这是因为PGLRT利用了协方差矩阵的广对称结构信息，减少了对训练样本数的需求。

3.2 协方差矩阵估计方法的影响

本文给出了不考虑协方差矩阵广对称结构的渐进最大似然估计的AML估计方法和考虑广对称结构信息的PAML估计方法，分别如式(18)、(20)所示。图2给出了这两种协方差矩阵估计方法对检测器性能影响的分析图。从图中可以看出，在训练样本数不足时，PAML方法因为利用了广对称结构信息，因而对检测器性能有很大的改善；随着样本数的提高，改善程度将减小。

3.3 信号子空间维数的影响

由于工程实际中，信号子空间维数是由实测数据估计出来的，因而会有出现误差的可能，因此有必要分析信号子空间维数对检测器性能的影响。图3给出了信号子空间维数r分别为1、2、3时检测器性能曲线。可以看出，随着信号子空间维数的增大，PGLRT检测器性能降低。原因是，当信号子空间维数增加时，信号的不确定度也增大，并且信号子空间与杂波子空间更加接近从而造成信号能量的泄露，因此相同信杂比条件下，信号子空间维数越大，检测难度越大，检测概率越小。

3.4 信号子空间失配的影响

在工程实际中，目标信号所在距离单元的距多普勒频率是根据实测数据估计出来的，因而肯定会有多普勒频率估计误差存在，所以研究信号子空间多普率频率的失配对检测性能的影响是很有意义的。考虑信号子空间维数r=2，匹配多普勒频率fd=[0.1,0.2]的情况。图4给出了信号子空间匹配和失配时检测器性能曲线。由图可以看出，信号子空间失配越严重，检测性能下降越大，当失配程度较小时，检测性能几乎没有影响。说明PGLRT对信号子空间失配就有一定的稳健性，可以容忍较小程度的信号子空间失配。

4 结论

本文提出了复合高斯杂波中多维子空间信号的广对称自适应检测算法。该算法利用协方差矩阵的广对称结构特性，对检测问题做了一个等价变换，然后采用两步GLRT准则，其中协方差矩阵采用广对称渐进最大似然估计，得到子空间信号的广对称自适应检测器PGLRT。理论分析证明了PGLRT对纹理分量和协方差矩阵具有恒虚警率特性。仿真验证表明PGLRT检测器比传统不利用广对称结构信息的GLRT检测器性能更好。同时证明了PGLRT检测器在估计协方差矩阵时利用广对称结构信息能够提高检测性能，随信号子空间维数的增大而性能下降，并且对信号子空间失配具有一定的鲁棒性。

[1]唐波, 汤俊, 彭应宁. 圆台阵列杂波模型及空时二维自适应处理[J]. 航空学报, 2010, 31(3): 587-592.

[2]REED I S, MALLETT J D, Brennan L E. Rapid convergence rate in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1974 (6): 853-863.

[3]JAVIER C M, JAVIER G M,LVARO B D C, et al. Statistical analysis of a high-resolution sea-clutter database[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(4): 2024-2037.

[4]GINI F, FARINA A. Vector subspace detection in compound-Gaussian clutter. Part I: survey and new results[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(4): 1295-1311.

[5]BON N, KHENCHA A, GARELLO F. GLRT subspace detection for range and Doppler distributed targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2008, 44(2): 678-696.

[6]NITZBERG R. Application of maximum likelihood estimation of persymmetric covariance matrices to adaptive processing[J]. IEEE Transactions on Aerospace and Electronic Systems, 1980 (1): 124-127.

[7]VAN TREES H L. Detection, estimation and modulation theory, part IV: optimum array processing[M]. Hoboken, NJ, USA: Wiley, 2002.

[8]GINI F, GRECO M. Covariance matrix estimation for CFAR detection in correlated heavy tailed clutter[J]. Signal Processing, 2002, 82(12): 1847-1859.

Subspace Signals Adaptive Detector in Compound-Gaussian Clutter

ZHANG Yangzhong, ZHANG Yu, TANG Bo

(Electronic Engineering Institute of PLA, Hefei 230037, China)

When detecting the multidimensional subspace signals in compound clutter, the traditional detectors’ performance is poor in the limitation on the number of training data. Aiming at this problem, a persymmetric adaptive detector was proposed by exploiting the persymmetric structure of the covariance matrix. This detector first obtained the Persymmetric asymptomatic maximum likelihood estimater of the covariance matrix and then substituted it to the test statistic which was obtained by the generalized likelihood ratio test approach. The detector was shown to possess the constant false alarm rate property. Simulations indicated the detector’ performance improvement compared with the existing detectors. In addition, it could assess the detection performance with respect to the effects of the covariance matrix, signal subspace dimension and mismatched performance of signal subspace.

adaptive detection; subspace signals; compound-Gaussian clutter; persymmetric structure; generalized likelihood ratio test; constant false alarm rate

2016-09-17

国家自然科学基金项目资助(61201379)；安徽省自然科学基金项目资助(1608085MF123)

张洋忠(1992—)，男，江西鹰潭人，硕士研究生，研究方向：雷达信号处理，自适应目标检测。E-mail：zhangyz10@126.com。

TN957.51

A

1008-1194(2017)01-0096-05