螺距对引信内腔封口螺纹连接强度的影响

殷 瑱， 闻 泉， 王雨时， 张志彪

(南京理工大学机械工程学院，江苏 南京 210094)

螺距对引信内腔封口螺纹连接强度的影响

殷 瑱， 闻 泉， 王雨时， 张志彪

(南京理工大学机械工程学院，江苏 南京 210094)

针对引信内腔封口连接螺纹强度设计特别是螺距优选问题，对机械设计理论中螺纹应力的计算公式进行推导，提出了考虑到引信连接螺纹端头倒角、允许崩落长度和允许止量规适当进入等情形时引信内腔封口螺纹连接强度的计算方法。该方法在分析螺纹牙所受应力时仅需考虑与螺纹直径、螺距和连接长度相关的应力系数，使得计算过程简洁方便，计算结果准确可靠。结果表明：螺距对螺纹强度影响较为敏感，在不考虑螺纹制造误差和连接长度一定且有限的情况下，尽可能选用较小螺距有助于提高强度。螺纹强度校核时仅需考虑弯曲强度和剪切强度而不必校核挤压强度。就螺纹牙所受应力而言，螺纹牙所受剪切应力接近弯曲应力的一半。由于传统引信螺纹零件强度校核时未考虑弯曲强度，也未考虑螺纹牙受力不均、引信通用制造规范允许有螺纹牙崩落和止量规适当旋入等情形，致使螺纹连接强度计算结果过于冒进。

引信；螺纹；螺距；应力分析；连接强度

0 引言

螺纹作为零部件连接和紧固的主要方式，在产品设计中应用广泛。螺纹零件使用时由螺纹牙作为主要的承载部位，其承载能力直接关系到产品结构的稳定和可靠。在实际应用中，螺纹常因弯曲、挤压和剪切等作用出现失效。为解决螺纹连接失效的问题，曲萍[1]结合小口径阀体和阀盖的螺纹连接强度问题，利用螺纹强度计算公式和实例数据分析了影响螺纹强度的因素，发现螺距和螺纹误差对螺纹强度影响显著。段巍等[2]对大跨度建筑物中的钢拉杆螺纹连接强度问题进行了研究，通过理论分析、试验验证和有限元模拟的方法，确定了钢拉杆破裂载荷及正常连接所需的最小旋合扣数，计算了螺纹牙应力分布、应力状态以及各螺纹牙接触面间的压力和滑移变形规律。安晓卫等[3]应用有限元仿真软件分析得到了弹底与弹体连接螺纹的应力分布。倪庆杰等[4]对战斗部与火箭增程发动机壳体连接螺纹失效问题进行了研究。尽管理论分析和软件仿真在解决螺纹强度失效问题上均有应用，但是对于工程实践而言，理论分析和计算的方法应用更为普遍。

螺距是螺纹设计中的重要参数之一，但目前未见有人从理论上分析引信零件螺纹螺距对连接强度的影响。引信较大零、部件连接的主要方式是螺纹，引信内腔封口多由本体与传爆管之间的螺纹实现。在引信特别是在弹头隔爆型引信的发射、跌落和隔爆过程中，引信内腔封口连接螺纹(一般均为普通螺纹)要承受较大的、一次性的冲击过载。为保证引信工作的安全性和可靠性，螺纹零件必须满足发射(跌落)时的隔爆强度[5-6]，即要承受发射(跌落)时的惯性冲击与隔爆状态下的爆炸冲击的叠加。由于在总体设计时引信的整体尺寸已基本确定，所以事实上是限制了引信螺纹零件的连接长度。引信内腔封口连接螺纹在现代隔爆型引信中的强度设计，特别是在特M12×0.75、特M15×0.75、特M18×0.75等较小尺寸规格下，矛盾比较突出。在螺纹连接长度一定的情况下，增大螺纹螺距，单圈螺纹强度会增大，但工作圈数却减小了。因此，为了探讨螺距对引信内螺纹强度的影响，本文通过对机械设计理论中螺纹应力的计算公式进行推导，提出了考虑到引信连接螺纹端头倒角、允许崩落长度和允许止量规适当进入等情形时引信内腔封口螺纹连接强度的计算方法。

1 机械设计理论中的螺纹应力计算

内、外螺纹配合时，内螺纹应力要大于外螺纹应力。因此，以外螺纹为例来分析螺纹牙受力情况。将其单圈螺纹牙沿螺纹小径d1处展开后可看作是宽度为πd1的悬臂梁，如图1所示[7-8]。

假设每圈螺纹承受的平均压力为：

(1)

式(1)中，Q为螺纹承受的轴向载荷，N；z为螺纹连接圈数，z=l/P，其中l为已包括两端倒角部分的内、外螺纹有效连接长度，mm；P为螺距，mm。图1中b为螺纹牙底宽度，h为螺纹牙工作高度。

对于普通螺纹的基本牙型：d1=d-2h；H=0.866P；h=5H/8=0.541P；b=0.870P。

在轴向力Q的作用下，普通螺纹螺纹牙根部或表面受到的剪切应力τ、挤压应力σ和弯曲应力σw分别为：

(2)

(3)

(4)

式中，d为外螺纹大径，mm；M为螺纹牙底所受弯矩，N·mm；W为单圈外螺纹展开后的螺纹牙底截面的抗弯模量，mm3；kz为螺纹牙载荷不均系数，表示在不同圈数处螺纹牙受到轴向载荷作用的程度，常见内、外螺纹材料配对时螺纹牙的载荷不均系数如表1所列[7-8]。

表1 螺纹牙载荷不均系数[7-8]

由于P≪d，故由式(2)和(3)知，σ/τ≈1.848/1.149=1.608。已知[τ]≈0.25[σ][8],即[σ]≈4[τ]，故一般情况下，剪切应力比挤压应力危险，即只要剪切应力满足要求，挤压应力也会满足要求。

易证：恒有σw>σ且σw≈1.16σ。另已知[σw]≈0.5[σ][8]，故弯曲应力总是比挤压应力危险。

综上所述，普通螺纹强度只考虑剪切应力和弯曲应力即可。即只要剪切强度和弯曲强度满足要求，挤压强度即可满足要求。

由式(2)—式(4)可知，在l一定时，加大P则σw、σ和τ均加大。因此，在不考虑螺纹倒角、螺纹牙崩落、无效长度(允许止规适当进入所形成)和配合间隙影响的情况下，螺纹螺距越大，螺纹牙应力也越大，即对强度越不利。

文献[9]给出了MJ螺纹剪切应力工程计算公式：

(5)

式中，d2为螺纹中径，e为效率系数。对于钢，e=0.33。式(5)可进一步写成：

(6)

2 引信内腔封口连接螺纹应力分析

作为引信输出端的零件，传爆管壳通常以外螺纹与引信体内螺纹相连，实现引信内腔封口。该螺纹的连接强度直接影响引信发射(跌落)和隔爆时的安全性。文献[10]和[11]给出了引信传爆管壳外螺纹在轴向力Q作用下受到的剪切应力和挤压应力计算公式为：

(7)

(8)

式中，轴向力Q包括惯性力如后坐力和跌落冲击力，也包括隔爆状态下的压力。

文献[10]和[11]并未给出引信传爆管壳外螺纹的弯曲应力计算公式，也未指出要进行弯曲强度校核。与式(2)、式(3)和式(5)相比，式(7)和式(8)中分母上均少了小于1的螺纹牙载荷不均系数kz或效率系数e，且又以螺距P在剪切应力表达式分母上代替b=0.870P，事实上会使所得应力系统地偏小，即按此计算得到的引信螺纹强度结论将是过于冒进的，此时如果安全系数(裕度)设计不足，将会有强度失效的可能。

文献[5]及其有关参考文献、文献[12](俄文原版的出版时间是1944年)给出的引信内腔封口连接螺纹应力计算公式均与式(7)和式(8)相同。可见引信行业长期以来一直沿用前苏联的理论，未能考虑比挤压应力更危险的弯曲应力，并且基于刚体假设和形状、位置均正确假设，未能考虑螺纹牙载荷不均问题。

下面以式(2)—式(4)为基础分析引信内腔封口连接螺纹的强度问题。

一般来说，螺纹加工时螺纹始末两端应有倒角和收尾[13]。始端端面的倒角一般为45°，也可以采用60°或30°倒角；倒角深度应大于或等于螺纹牙型高度。从工艺角度分析，对于搓丝、滚压或扳牙加工的外螺纹，其始端因倒角所形成的不完整螺纹的轴向长度不会大于2P。但引信螺纹零件加工时一般为两端倒角，没有收尾。本文中假设倒角角度45°，倒角深度等于螺纹牙型高度h，则外螺纹两端不完整螺纹的轴向长度x1=2h=1.082P。

引信螺纹零、部件生产时，螺纹牙“丝尖”会因切削而产生崩落缺陷，其深度不应超出螺纹的中径(起闭气作用的螺纹，崩落深度应不大于螺纹高度的1/3)，崩落总长允许值如表2所列[14-15]。一般设计中，引信零、部件螺纹有效圈数都会大于2，故有效螺纹崩落总长有可能到2/3或1圈。考虑到内、外螺纹均有可能有允许的1圈之内的崩落，并且内、外螺纹各自崩落的部分未必会完全对应在一起，但崩落部分仍会有一定的连接强度，因此本文在计算螺纹强度时假设因崩落会有1圈即一个螺距的长度连接强度失效(不起作用)。

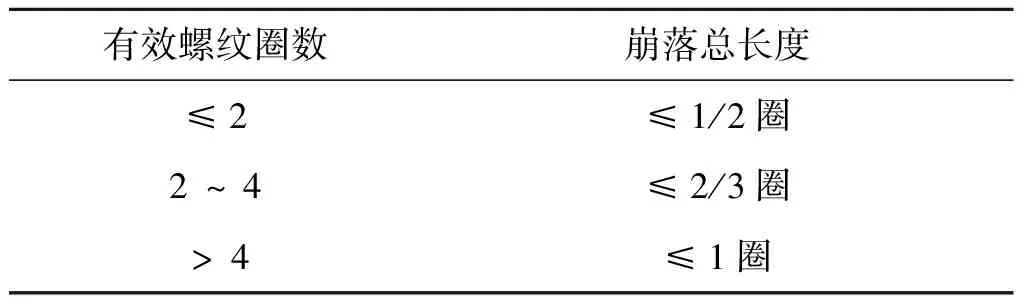
表2 引信允许有效螺纹崩落总长[14-15]

据文献[14]和[15]，引信螺纹零件在检验时，“止”螺纹量规不应旋入，或者能够旋入但旋入量不大于四扣且不大于螺纹长度的50%。用止光滑量规检验内螺纹小径时，允许进入螺纹总长的1/3。而在用止光滑量规检验外螺纹大径时，允许螺纹两端的大径局部缩小，其缩小量为大径公差的1/2。但每端缩小长不应大于螺纹总长的1/3，而两端缩小部分总长不得大于螺纹总长的1/2。从引信内、外螺纹零件加工工艺看，即使两端止规进入，进入部分的螺纹尺寸也不会偏离最小实体状态很多，并且内、外螺纹两端偏离最小实体状态的部分在旋合后基本上是对应在一起的，因此可以假设螺纹有效长度为螺纹总长的2/3。

引信常用连接螺纹一般为中等旋合长度，如表3第1、2、3列所列。综合螺纹倒角、崩落和检验时对引信螺纹的要求，可得考虑了上述工艺因素影响后的引信螺纹各种有效长度如表3第4、5、6列所列。

(9)

(10)

(11)

系数kτ、kσ和kσw即反映了螺纹应力与螺纹直径d、螺距P、连接长度l的关系。

表3第7、8列分别为按表1确定的螺纹牙载荷不均系数kz，第9、10、11列分别为系数kτ、kσ和kσw的值。表中+∞代表极限情况下有效螺纹长度为负值，不能满足强度要求。

表3 第一系列的公称直径和螺距组合时螺纹剪切应力、挤压应力和弯曲应力的系数

续表

螺纹旋合长度l0/mm螺纹公称直径d/mm螺距P/mm螺纹去倒角后螺纹有效长度l1/mm螺纹去除倒角和崩落后的有效长度l2/mm螺纹除去倒角、崩落和1/3无效长度后的有效长度l/mm内、外螺纹材料均为钢时kz内螺纹材料为铝合金、外螺纹材料为钢时kz剪切应力系数kτ挤压应力系数kσ弯曲应力系数kσw7．58101216202430360．757．5-1．082P7．5-2．082P5-2．082P0．5600．7500．01470．02250．02761．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．01800．02700．03380．757．5-1．082P7．5-2．082P5-2．082P0．5600．7500．01140．01780．02161．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．01400．02130．02621．257．5-1．082P7．5-2．082P5-2．082P0．6250．7500．01750．02630．0329特0．757．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00940．01470．01771．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．01130．01750．02141．257．5-1．082P7．5-2．082P5-2．082P0．5600．7500．01420．02160．0267特0．757．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00680．01090．01311．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00830．01300．01561．507．5-1．082P7．5-2．082P5-2．082P0．5600．7500．01340．02060．0253特0．757．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00550．00870．01031．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00650．01030．01231．507．5-1．082P7．5-2．082P5-2．082P0．5600．7500．01050．01630．01982．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．02440．03720．0458特0．757．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00440．00720．00851．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00540．00850．01021．507．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00860．01350．01622．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．01990．03070．0374特0．757．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00350．00570．00681．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00420．00680．00801．507．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00670．01070．01282．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．01560．02430．0293特0．757．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00290．00480．0056特1．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00140．00220．00261．507．5-1．082P7．5-2．082P5-2．082P0．5600．7500．00560．00890．01052．007．5-1．082P7．5-2．082P5-2．082P0．5600．7500．01280．02010．02413．007．5-1．082P7．5-2．082P5-2．082P0．5600．750+∞+∞+∞

由表3可知，当螺纹旋合长度为5 mm和7.5 mm时，螺纹除去倒角、崩落和1/3无效长度后有效长度的极限范围分别为0.207～1.769 mm和0.836～2.439 mm，此时对应工作时的有效扣数范围分别为0.138～2.358和0.418～4.585。

3 结论和建议

本文提出了考虑到引信连接螺纹端头倒角、允许崩落长度和允许止量规适当进入等情形时引信内腔封口螺纹连接强度的计算方法。该方法在分析螺纹牙所受应力时仅需考虑与螺纹直径、螺距和连接长度相关的应力系数，使得计算过程简洁方便，计算结果准确可靠。结果表明：

1)螺距对螺纹强度影响较为敏感。在圈数足够多时，一般对于螺纹连接，当连接长度达到一定条件时，受冲击时实际有效扣数不会随啮合长度线性增长，此时采用大螺距或许更有利于提高强度。但是，一般情况下引信螺纹连接可以实现的有效扣数很少，在此情况下不考虑螺纹制造误差，连接长度一定且有限的情况下，尽可能选用较小螺距有利于提高强度。因此设计时在保证不发生“咬死”的前提下和旋合长度为中等旋合长度时应尽可能选用细牙螺纹甚至是比标准细牙还要小的特殊螺距如0.75。

2)在具体型号产品设计时，如果引信内腔封口连接螺纹强度受尺寸和材料限定难以满足发射(跌落)和隔爆安全性要求，则在设计时应尽可能减小内、外螺纹端头倒角、在技术要求中尽可能限制崩落长度以及止螺纹环规和止光滑量规的进入量。

3)《引信设计手册》和GJB/Z 135—2002《引信工程设计手册》给出的校核引信连接螺纹强度规范沿用了前苏联约70年前基于刚体力学假设的设计体系，仅针对剪切应力和挤压应力，既未考虑比挤压应力约大16%的弯曲应力，也未考虑到螺纹牙受力不均的情况，还未考虑通用制造规范允许的崩落和止规适当进入的放宽检验情形，因而计算结果是过于冒进的，相当于应力只考虑了不到50%。在此情况下之所以尚未大面积发现有引信内腔封口连接螺纹强度不足导致的失效现象，很可能与大多数引信内腔封口连接螺纹直径较大、连接螺纹长度与传爆管高度相关故强度设计的安全系数较大以及引信体和传爆管壳(或其他引信内腔封口连接螺纹本体零件)材料在一次性冲击载荷作用下的强度可能会有所提高有关。

4)螺纹牙所受弯曲应力恒大于挤压应力，且挤压许用应力恒大于弯曲许用应力，因此在进行强度校核时仅需校核弯曲强度和剪切强度即可。

5)剪切应力接近弯曲应力的二分之一(46.6%)，此规律可作为螺纹连接强度设计计算结果校验参考。

很少见有文献给出螺纹牙的材料许用应力和安全系数选取指南。从数种型号引信设计实践看，文献[7]和[8]给出的螺纹材料许用应力范围可能偏于保守，并不适应一次性冲击加载而内部空间限制又非常严格的引信，有必要根据制式型号产品通过反求工程学等方法进行系统、深入研究。

[1]曲萍. 阀体和阀盖连接螺纹螺距的选择[J].阀门，2011(2)：22-25.

[2]段巍，温新林，唐贵基，等. 不同旋合扣数下钢拉杆螺纹联接强度试验及有限元应力分析[J].机械强度，2008,30(5)：823-828.

[3]安晓卫，李丽，刘修亚. 基于有限元子模型的特种容器螺纹强度分析[J].机械强度，2013,35(6)：816-822.

[4]倪庆杰，曹成壮，孙勇，等. 解决底排火箭增程弹战斗部与发动机连接强度技术关键[J].弹箭与制导学报，2015,35(2):150-153.

[5]杨国麟. 对小口径弹全保险型引信底部内螺纹强度设计准则的探讨[J].兵工学报(引信分册)，1981(1)：18-25.

[6]高峰，王雨时. 引信隔爆试验内腔气体压力的工程计算[J].南京理工大学学报，2007,31(5)：546-549.

[7]徐灝主编. 机械设计手册(第2版)[M]. 北京：机械工业出版社，2000.

[8]郭可谦，杨育中，佘公藩. 紧固件连接设计手册[M]. 北京：国防工业出版社，1990.

[9]谭中刚，王新波，曾玉铭，等. MJ螺纹强度理论与计算[M]. 西安：西北工业大学出版社，2014.

[10]GJB/Z135-2002引信工程设计手册[S]. 北京：国家军用标准出版发行部，2003.

[11]《引信设计手册》编写组. 引信设计手册[M]. 北京：国防工业出版社，1978:104.

[12]BACИJIБEBMФ. 点火信管和起爆信管的设计原理[M]. 安克刚，倪明谦，译. 哈尔滨：中国人民解放军军事工程学院，1955.

[13]GB/T3-1997普通螺纹 收尾、肩距、退刀槽和倒角[S]. 北京：中国标准出版社，1997.

[14]WJ241-1965引信制造与验收技术条件[S]. 北京：中华人民共和国第五机械工业部，1971.

[15]GJB166-1986引信制造与验收技术条件[S]. 北京：国家军用标准出版发行部，1987.

本 刊 声 明

本刊编辑部

Influence of Screw Pitch to Joint Strength of Fuze Inner Cavity Sealing Thread

YIN Zhen, WEN Quan, WANG Yushi, ZHANG Zhibiao

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)

In the view of the strength design and especially pitch optimization of fuze inner cavity sealing connection thread, the stress calculation formulas of thread that appeared in the mechanical design theory was derived. Considered the end chamfering, allowed caving length and check gauge appropriate to enter, a new computing method was proposed. The stress counting process could much convenient and the more reliable results would achieved than before by using this method. Results showed that the strength of thread are greatly affected by pitch, when screw manufacturing error was ignored and connect length was limited, it is helpful to increase the thread strength by choosing little pitch as far as possible. It is unnecessary to check compression strength when strength checking, just bending strength and shear strength should be considered, it was found that the shear strength is close to half of the bending strength for crew tooth. Due to the bending strength, uneven loading factor of screw tooth, allowed caving length and check gauge appropriate to enter that stated in the general manufacturing specifications for fuze was not considered, the calculation results was too aggressive.

fuze; thread; screw pitch; stress analysis; joint strength

2016-09-11

殷瑱(1990—)，男，湖北广水人，硕士研究生，研究方向：特种机械技术。E-mail：yznjust@163.com。

TJ43

A

1008-1194(2017)01-0036-06

发起设立的“学术不端文献检测中心”,其功能是以《中国学术文献

总库》和大量国际学术文献为全文比对资源,辅助检查抄袭、一稿多投、不当署名、伪造、篡改等学术不端行为。我刊作为中国知网的合作单位,有义务为净化学术空气,制止学术不端行为作出贡献,请各位读者、作者大力支持,与我们共同努力,从根本上铲除学术腐败的土壤,树立全民求真、求实的科学态度。