航空飞行器轨迹引导逆次优控制算法

黄 伟，徐建城，吴华兴

(1.西北工业大学电子信息学院，陕西 西安 710072; 2.空军工程大学航空航天工程学院，陕西 西安 710038)

航空飞行器轨迹引导逆次优控制算法

黄 伟1，徐建城1，吴华兴2

(1.西北工业大学电子信息学院，陕西 西安 710072; 2.空军工程大学航空航天工程学院，陕西 西安 710038)

针对目前航空飞行器轨迹引导算法仅适用于特定引导过程，且未考虑系统动态性能要求的问题，提出了航空飞行器轨迹引导逆次优控制算法。该方法通过建立飞行器与目标相对运动的数学模型，以引导准确性和控制经济性为性能指标，根据系统动态性能要求计算时变权值系数，逆向得出线性反馈控制器，从而得到具有给定动态性能的次优引导系统。应用实例表明，该算法适用于包含多约束条件的航空飞行器引导过程，所得到的逆次优控制器满足引导准确性、控制经济性和系统动态性能等指标要求。

航空飞行器；引导系统；逆次优控制；动态特性

0 引言

航空飞行器引导技术是衡量航空领域发展水平的重要标志。随着飞行器性能的不断提升及作战任务的多样化，为发挥其最大的作战效能，对引导的准确性、控制的经济性以及所建立的引导系统的动态性能要求越来越高。建立具有普适性并易于工程化的引导算法，满足不同航空飞行器的作战使用要求，具有重要的现实意义。

以引导准确性和控制经济性为性能指标的航空飞行器引导过程是多约束条件下的优化问题，所建立的闭环引导系统必须满足一定的动态性能指标要求[1]。国内外相关学者对该问题进行了深入研究，文献[2]以引导时间为性能指标，建立了战斗机远距引导算法，但所得到的时间最优引导律缺乏普适性；文献[3]应用滑模技术得到了适用于跟踪机动目标的导弹制导律，但终端约束仅包含弹目相对速度，不能保证攻击的准确性；文献[4—6]针对战斗机近距引导过程，提出了多约束条件下的最优引导律，但所得到的控制器与性能指标的匹配性缺乏理论支撑，且未考虑系统动态性能要求；文献[7]基于引导过程特点提出一种非线性最优制导律，但其推导繁琐、计算耗时长，工程实现困难。由此可见，该领域研究现状所涉及的主要问题是：所提出的引导算法只适用于特定的引导过程，基于算法所得到的引导系统不具备给定的动态特性，实用性不强，工程实现困难。解决该问题的主要技术难点包括：如何建立满足一般引导过程的系统状态方程和性能指标函数；如何在难以准确估计结束控制时刻的前提下，保证所得到的控制器与性能指标的匹配性；如何使所得到的引导系统满足给定的动态性能指标要求。针对上述问题，提出了航空飞行器轨迹引导逆次优控制算法。

1 状态方程与性能指标函数

1.1 状态方程的建立

建立满足一般引导过程的系统状态方程是飞行器引导系统设计的基础。假设飞行器(战斗机、导弹)各控制通道互不影响，仅在水平平面内研究飞行器的引导过程，飞行器与目标的相对运动关系如图1所示。

图1中，飞行器位于O点，目标位于M点，目标速度矢量水平分量为Vm，φm和θm分别为水平面内目标速度前置角和航向角，V为飞行器速度矢量水平分量，φ和θ分别为水平面内飞行器速度前置角和航向角，ε为目标线角。将速度矢量Vm和V投影到目标线LOS及其法线上可得[5]

(1)

(2)

(3)

飞行器和目标的加速度在目标线法线上的分量分别为

(4)

(5)

由式(3)—式(5)可得

(6)

式(6)即为飞行器与目标在水平面内相对运动关系的数学模型。将飞行器和目标在目标线法线上的加速度作为引导系统的控制量和干扰量，并假设目标不做机动(jm=0)，考虑到飞行器角度关系式φ=ε-θ，可得系统状态方程为：

(7)

1.2 性能指标函数的建立

性能指标函数的建立是飞行器引导系统设计的难点，不同的引导过程所要求的性能指标不同，不同的引导阶段性能指标的侧重点也不相同。一般情况下，性能指标函数中包含多个约束条件。下面以战斗机近距引导和SAR(Synthetic Aperture Radar, SAR)制导导弹末制导过程为例，说明建立性能指标函数过程中应着重考虑的因素。

战斗机近距引导过程中，使用单一目标线角速度约束的比例导引法和单一前置角约束的最佳前置法并不能保证引导的准确性[5]，原因在于：引导初始阶段，战斗机与目标距离较远，目标线角速度数值非常小，以至于现有的测量手段无法量测，并且较小的目标线角速度误差将可能产生较大的引导误差，由此，必须对前置角加以约束，这不仅可以保证引导初始阶段的准确性，还可以使战斗机在引导结束时刻，相对目标取得一定的角度占位优势，有利于形成武器发射条件；对于近距引导结束阶段，为了将战斗机准确地引导至目标附近，必须对目标线角速度加以约束，以确保引导精度。所以，战斗机近距引导过程中性能指标的选取应综合考虑目标线角速度误差和前置角度误差。

SAR导引头末制导过程中，由于SAR自身的特点，为了获得所需的方位向分辨率，导弹飞行速度矢量方向与目标线必须保持一定的前置角。此外，为了保证引导的准确性，分析脱靶量可知，结束控制时刻目标线角速度应趋于零[8]。由此可见，SAR制导导弹末制导同战斗机近距引导的性能指标形式相同，都包含对目标线角速度误差和前置角度误差的约束，不同之处在于：战斗机近距引导的理想前置角是根据目标线和前置点计算得到，而SAR末制导理想前置角则根据成像所需方位向分辨率计算得到。通过上述分析，可建立航空飞行器一般引导过程的二次型性能指标函数

(8)

式(8)中，φ、ω、j分别为飞行器前置角、目标线角速度、法线加速度，φT、ωT分别为飞行器理想前置角及理想目标线角速度，q11、q22、r均为权值系数，tk为结束控制时刻。应该注意到，以前置角误差和目标线角速度误差作为终端约束条件，并考虑控制经济性的性能指标函数仅适用于一般引导过程，实际应用过程中，可根据作战使用的具体要求和飞行器自身特点建立相应的性能指标函数。

2 轨迹引导逆次优控制算法

通过上述分析可知，引导最优问题具有以下特点：1) 状态方程是一阶线性时变的，时变系数基于引导过程中传感器的量测；2) 由于目标运动的随机性，结束控制时刻难以准确估计；3) 闭环引导系统应具有给定的动态性能。根据以上特点，提出一种逆次优引导控制算法，该算法基于式(7)所表示的状态方程和式(8)所表示的性能指标函数，结合系统动态性能的具体指标要求，计算性能指标函数中的待定权值系数，逆向得出次优线性反馈控制器，从而使所建立的引导系统满足引导的准确性、控制的经济性，以及系统动态性能等指标要求。

将式(7)和式(8)转化为标准形式

(9)

(10)

式(10)中，R(t)和Q(t)均为待定的性能指标权值矩阵。不难证明，式(9)表示的系统状态方程是能控的，根据最优控制理论，最优控制量为：

U(t)=-R-1(t)BT(t)P(t)ΔX(t)

(11)

P(t)满足黎卡提方程及边值条件

P(t)B(t)R-1(t)BT(t)P(t)P(tk)=Q(t)

(12)

显然，当P(t)对称的情况下，若状态变量维数为n，黎卡提方程包含n(n+1)/2个独立的非线性微分方程，在理想条件下求解已十分困难，加之引导过程中飞行器与目标运动状态的剧烈变化，结束控制时刻tk的估计算法复杂[9-10]，且存在较大的估计误差，这将进一步增加黎卡提方程求解的复杂性。为满足工程化需求，针对这一问题文献[11]指出：由于引导过程的每一时刻t都可能对应结束时刻tk，即t→tk，P(t)存在稳态解[11]

(13)

式(13)表示的P(t)求解方法给工程应用带来了极大的方便，所得到的控制量理论上是次优的，但从作战使用和工程实现角度考虑，则是最优的。将式(13)代入式(11)，可得次优控制量为：

U(t)=-R-1(t)BT(t)Q(t)ΔX(t)

(14)

式(14)所表达的次优控制量取决于权值矩阵R(t)和Q(t)所包含元素的比值，与元素的绝对数值无关。由此，令R(t)=I为单位阵。假设飞行器飞行控制系统无迟滞的响应式(14)，将式(14)代入式(9)，次优闭环引导系统状态方程为：

+B(t)BT(t)Q(t)XT(t)

(15)

式(15)中，XT(t)=X(t)+ΔX(t)为理想状态变量。假设引导过程中所有运动参数的量测都准确理想，则A(t)和B(t)为已知。接下来将根据闭环引导系统给定的动态性能指标计算Q(t)，对于简单系统，若给定动态系统调节时间ts，通过对式(15)两端积分可计算得到Q(t)；对于慢变系数的复杂系统，特征值对系统动态性能具有主导作用，通过给定的系统特征值λi，可建立式(16)所表达的特征方程求解得出Q(t)。

det[λiI-A(t)+B(t)BT(t)Q(t)]=0

(16)

应该注意到，根据系统不同的动态性能指标要求，求解Q(t)的方法是多样的，所得到的Q(t)是随引导过程时变的。将Q(t)代入式(14)，可得次优反馈控制量，进而得到具有给定动态性能的次优引导系统。如果所得到的次优控制量超出限制条件，即U(t)>Umax，则在容许区间内调整系统动态性能指标的给定值，重新计算Q(t)，所涉及的参数寻优算法较为成熟。

上述的逆次优控制算法适用于包含多约束条件的航空飞行器引导过程，所得到的逆次优控制器综合考虑了引导准确性、控制经济性和系统动态性能等指标要求。由于权值矩阵Q(t)同时包含在控制量和性能指标函数中，对于不同的系统动态性能指标要求所带来的Q(t)的变化，并不会影响控制量对于性能指标的最优性，保证了控制器与性能指标的匹配性。

3 算法应用实例

下面以空空主动雷达弹末制导过程为例，验证本文提出的逆次优引导控制算法的有效性。在不考虑雷达导引头动力学误差及随机误差的基础上，假设末制导过程中目标始终处于导引头探测范围之内，对导弹前置角无约束，性能指标仅考虑脱靶量及控制经济性，控制量为飞行器水平面内目标线法向加速度。根据式(7)和式(8)建立水平面内状态方程及性能指标函数分别为：

(17)

(18)

其中，q和r均为时变权值系数，为保证制导的准确性，有效减小脱靶量，式(18)中的理想目标线角速度ωT=0。根据逆次优控制算法，结合式(13)和式(14)可得次优控制量为

(19)

由于控制量j与比值q/r有关，令r=1。假设导弹自动驾驶仪无迟滞的响应式(19)的指令加速度。将式(19)代入式(17)，可得闭环引导系统状态方程为

(20)

(21)

由式(21)可得

(22)

(23)

(24)

式(24)所得到的次优控制量与弹目初始距离R0、结束控制距离Rk、弹目径向速度V及目标线角速度ω有关，与比例导引法j=NVω形式相同，不同之处在于比例系数的选取，称为修正比例导引法。由此可知，比例导引作为最优制导律的典型代表[12]，理论上也是次优的。在实际应用过程中，修正比例导引法需要在导弹发射前装订R0及Rk，若R0≫Rk，可简化为j=3Vω。

下面对修正比例导引法进行仿真验证，水平面内导弹初始位置坐标(0,0)，初始速度为υx=0.5 km/s、υy=-0.5 km/s，导弹极限过载nmax=8，Rk=0.2 km时结束控制，导弹脱靶量h=10 m。目标初始位置坐标(20 km,5 km)，初始速度为υxt=-0.3 km/s、υyt=0 km/s，仿真中目标做过载恒定的侧向S机动，航向角不断减小。

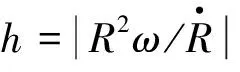
4 结论

本文提出了航空飞行器轨迹引导逆次优控制算法，该算法通过建立飞行器与目标相对运动的数学模型，以引导准确性和控制经济性为性能指标，根据系统动态性能要求计算时变权值系数，逆向得出线性反馈控制器，从而得到具有给定动态性能的次优引导系统。应用实例表明，该算法适用于包含多约束条件的航空飞行器引导过程，所得到的逆次优控制器保证了引导准确性、控制经济性和系统动态性能等指标要求，对于航空飞行器引导系统的综合与设计具有一定的理论参考价值。

[1]WeissH,HexnerG.Stabilityofmodernguidancelawwithmodelmismatch[C]//ProceedingsofAmericanControlConferenceBoston,Massachusetts.AACC2004: 3634-3639.

[2]韩庆,魏贤智,张斌,等.远距引导战斗机自动攻击控制律实现[J].电光与控制,2012,19(6):36-40.

[3]余家祥,杨秀庭,郭锐,等.基于滑模技术的舰舰导弹导引律设计[J].探测与控制学报,2003,25(2):23-27.

[4]WattsDJ,StrogatzSH.Collectivedynamicsof'SmallWorld'networks[J].Nature, 1998,393(6684):440-442.

[5]于雷,李言俊,欧建军.现代战机最佳引导算法研究[J].航空学报,2006,27(2):314-317.

[6]陈中起,张斌,杜永伟,等.近距引导战斗机自动攻击控制律实现[J].火力与指挥控制,2012,37(5):148-151.

[7]俞利新,欧向阳,欧建军,等.空对面导弹导引算法研究[J].弹箭与制导学报,2004,24(3):268-270.

[8]郭建国, 周军. 基于Nussbaum-type增益技术的末制导律设计[J]. 西北工业大学学报, 2010, 28(5): 753-757.

[9]LeeYI,KimSH,TahkMJ.Optimalityoflineartime-varyingguidanceforimpactanglecontrol[J].IEEETransactionsonAerospaceandElectronicSystems, 2012, 48(3): 2802-2817.

[10]RyooCK,ChoH,TahkMJ.Time-to-goweightedoptimalguidancewithimpactangleconstraints[J].IEEETransactionsonControlSystemsTechnology, 2006, 14(3): 483-492.

[11]KhannaSK,MailerK.Aeronauticalradiocontrolsystem[M].Moscow:RadioTechnologyPress, 2003: 65-81.

[12]王辉, 王江, 郭涛, 等. 基于逆最优问题的最优制导律及特性分析[J]. 固体火箭技术, 2014, 37(5): 587-593.

Inverse Suboptimal Control Algorithm for Trajectory Guidance of Aerial Vehicle

HUANG Wei1, XU Jiancheng1, WU Huaxing2

(1.Electronic and Information College, Northwestern Polytechnic University, Xi’an 710072,China; 2.Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China)

Traditonal algorithm for trajectory guidance of aerial vehicle is only available to certain guidance process. Regardless of system dynamic performance, an inverse suboptimal control algorithm for trajectory guidance of aerial vehicle was proposed. By modeling relative motion between vehicle and target, using guidance accuracy and control economy as metrics, time-varying weight coefficient were calculated on the basis of system dynamic performance, and linear feedback controller was derived inversely, thus suboptimal guidance system with dynamic performance was built. An application case showed that the algorithm could be applied to guidance processes including multi-constraints and the derived suboptimal controller fulfilled the requirements of accuracy, economy and dynamic performance.

aero vehicle; guidance system; inverse suboptimal control; dynamic performance

2016-07-02

国家自然科学基金项目资助(61472441)

黄伟(1980—)，男，黑龙江绥化人，博士研究生，副教授，研究方向：航空武器总体设计。E-mail：huangwei800519@163.com。

V249；TJ765.3

A

1008-1194(2017)01-0031-05