基于曼彻斯特编码特性的二次雷达混扰信号分选
2017-03-23刘垒,张玉,唐波
刘 垒,张 玉,唐 波
(解放军电子工程学院,安徽 合肥 230037)
基于曼彻斯特编码特性的二次雷达混扰信号分选
刘 垒,张 玉,唐 波
(解放军电子工程学院,安徽 合肥 230037)
针对二次监视雷达(SSR)应答信号混扰导致解码错误的问题,提出基于模式S应答信号曼彻斯特编码特性的SSR混扰信号分选算法。该算法首先根据曼彻斯特编码特性构建混扰信号的分选模型,将分选问题转化为非对称非正交的联合对角化问题,然后通过一种较为简洁的求解方法,快速求解出分离矩阵,以实现对混扰信号的有效分选,并可准确地估计出应答信号的到达方向。仿真验证表明,该算法在低信噪比情况下保持较好的分选性能,且其性能受应答信号的到达方向和相对延时影响较小。
二次雷达;信号分选;曼彻斯特编码;联合对角化
0 引言
二次监视雷达是空中交通管制系统的基础,可以通过询问、应答的方式获取飞机的距离方位、气压高度、飞机代码等重要信息[1-2]。SSR系统模式S是在传统的模式A/C基础上发展起来的,正逐步取代模式A/C,两种模式均遵循1 030 MHz的询问频率和1 090 MHz的应答频率。模式S应答信号采用曼彻斯特编码,且脉冲串的长度增加,具有较强的抗干扰能力和较大的信息量。随着空中交通流量的高速增长,电磁环境日益复杂,易产生多个应答机的应答信号相互混扰的现象,而传统的解码方法难以分辨这些在时域和频域相互重叠的信号,严重影响了信号的模式识别和解码[3],降低了SSR系统的安全性和可靠性。
目前国内外针对SSR混扰信号的分选问题提出了几种解决方案。P.Comon将其提出的独立成分分析(Independent Component Analysis, ICA)算法应用于SSR信号分选问题[4],然而SSR应答信号的高阶统计量已被证明为伪高斯性[5],因此任何基于峭度的分选算法都是非鲁棒的,分选失败率较高;N.Petrochilos提出了投影算法(Projection Algorithm, PA)[6],此算法可以巧妙地利用了信号的到达时间差,但当多个信号几乎同时到达时,此算法失效。文献[7]提出了基于多通道阵列处理的分选方法,首先通过旋转不变因子技术(Estimation of Signal Parameters via Rotational Invariance Techniques, ESPRIT),估计出应答机信号到达方向(DOA),再构建引导矩阵和分离矩阵,进行信号分离,但要求SSR接收机使用精确调整后的均匀线性阵列天线,存在一定的局限性;文献[8]提出了基于最小残量优化算法的分选方法,把优化问题转换为搜索问题,但由于搜索所需的定义域矩阵较大,运算量相对较大。目前较为有效的分选算法是N.Petrochilos提出的曼彻斯特解码算法(Manchester Decoding Algorithm, MDA)[9],此算法鲁棒性较好,但求解过程较为繁杂,运算量较大,且低信噪比下的分选成功率有待提高,分选得到的信号与原信号在幅值上有较大差异,易造成解码错误。本文针对此问题,提出了基于模式S应答信号曼彻斯特编码特性的SSR混扰信号分选算法。
1 应答信号特征及混扰模型
1.1 应答信号格式
模式S的应答信号具有四个前导脉冲(P1、P2、P3、P4)和一个应答数据块,如图1所示。每个前导脉冲的脉冲宽度为0.5 μs,应答数据块中包含56 bit或者112 bit的数据,数据采用曼彻斯特编码,即“01”表示数据“0”,“10”表示数据“1”。
脉冲串可表示为:
r=[1,0,1,0,0,0,0,1,0,1,0,0,0,0,0,0,r1,
r2,…,rn,…,rN]N=56 or 112
(1)
式(1)中,rn为应答信号码字,当数据为“0”时,rn=[01],当数据为“1”时,rn=[10]。
r的总长度为128或240,经脉冲幅度调制(Pulse Amplitude Modulation, PAM)后可表示为:
(2)
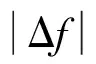
(3)
1.2 阵列信号混扰模型
假设天线阵元数为M,进入接收机的应答信号个数为K且K Y=AS+N (4) 应答信号矩阵S可表示为: R⊙Ψ (5) 式(5)中,⊙表示矩阵Hadamard积。 若询问机的接收天线采用均匀线性阵列天线,阵元间距为半波长,则阵列引导矢量ak为: k=1,2,…,K (6) 式(6)中,θk为应答信号sk相对于阵列法线的入射角度。 然而,在现实中引导矩阵A会受到多方面因素影响,如不精确的阵列天线刻度、天线耦合、阵列混扰等。因此,本文仅假设引导矩阵A为列满秩复矩阵,即仅要求阵元数大于信号源数。 为了实现信号的分选,需要找到一个分离矩阵W,得到应答信号S的估计值 (7) 1.3 曼彻斯特编码特性 模式S的应答信号采用曼彻斯特编码,则任意3个相邻的应答码字中至少有一个为0,所以积为0,即 (8) 同样,接收到的应答信号具有如下特性 (9) 2.1 混扰信号预处理 信源个数K可采用最小描述长度(Minimum Description Length, MDL)准则进行估计[10-11],该算法从信息论的角度出发,可对信源数进行有效估计,即 (10) 式(10)中,λi为样本协方差矩阵CY=1/LYYH的第i个大的特征值。 对观测到的混扰信号矩阵Y做奇异值分解(SVD)分解有 Y=UΛVH (11) 式(11)中,U∈M×M、V∈N×N均为酉矩阵;Λ=[ΛM0M×(N-M)],ΛM=diag(λ1,λ2,…,λM),λm(m=1,2,…,M)为混扰矩阵Y的奇异值,且排序为λ1≥λ2≥…≥λM。 令 定义 (12) 2.2 分选算法 (13) 由Kronecker积的性质,可得 (14) 定义 2≤n≤N-1 (15) 则有 (16) (17) 取VP的后K个列向量,则构成P零空间的一组基,即 (18) B0=W0R (19) 显然,对于B0的每一列有 (20) (21) (22) (23) 至此,将分选问题转化为联合对角化问题,求解式(23)的非对称非正交联合对角化问题即可求得分离矩阵W。 普通的对称正交联合对角化问题形如Ai=UΛiUH,其中U为酉矩阵,针对此类问题的常规求解方法主要有最小二乘算法[12]、Jacobi算法[13]、子空间算法[14]等。然而针对非对称非正交联合对角化问题的求解算法较少,文献[15]中提出了非对称最小二乘代价函数及三迭代算法(Triple Iterative Algorithm, TIA),但TIA算法每迭代一次需要交替更新三组待定的参数收敛速度较慢,运算量代价较大。 观察式(23)可以发现,我们感兴趣的待求变量只有矩阵W,而不需要精确求解矩阵Q和Λi,因此可以构造一种较为简洁的近似求解方法,以便快速求解分离矩阵W。 令 (24) 令E=C-1D,易得 (25) (26) (27) (28) 2.3 分选步骤 基于曼彻斯特编码特性的SSR混扰信号分选步骤如下: 第一步:通过MDL准则估计应答机个数; 第二步:对混扰信号矩阵Y做降维预处理得到Y′; 第三步:由Y′构建矩阵P; 第四步:对矩阵P做奇异值分解,求解其零空间的一组基B0; 第五步:求解非对称非正交联合对角化问题,得到分离矩阵W; 第七步:利用6 dB阈值法等方法解码; 影响算法分选效果的因素主要有信噪比、不同应答信号的DOA差值和信号延时,现分别从这几个影响因素出发将本文算法分选性能与ESPRIT算法、ICA算法和PA算法对比。假设天线阵元数为M=4,以2 MHz的采样率对下变频后的信号进行数字采样,考虑2个模式S应答信号发生混扰的情况,仿真结果均取1 000次独立蒙特卡罗实验的平均值。 3.1 分选过程仿真 固定两个信号的DOA为-2°和5°,相对延时为6 μs,信噪比为15 dB。图2为混扰前的原始应答信号。图3为噪声环境下的混扰信号,可见两个信号在时域上重叠,在t1到t2时间段内只存在信号s1,在t2到t3时间段内信号s1与s2重叠,在t3到t4时间段内只存在信号s2,如果直接对其解码会产生大量误码。图4为本文算法分选得到的两个应答信号,对比图2可见,两信号成功分离,解码后与原信号码元对比,计算出误码率为1.51%,通过式(28)计算得到DOA估计值为-1.901 2°和5.086 1°。 3.2 性能分析 首先固定两个信号的DOA为-2°和5°、相对延时为6 μs,信噪比从0 dB变化到30 dB。四种算法分选的误码率如图5所示。从图中可以直观地看出,信噪比低于18 dB时,本文算法误码率明显低于另外三种算法,在低信噪比情况下保持较好分选效果;信噪比大于18 dB后,四种算法误码率均趋于零,实现完全分离;ICA算法误码率最高,是因为SSR应答信号不完全满足ICA算法中的非高斯假设,易出现分选失败现象。四种算法DOA估计的均方根误差(Root Mean Squared Error, RMSE)比较如图6所示,可见,在DOA估计值方面本文算法与PA算法、ESPRIT算法性能相似,均可实现有效DOA估计,而ICA算法在此方面的性能仍表现最差。 接下来固定信噪比为15 dB、两信号相对延时为6 μs,且固定其中一个应答信号的DOA为-2°,另一个应答信号的DOA值相对变化,变化区间取0°至13°。四种算法分选的误码率如图7所示。易见,在DOA差值较小时,四种算法的分选性能均有所下降,但本文算法的分选性能受DOA差值影响相对较小;PA算法性能受DOA差值影响对大,在DOA差值较小时几乎失效,不能实现分选。 最后固定信噪比为15 dB、两个信号的DOA为-2°和5°,变化两应答信号的相对延时,变化区间取0~20 μs。四种算法分选的误码率如图8所示。可见,PA算法在相对延时较小时误码率较高,是因为PA算法利用两信号单独存在时的特征向量建立分离矩阵,当两信号延时较小时无法单独提取某一信号的特征向量,造成分选失败;ESPRIT算法和ICA算法的性能几乎不受相对延时影响;本文算法始终保持较低误码率,但随着相对延时增大误码率稍有增加,是因为此时零空间的基中包含了较多噪声等非信号自身因素特征,有待进一步优化。 本文提出了基于模式S应答信号曼彻斯特编码特性的SSR混扰信号分选算法。该算法将分选问题转化为非对称非正交的联合对角化问题,并通过一种较为简洁的求解方法,快速求解出分离矩阵,实现了对混扰信号的有效分选。仿真验证表明,该算法在低信噪比情况下保持较好的分选性能,且其性能受应答信号的到达方向和相对延时影响较小。当应答信号相对延时较大时,本文算法的误码率略有增加,此问题将在下一步的工作中研究解决。 [1]张尉. 二次雷达原理[M]. 北京: 国防工业出版社, 2009: 9-12. [2]王洪, 刘昌忠, 汪学刚. 二次雷达S模式综述[J]. 电讯技术, 2008, 48(7): 113-118. [3]Galati G,Bartolini S, Menè L. Analysis of SSR signals by super resolution algorithms[C]//Proceedings of the Fourth IEEE International Symposium on Signal Processing and Information Technology, Roma, 2004: 166-170. [4]Chaumette E, Comon P, Muller D. ICA-based technique for radiating sources estimation: application to airport surveillance[J]. IEE Proc.-F, 1993, 140(6):395-401. [5]Petrochilos N, Comon P. A zero-cumulant random variable and its applications[J]. Signal processing, 2006, 86(11): 3334-3338. [6]Petrochilos N, Galati G, Piracci E. Separation of SSR signals by array processing in multilateration systems[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(3): 965-982. [7]唐波, 程水英, 张浩. 基于多通道阵列处理的二次雷达混扰信号分选[J]. 电讯技术, 2014, 54(5): 534-540. [8]张玉, 樊斌斌, 胡进, 等. 基于最小残量优化算法的二次雷达信号分选[J]. 现代雷达, 2015, 37(4): 46-49+54. [9]Petrochilos N, Van der Veen A J. Algorithms to separate overlapping secondary surveillance radar replies[C]//IEEE International Conference on Acoustics Speech and Signal Processing (ICASSP). US: IEEE, 2004: 49-52. [10]Rissanen J. Modeling by shortest data description[J]. Automatica, 1978, 14(5): 465-471. [11]黄桂根, 孟兵, 李品. 一种基于MDL原理的信号分选新算法[J]. 数据采集与处理, 2015, 30(3): 656-668. [12]Belouchrani A, Abed-Meraim K, Cardoso J F, et al. A blind source separation technique using second-order statistics[J]. IEEE Transactions on Signal Processing, 1997, 45(2): 434-444. [13]Wax M,Sheinvald J. A least-squares approach to joint diagonalization[J]. IEEE Signal Processing Letters, 1997, 4(2): 52-53. [14]Yeredor A. Non-orthogonal joint diagonalization in the least-squares sense with application in blind source separation[J]. IEEE Transactions on Signal Processing, 2002, 50(7): 1545-1553. [15]Zhang H, Feng D, Nie W, et al. Non-orthogonal joint diagonalization for blind source separation[J]. Journal of Xidian University, 2008, 35(1): 27-31. [16]王洪, 刘昌忠, 汪学刚, 等. 强干扰背景下S模式解码方法[J]. 电子与信息学报, 2009, 31(12): 2876-2880. Garbled Secondary Surveillance Radar Echo SeparationBased on Manchester Encoding Property LIU Lei, ZHANG Yu, TANG Bo (Electronic Engineering Institute of PLA, Hefei 230037, China) In order to solve the decoding errors of secondary surveillance radar (SSR) due to the phenomenon of garble, an algorithm based on the manchester encoding property of mode S was proposed for separating the garbled replies. Firstly, a separation model was established on the basis of the manchester encoding property, so separation problem was transformed into a non-symmetrical non-orthogonal joint diagonalization problem. Then, a succinct method was proposed to solve for the separation matrix fast, and the direction of arrival (DOA) was estimated accurately. Numerical simulations show ed that the proposed algorithm maintained good separation performance in the low SNR case, and its performance was less affected by the DOA and relative delay. secondary surveillance radar; signal separation; Manchester encoding; joint diagonalization 2016-06-02 国家自然科学基金项目资助(61201379);安徽省自然科学基金项目资助(120805QF103) 刘垒(1990—),男,河北深州人,硕士研究生,研究方向:信号与信息处理。E-mail:songshiliulei@163.com。 TN958.96 A 1008-1194(2017)01-0020-06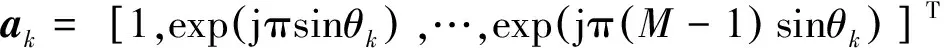
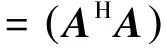
2 基于曼彻斯特编码特性的分选算法
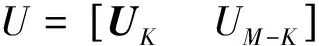
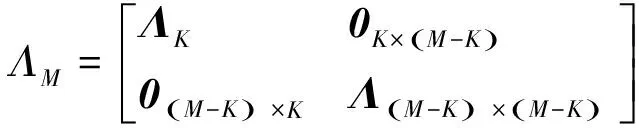
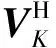
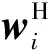
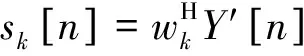
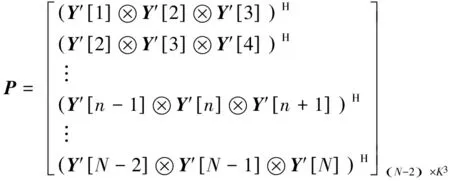
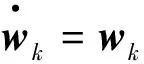
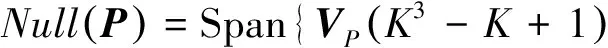
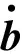
3 仿真分析
4 结论
